Bài 41 Trang 128 SGK Toán 9 Tập 1 – TopLoigiai

Trang chủ » Giải Bài 41 Trang 128 Sgk Toán 9 Tập 1 » Bài 41 Trang 128 SGK Toán 9 Tập 1 – TopLoigiai

Có thể bạn quan tâm

Mục lục nội dung Ôn tập chương IIBài Tập

Ôn tập chương II

Bài Tập

Bài 41 (trang 128 SGK Toán 9 Tập 1)

Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.

Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

b) Tứ giác AEHF là hình gì? Vì sao?

c) Chứng minh đẳng thức AE.AB = AF.AC

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

Lời giải:

Giải Toán 9: Bài 41 trang 128 SGK Toán 9 tập 1 – TopLoigiai

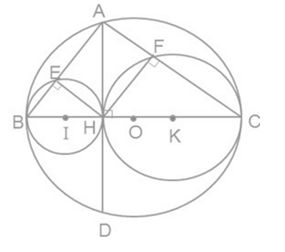
a)

IO = OB – IB => (I) tiếp xúc trong với (O).

OK = OC – KC => (K) tiếp xúc trong với (O)

IK = OH + KH => (I) tiếp xúc ngoài với (K)

Giải Toán 9: Bài 41 trang 128 SGK Toán 9 tập 1 – TopLoigiai

c) ΔAHB vuông nên AE.AB = AH2

ΔAHC vuông nên AF.AC = AH2

Suy ra AE.AB = AF.AC

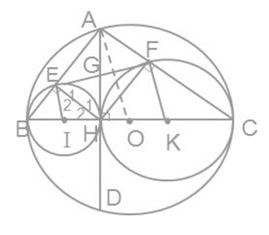
Giải Toán 9: Bài 41 trang 128 SGK Toán 9 tập 1 – TopLoigiai

e) - Cách 1:

Ta có: EF = AH ≤ OA (OA có độ dài không đổi)

Do đó EF lớn nhất khi AH = OA

<=> H trùng O hay dây AD đi qua O.

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.

- Cách 2: EF = AH = AD/2.

Do đó EF lớn nhất khi AD lớn nhất. Khi đó, dây AD là đường kính.

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.

Tham khảo toàn bộ: Giải Toán 9

Từ khóa » Giải Bài 41 Trang 128 Sgk Toán 9 Tập 1