Bài C6 Trang 118 SGK Vật Lí 9 - Vật Lý - Tìm đáp án, Giải Bài Tập, để

Đề bài

Vận dụng kiến thức hình học, hãy tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh trong hai trường hợp ở C5. Cho biết vật AB có chiều cao h = 1cm

Phương pháp giải - Xem chi tiết

Sử dụng tỉ số đồng dạng của các cặp tam giác đồng dạng.

Lời giải chi tiết

- TH1: Vật AB cách thấu kính một khoảng d = 36cm.

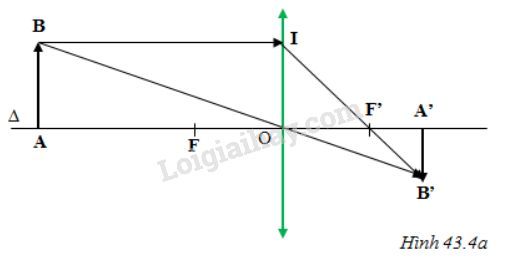
AB = h = 1cm

OA = d = 36cm

OF = OF' = f = 12cm

A'O = ? A'B' = ?

Ta có: \(\Delta OAB \sim \Delta OA'B' \Rightarrow {{A'B'} \over {AB}} = {{A'O} \over {AO}}\) (1)

Ta có: \(\Delta {\rm{OIF'}} \sim \Delta A'B'F' \Rightarrow {{A'B'} \over {OI}} = {{A'F'} \over {OF'}}\) (2)

Mà: OI = AB (3)

Từ (1), (2) và (3) \( \Rightarrow {{A'O} \over {AO}} = {{A'F'} \over {{\rm{OF}}'}} = {{A'O - {\rm{OF}}'} \over {{\rm{OF}}'}} \Leftrightarrow {{A'O} \over {36}} = {{A'O - 12} \over {12}}\)

\(\Rightarrow A'O = 18cm\)

Thay A’O = 18cm vào (1) ta có: \({{A'B'} \over 1} = {{18} \over {36}} \Rightarrow A'B' = 0,5cm\).

Vậy chiều cao của ảnh là 0,5cm, khoảng cách từ ảnh đến thấu kính là 18 cm.

- TH2: Vật AB cách thấu kính một khoảng d = 8cm.

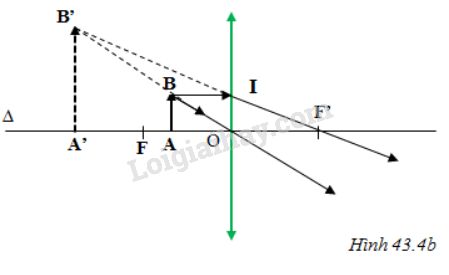
AB = h = 1cm

OA = d = 8cm

OF = OF' = f = 12cm

A'O = ? A'B' = ?

Ta có: \(\Delta OAB \sim \Delta OA'B' \Rightarrow {{A'B'} \over {AB}} = {{A'O} \over {AO}}\) (1)

Ta có: \(\Delta {\rm{OIF'}} \sim \Delta A'B'F' \Rightarrow {{A'B'} \over {OI}} = {{A'F'} \over {OF'}}\) (2)

Mà: OI = AB (3)

Từ (1), (2) và (3) \( \Rightarrow {{A'O} \over {AO}} = {{A'F'} \over {{\rm{OF}}'}} = {{A'O + {\rm{OF}}'} \over {{\rm{OF}}'}} \Leftrightarrow {{A'O} \over 8} = {{A'O + 12} \over {12}} \)

\(\Rightarrow A'O = 24cm\)

Thay A’O = 24cm vào (1) ta có: \({{A'B'} \over 1} = {{24} \over 8} \Rightarrow A'B' = 3cm\)

Vậy chiều cao của ảnh là 3cm, khoảng cách từ ảnh đến thấu kính là 24 cm.