Bài Tập Hàm Số Liên Tục Có Lời Giải- Đại Số Lớp 11 - TÀI LIỆU RẺ
Có thể bạn quan tâm
Tóm tắt tài liệu
- A. TÓM TẮT LÝ THUYẾT
- 1. Hàm số liên tục tại một điểm
- 2. Hàm số liên tục trên một khoảng, một đoạn
- 3. Tính chất hàm số liên tục
- B. BÀI TẬP HÀM SỐ LIÊN TỤC
- Dạng 1: Xét tính liên tục của hàm số tại một điểm, khoảng, đoạn
- Dạng 2: Xác định tham số để hàm số liên tục trên khoảng, đoạn.
- C. BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Bài tập hàm số liên tục là một dạng bài tập phổ biến thuộc chương giới hạn – Đại số lớp 11. Tài liệu dưới đây sẽ giúp các em hiểu rõ hơn về lý thuyết hàm số liên tục cũng như một số dạng bài tập đặc trưng nhất trong chuyên đề. Các em có thể tải tài liệu và in ra để tiện làm bài tập nhé. Chúc các em học tốt!
TẢI XUỐNG
A. TÓM TẮT LÝ THUYẾT
1. Hàm số liên tục tại một điểm
Hàm số liên tục: Giả sử hàm số \[y=f(x)\] xác định trên \[(a;b)\] và \[{{x}_{0}}\in (a;b)\]. Hàm số \[y=f(x)\] liên tục tại \[{{x}_{0}}\] \[\Leftrightarrow \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)=f({{x}_{0}})\]
Hàm số không liên tục tại \[{{x}_{0}}\] được gọi là gián đoạn tại \[{{x}_{0}}\]
2. Hàm số liên tục trên một khoảng, một đoạn
- Hàm số y = f(x) xác định trên khoảng (a;b). F(x) liên tục trên khoảng (a;b) khi và chỉ khi f(x) liên tục trên mọi điểm thuộc (a;b)
- Hàm số y = f(x) xác định trên đoạn [a;b]. f(x) liên tục trên khoảng (a;b) khi và chỉ khi f(x) liên tục trên khoảng [a;b] và lim bằng nhau khi x tiến đến a cộng hoặc a trừ.
- Chú ý: Các hàm số liên tục tại một điểm là hàm số liên tục tại điểm đó. Hàm sơ cấp bao gồm: Đa thức, phân thức, lượng giác liên tục trên từng khoảng xác định của chúng
3. Tính chất hàm số liên tục
Hàm số f(x) liên tục trên [a;b] và f(a) # f(b) => Với mọi M nằm giữa f(a) và f(b) tồn tại c thuộc (a;b) sao cho f(c) = M.
Hệ quả: Hàm số f(x) liên tục trên [a;b] và f(a).f(b) < 0; Tồn tại c thuộc (a;b) sao cho f(c) = 0.
Nhận xét:
Dùng hệ quả để chứng minh phương trình f(x) = 0 có ít nhất nghiệm trên khoảng (a;b)
Đồ thị hàm số liên tục là đường liền nét
B. BÀI TẬP HÀM SỐ LIÊN TỤC
Dạng 1: Xét tính liên tục của hàm số tại một điểm, khoảng, đoạn
Phương pháp giải: Sử dụng các công thức trong tài liệu. Ghi nhớ, sử dụng các phương pháp khử dạng vô định đã được học ở phần trước.




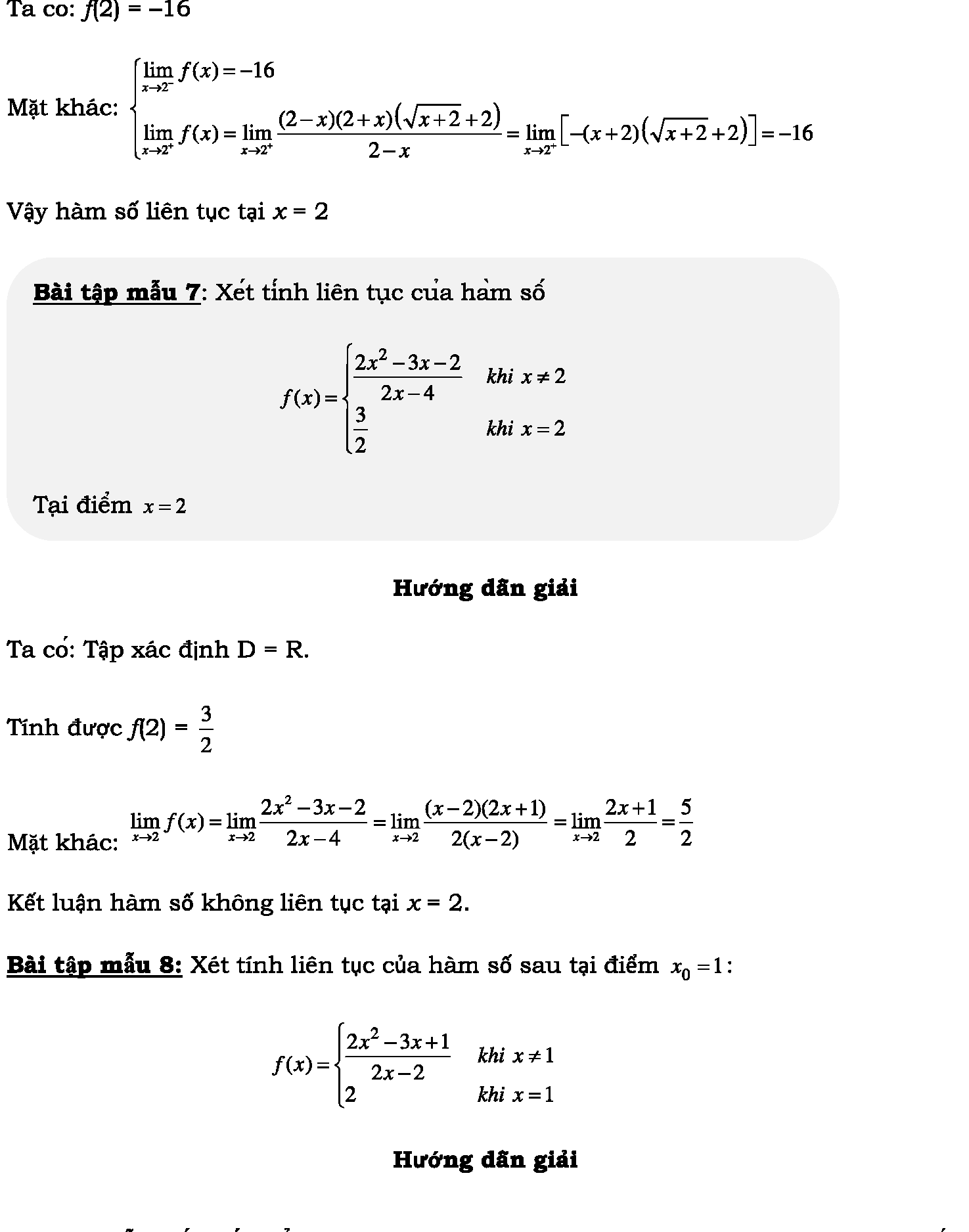




Dạng 2: Xác định tham số để hàm số liên tục trên khoảng, đoạn.
Phương pháp giải: Sử dụng các công thức trong tài liệu. Ghi nhớ, sử dụng các phương pháp khử dạng vô định đã được học ở phần trước.









C. BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Dưới đây là tổng hợp các bài tập trắc nghiệm liên quan đến hàm số liên tục







Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập hàm số liên tục. Mong rằng với những bài toán bên trên có thể giúp các em một phần chinh phục chuyên đề này. Để đạt được kết quả cao nhất trong quá trình học chương hàm số liên tục, các em cần nắm vững phần lý thuyết. Đây là điểm lý thuyết cực kì quan trọng, tạo nền tảng cho các em học chương trình toán 12 nói riêng, thi THPT quốc gia nói chung. Chúc các em học tốt!
Từ khóa » Bài Tập Lim Lớp 11 Có đáp án Tự Luận
-
Bài Tập Giới Hạn Vô Cực Lớp 11 Có đáp án - 123doc
-
Bài Tập Giới Hạn Hàm Số Có đáp án - Tài Liệu - 123doc
-
Lý Thuyết Và Bài Tập Chuyên đề Giới Hạn - Lư Sĩ Pháp
-
15 Dạng Bài Giới Hạn, Hàm Số Liên Tục Chọn Lọc, Có Lời Giải
-
Các Dạng Toán Về Giới Hạn Hàm Số Lớp 11 Có Lời Giải Chi Tiết
-
Bài Tập Có đáp án Chi Tiết Về Giới Hạn Của Hàm Số Lớp 11 Phần 28
-
Bài Tập Giới Hạn Dãy Số Năm 2020 Có đáp án Chi Tiết
-
Bài Tập Ôn Tập Chương 4 Giới Hạn Có Lời Giải (Tự Luận
-
Tổng Hợp Lý Thuyết Và Bài Tập Chuyên đề Giới Hạn
-
Bài Tập Giới Hạn Hàm Số - Môn Toán 11 – Thầy Nguyễn Công Chính
-
Đề Thi Học Kì 1 Lớp 11 Môn Toán Có Đáp Án Sở GD&ĐT Quảng Nam