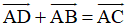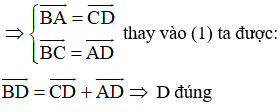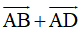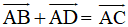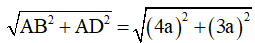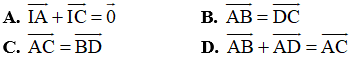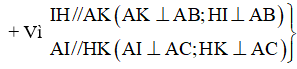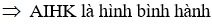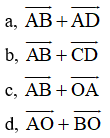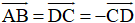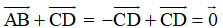Bài Tập Về Quy Tắc Hình Bình Hành Của Vecto ...

1. Lớp 10
2. Toán học

Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết

Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết 

1557 Tải tài liệu « Trang trước Chia sẻ Trang sau »

Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết

A. Phương pháp giải

Áp dụng quy tắc hình bình hành và các tính chất của hình hình hành đã học ở lớp 8 để giải bài tập.

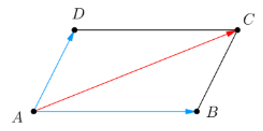
Quy tắc hình bình hành Nếu ABCD là hình bình hành thì ta có Quy tắc này cũng đúng nếu ta xuất từ các đỉnh khác của hình bình hành.

B. Ví dụ minh họa

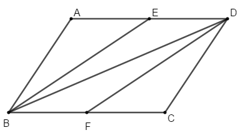
Ví dụ 1: Cho hình bình hành ABCD với E và F lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai?

Hướng dẫn giải:

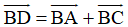
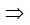
+ Ta có: ABCD là hình bình hành nên theo quy tắc hình bình hành ta được: (1) A đúng

+ Lại có: ABCD là hình bình hành

Ví dụ 2: Cho hình chữ nhật ABCD có AB = 4a và AD = 3a. Tính độ dài

Hướng dẫn giải:

ABCD là hình chữ nhật, suy ra ABCD cũng là hình bình hành, nên ta áp dụng quy tắc hình bình hành ta được:

Suy ra 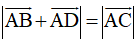= AC

Ta lại có: AC =

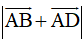
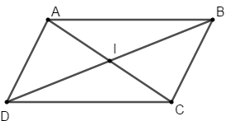
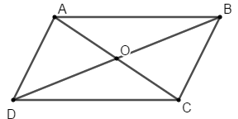
Vậy = 5a.

Ví dụ 3: Cho hình bình hành ABCD tâm I. Khẳng định nào sau đây là khẳng định sai?

Hướng dẫn giải:

+ Ta có I là tâm của hình bình hành ABCD nên I là trung điểm của AC

Do đó 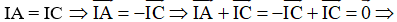đúng

+ Do ABCD là hình bình hành 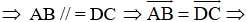đúng

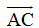
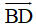
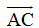
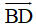
+ AC và BD là hai đường chéo của hình bình hành nên chúng cắt nhau, do đó hai vecto và không cùng phương nên vecto không thể bằng vecto (nhớ lại khái niệm hai vecto bằng nhau là cùng hướng và có độ dài bằng nhau) C sai

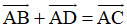
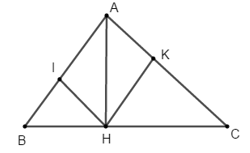
+ Ta có: theo quy tắc hình bình hành D đúng

Ví dụ 4: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I và K lần lượt là chân đường vuông góc hạ từ H lên AB và AC. Khẳng định nào sau đây là sai?

Hướng dẫn giải:

Ví dụ 5: Cho hình bình hành ABCD tâm O. Tính các vecto sau

Hướng dẫn giải:

a, 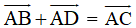theo quy tắc hình bình hành

b, Vì AB // CD nên ta có

Do đó:

c,

= (sử dụng tính chất giao hoán)

= (quy tắc ba điểm)

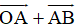
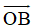
d,

Vì ABCD là hình bình hành tâm O nên O là trung điểm của AC

Suy ra AO = OC

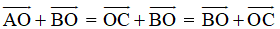
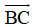
Ta có: (tính chất giao hoán)

= (quy tắc ba điểm)

1557 Tải tài liệu « Trang trước Chia sẻ Trang sau »

Nội dung bài viết

Xem thêm

Có thể bạn quan tâm

• Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo

• Giải sbt Tiếng Anh 10 Explore New Worlds – Cánh diều

• Trắc nghiệm Hóa học lớp 10 có đáp án - Chân trời sáng tạo

• Trắc nghiệm Hóa học lớp 10 có đáp án - Cánh diều

• Trắc nghiệm Hóa học lớp 10 có đáp án - Kết nối tri thức

• Trắc nghiệm Toán lớp 10 có đáp án - Chân trời sáng tạo

• Trắc nghiệm Toán lớp 10 có đáp án - Cánh diều

• Trắc nghiệm Toán lớp 10 có đáp án - Kết nối tri thức

• Giải sbt Tiếng Anh 10 Global Success – Kết nối tri thức

• Giải SBT Kinh tế pháp luật 10 – Chân trời sáng tạo

• Giải SBT Kinh tế pháp luật 10 – Cánh diều

• Giải SBT Kinh tế pháp luật 10 – Kết nối tri thức

• Giải SBT Địa lí 10 – Chân trời sáng tạo

• Giải SBT Địa lí 10 – Cánh diều

• Giải SBT Địa lí 10 – Kết nối tri thức

Thông báo

× × Trải nghiệm miễn phí Hỏi đáp với App VietJack ! Tiếp tục sử dụng web! Đăng nhập vào hệ thống × Tài khoản Google Lưu mật khẩu Bạn quên mật khẩu? Đăng nhập Bạn chưa có tài khoản? Đăng ký ngay Đăng ký vào hệ thống × Tài khoản Google Đăng ký Bạn đã có tài khoản? Đăng nhập ngay Khôi phục tài khoản × Khôi phục Bạn đã có tài khoản? Đăng nhập ngay Đặt câu hỏi