Bạn Biết Gì Về đường Thẳng Và đường Tròn Ơ-le (Euler)

Trang chủ » đường Thẳng Euler Là Gì » Bạn Biết Gì Về đường Thẳng Và đường Tròn Ơ-le (Euler)

Có thể bạn quan tâm

1. Đường thẳng Ơ-le (Euler) Trong một tam giác, trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác nằm trên một đường thẳng (gọi là đường thẳng Ơ-le). Chứng minh: Các điểm được đặt tên như hình vẽ:

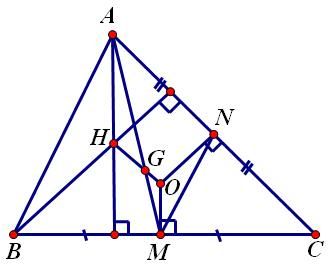
Ta có: ΔHAB∼ΔOMN(g.g) ⇒OMAH=12 Cơ mà GMGA=12⇒OMAH=GMGA Lại có: HAGˆ=GMOˆ AGHˆ=MGOˆ⇒H,G,O−−−−−− 2. Đường tròn Ơ-le (Euler) Trong một tam giác, chân 3 đường cao, 3 trung điểm 3 cạnh và 3 trung điểm các đoạn thẳng nối trực tâm đến đỉnh cùng nằm trên một đường tròn. Chứng minh: Đặt tên các điểm như hình vẽ.

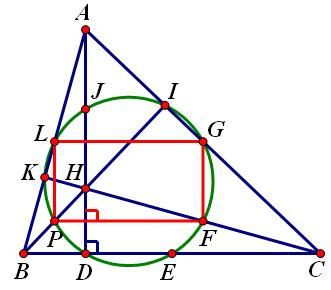Để ý thấy LGFP là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của LF và GP. (1) Tương tự: GIPD là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của IDvà GP(2) PEGJ là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của EJ và PG(3) EFJL là hình chữ nhật nên nội tiếp đường tròn có tâm là trung điểm của LF và EJ(4) Từ (1),(2),(3),(4) suy ra 9 điểm D,E,F,G,I,J,L,K,P nằm trên cùng 1 đường tròn. (đường tròn 9 điểm - đường tròn Ơ le)

Nhắn tin cho tác giả Toán Tiểu học @ 21:17 22/11/2014 Số lượt xem: 3922 Số lượt thích: 1 người (Hoàng Công Toại)

Từ khóa » đường Thẳng Euler Là Gì