Các Bước Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc 3
Có thể bạn quan tâm
A. Lý thuyết
I- SƠ ĐỒ CHUNG KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ.
1. Tập xác định.
2. Sự biến thiên
2.1 Xét chiều biến thiên của hàm số
+ Tính đạo hàm y’
+ Tìm các điểm mà tại đó đạo hàm y’ bằng 0 hoặc không xác định
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực (\(x\rightarrow \pm \infty\) ), các giới hạn có kết quả là vô cực và tìm tiệm cận nếu có.
2.4 Lập bảng biến thiên.
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
3. Đồ thị
- Giao của đồ thị với trục Oy: x=0 =>y= ? => (0;?)
- Giao của đồ thị với trục Ox: y = 0 <=> f(x) = 0 <=> x = ? => (?;0 )
- Các điểm CĐ; CT nếu có.
(Chú ý: nếu nghiệm bấm máy tính được thì bấm, nghiệm lẻ giải tay được thì phải giải ra- chẳng hạn phương trình bậc 2, còn nghiệm lẽ mà không giải được thì ghi ra giấy nháp cho biết giá trị để khi vẽ cho chính xác- không ghi trong bài- chẳng hạn hàm bậc 3)
- Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
- Nhận xét về đặc trưng của đồ thị. Điều này sẽ cụ thể hơn khi đi vẽ từng đồ thị hàm số.
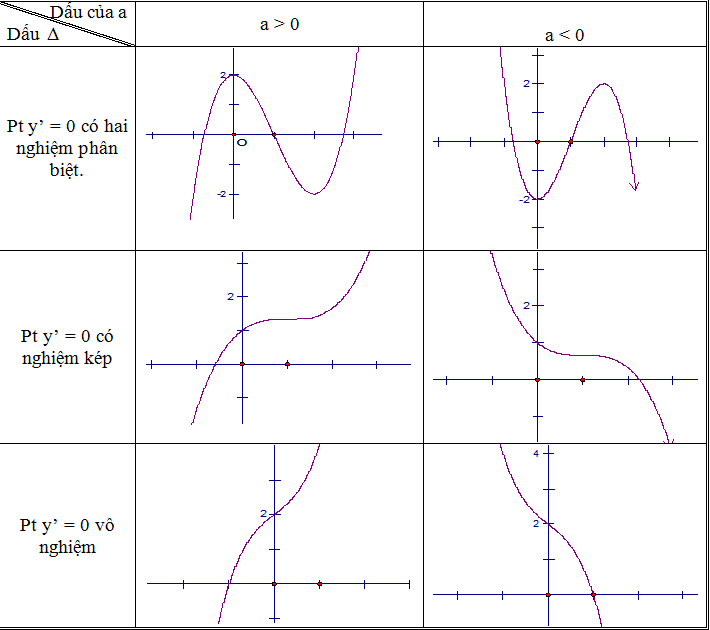
II- SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM BẬC BA: y = ax3 + bx2 + cx + d (a ¹ 0) .
1. Tập xác định. D=R
2. Sự biến thiên
2.1 Xét chiều biến thiên của hàm số
+ Tính đạo hàm:
+ ( Bấm máy tính nếu nghiệm chẵn, giải nếu nghiệm lẻ- không được ghi nghiệm gần đúng)
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực (\(x\rightarrow \pm \infty\))
(Hàm bậc ba và các hàm đa thức không có TCĐ và TCN.)
2.4 Lập bảng biến
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
3. Đồ thị
- Giao của đồ thị với trục Oy: x=0 =>y= d => (0; d)
- Giao của đồ thị với trục Ox: y = 0 <=> ax3 + bx2 + cx + d = 0 <=> x = ?
- Các điểm CĐ; CT nếu có.
(Chú ý: nếu nghiệm bấm máy tính được 3 nghiệm thì ta bấm máy tính, còn nếu được 1 nghiệm nguyên thì phải đưa về tích của một hàm bậc nhất và một hàm bậc hai để giải nghiệm. Trường hợp cả ba nghiệm đều lẻ thì chỉ ghi ra ở giấy nháp để phục vụ cho việc vẽ đồ thị)
- Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
- Nhận xét về đặc trưng của đồ thị. Hàm bậc ba nhận điểm làm tâm đối xứng.
+ Trong đó: x0 là nghiệm của phương trình y’’ = 0 (đạo hàm cấp hai bằng 0)
+ Điểm I được gọi là ‘điểm uốn’ của đồ thị hàm số.
Các dạng đồ thị hàm số bậc 3:y = ax3 + bx2 + cx + d (a ¹ 0)
B. Ví dụ minh họa
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số : y = x3 + 3x2 – 4
1. Tập xác định D = R
2. Sự biến thiên
+)Giới hạn hàm số tại vô cực
;
+)Chiều biến thiên:
y’ = 3x2 + 6x
Cho y’ = 0 <=> 3x2 + 6x = 0 <=> \(\left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\)
Hàm số đồng biến trong khoảng (-∞; -2) và (0; +∞)
Hàm số nghịch biến trong khoảng (-2; 0)
+) Cực trị
Hàm số đạt cực đại tại x = -2; \(y_{CD}=y(-2)=0\)
Hàm số đạt cực tiểu tại x = 0; \(y_{CT}=y(0) = -4\)
+)Lập bảng biến thiên :
| x | -∞ | -2 | 0 | +∞ |
| y’ | + | 0 – | 0 + | |
| y | -∞ | 0 | -4 | +∞ |
3. Đồ thị
Giao của đồ thị với trục Ox: y = 0 <=> x3 + 3x2 – 4 = 0 <=> \( (x-1)(x+2)^{2}=0\)
<=> \(\left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
Vậy (-2;0) và (1;0) là các giao điểm của đồ thị với trục Ox
Giao điểm của đồ thị với trục Oy: x = 0 <=> y = -4. Vậy (0;-4) là giao điểm của đồ thị với trục Oy.
Bảng giá trị :
| x | -2 | -1 | 0 | 1 |
| y | 0 | -2 | -4 | 0 |
Tìm điểm uốn
y’’= 6x + 6
Cho y’’ = 0 <=> 6x + 6 = 0 <=> x = -1 => y = -2
Đồ thị hàm số có điểm uốn : U(-1, -2)
Vẽ đồ thị (C) :
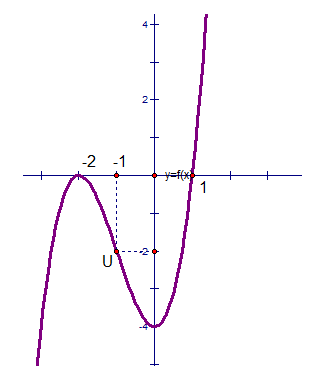
Kết luận: Đồ thị hàm số bậc 3 đã cho nhận điểm U(-1;-2) làm tâm đối xứng.
C. Một số bài tập trong đề thi đại học

![]()
D. Bài tập vận dụng
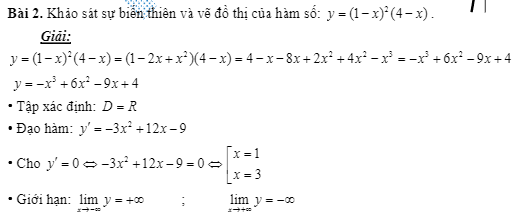
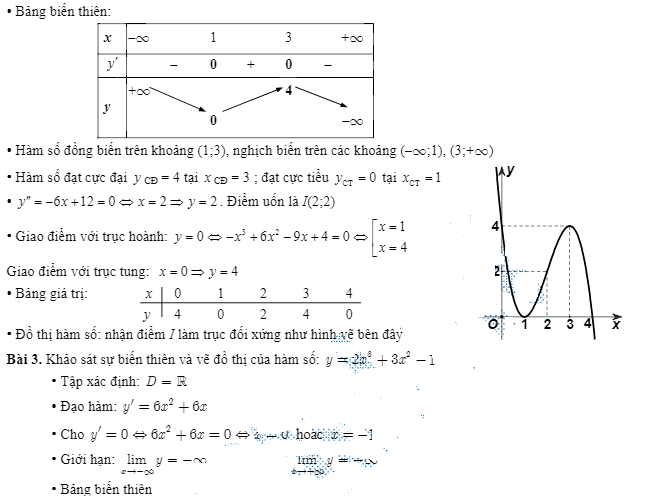
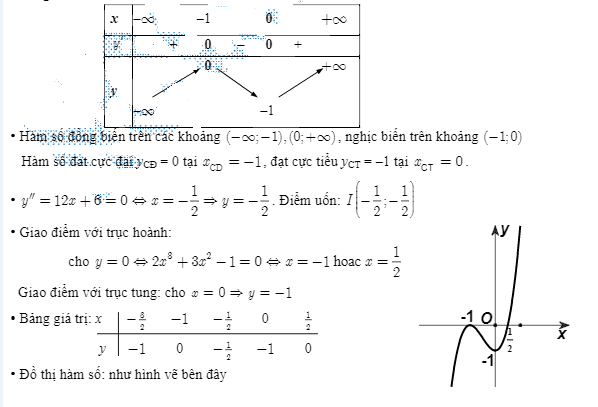

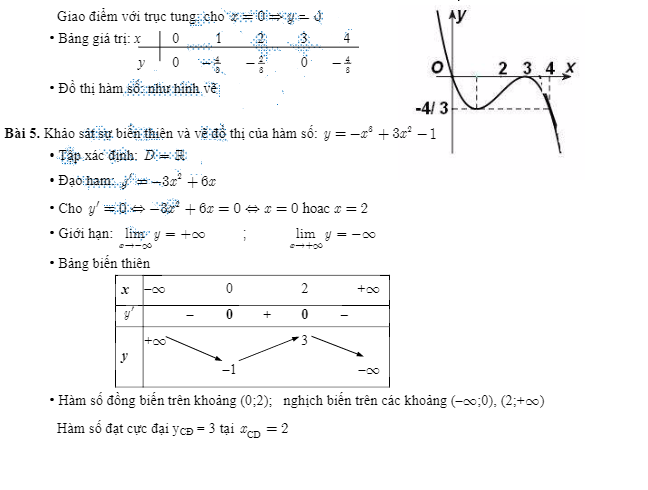
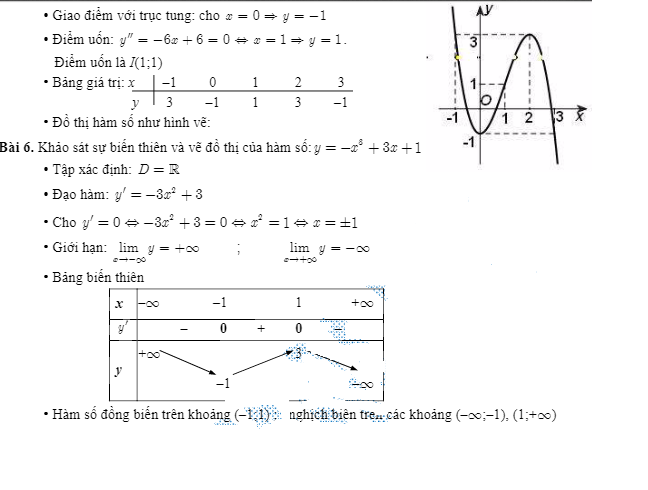
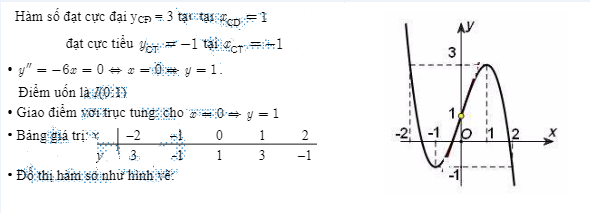
Bài tập về nhà

Từ khóa » Khảo Sát Hàm Số Bậc 3 Không Có Cực Trị
-
Ứng Dụng Đồ Thị Hàm Số Bậc 3 Vào Giải Toán - Kiến Guru
-
Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc Ba
-
Khảo Sát Hàm Số Bậc 3 Và đánh Giá Hệ Số Hàm Số Bậc 3
-
Khảo Sát Hàm Số Bậc 3 Không Có Cực Trị - 123doc
-
Tìm điều Kiện để Hàm Số Bậc 3 Có Cực Trị Thỏa Mãn điều Kiện Cho Trước
-
Khảo Sát Hàm Số Và Dạng đồ Thị Của Các Hàm Số
-
Chọn Kết Luận đúng: Hàm Số Bậc Ba Không Có Cực Trị Thì đồ Thị Cắt ...
-
Tìm M để Hàm Bậc Ba Không Có Cực Trị Cực Hay, Có Lời Giải - Toán Lớp ...
-
Các Dạng đồ Thị Của Hàm Số Bậc Ba, Bậc Bốn Trùng Phương - Mathvn
-
Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc Ba | Tăng Giáp
-
Các Dạng Toán Về Khảo Sát Hàm Số Bậc Ba, Bậc Bốn Trùng Phương
-
Hướng Dẫn Cách Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc 3 - VOH
-
Phương Pháp Tìm Cực Trị Của Hàm Số Bậc 3 - Vật Lí Phổ Thông