Các Công Thức Logarit, Logarit Nepe (logarit Cơ Số E) Cần Nhớ
Có thể bạn quan tâm
Vậy các công thức logarit, logarit nepe (hay logarit cơ số e) cần nhớ gồm các công thức nào. Bài viết này sẽ tổng hợp lại các công thức logarit, logarit thập phân và logarit nepe cơ bản cần nhớ một cách đầy đủ để các em tham khảo.
» Đừng bỏ lỡ: Cách giải phương trình logarit chứa tham số cực hay
I. LÔGARIT
1. Định nghĩa Logarit
- Cho hai số dương a, b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là lôgarit cơ số α của b, và ký hiệu là logab.
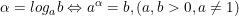
* Ví dụ:
a) 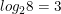 vì
vì 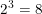
b) 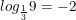 vì
vì 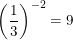
2. Tính chất của lôgarit
- Cho hai số dương a và b, a ≠ 1. Ta có:
•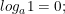 •
•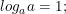
•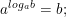 •
•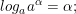
* Ví dụ:
a) 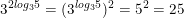
b) 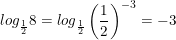
3. Quy tắc tính lôgarit
a) Lôgarit của một tích
• Cho ba số dương a, b1, b2 với a ≠ 1, ta có:
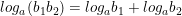
• Lôgarit của một tích bằng tổng các lôgarit
* Ví dụ: Tính log69 + log64
° Lời giải:
- Ta có: log69 + log64 = log6(9.4) = log6(36) = 2.
b) Lôgarit của một thương
• Cho ba số dương a, b1, b2 với a ≠ 1, ta có:
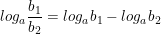
• Lôgarit của một tích bằng hiệu các lôgarit, đặt biệt: 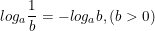
* Ví dụ: Tính log749 + log7343
° Lời giải:
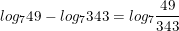
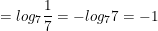
c) Lôgarit của một lũy thừa
• Cho hai số dương a, b; a ≠ 1. Với mọi α ta có:
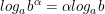
• Lôgarit của một lũy thừa bằng tích của số mũ với logarit của cơ số, đặc biệt:
![small log_{a}sqrt[n]{b}=frac{1}{n}log_ab](https://hayhochoi.vn/uploads/news/wyswyg/2020_06/1592470418vomwober8w.gif)
* Ví dụ: Tính: 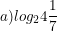
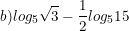
° Lời giải:
a) 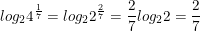
b) 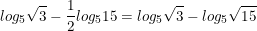
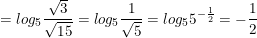
d) Công thức đổi cơ số của Logarit
• Cho ba số dương a, b, c với a ≠ 1, c ≠ 1, ta có: 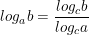
• Đặc biệt: 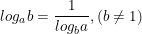 ;
; 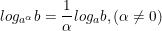
* Ví dụ: Tính 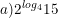
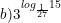
° Lời giải:
a) Ta có: 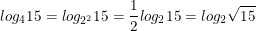
Suy ra 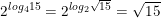
b) Vì 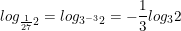
![small =log_{3}2^{-frac{1}{3}}=log_3frac{1}{sqrt[3]{2}}](https://hayhochoi.vn/uploads/news/wyswyg/2020_06/1592470440uhnrhwzl4d.gif)
nên ![small 3^{log_{frac{1}{27}}2}=3^{log_{3}frac{1}{sqrt[3]{2}}}=frac{1}{sqrt[3]{2}}](https://hayhochoi.vn/uploads/news/wyswyg/2020_06/1592470442avdut1c3qp.gif)
II. LÔGARIT thập phân
• Lôgarit thập phân là lôgarit cơ số 10
• log10b thường được viết là logb hoặc lgb.
III. LÔGARIT tự nhiên (Lôgarit nepe, lôgarit cơ số e)
• Dãy số (un) với 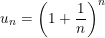 có giới hạn là 1 số vô tỉ và gọi giới hạn đó là e.
có giới hạn là 1 số vô tỉ và gọi giới hạn đó là e.
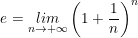
• Logarit tự nhiên là logarit cơ số e.
• logeb được viết là lnb.
→ Khi học các công thức lôgarit các em cần lưu ý điều kiện cơ số của logarit phải dương và khác 1, số hay biểu thức trong lôgarit phải dương.
Công thức mà nhiều em hay nhầm khi giải phương trình logarit sau này đó là logarit của một tích hay logarit của một thương (nguyên nhân do các em không để ý đến điều kiện), ví dụ:
- Với với log3x có nghĩa khi x > 0 nên phép ta có phép biến đổi đúng sau:
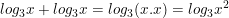
Tuy nhiên nếu biểu thức là log3x2 có nghĩa khi x ≠ 0, phép biến đổi sau sẽ sai:
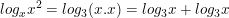
→ Như vậy, các em cần đặc biệt lưu ý về điều kiện lôgarit có nghĩa trong các công thức lôgarit khi biến đổi. Chúc các em học tốt !
Từ khóa » Tính Chất Của Logarit Tự Nhiên
-
Ln (x) - Quy Tắc Logarit Tự Nhiên - RT
-
Lý Thuyết Số E Và Logarit Tự Nhiên Toán 12
-
8+ Các Công Thức Logarit, Logarit Tự Nhiên (logarit Cơ Số E) Cần Nhớ ...
-
Lý Thuyết Số E Và Logarit Tự Nhiên Toán 12
-
Logarit Tự Nhiên - Bảng Tính Trực Tuyến, đồ Thị, Công Thức
-
Logarit Là Gì? Định Nghĩa, Tính Chất Và Các Công Thức Của Logarit
-
9+ Các Công Thức Logarit đầy đủ - .vn
-
Lôgarit Tự Nhiên Là Gì Của 1. Lôgarit Tự Nhiên
-
Logarit Là Gì? Tổng Hợp Các Công Thức Logarit đẩy đủ Nhất
-
Lý Thuyết Khái Niệm Và Tính Chất Của Lôgarit Chi Tiết Và đầy đủ Nhất
-
Logarit (số E Và Logarit Tự Nhiên) | SGK Toán Lớp 12
-
Lý Thuyết Lôgarit | SGK Toán Lớp 12