Các Dạng Bài Tập áp Dụng 7 Hằng đẳng Thức Và Ví Dụ - Toán Lớp 8

 Ví dụ 1: Phân tích đa thức sau thành nhân tử: A = x2 – 4x + 4 – y2

* Lời giải:

- Ta có : A = x2 – 4x + 4 – y2 [để ý x2 – 4x + 4 có dạng hằng đẳng thức]

= (x2 – 4x + 4) – y2  [nhóm hạng tử]

= (x – 2)2 – y2   [xuất hiện đẳng thức số A2 - B2]

= (x – 2 – y )( x – 2 + y)

⇒ A = (x – 2 – y )( x – 2 + y)

 Ví dụ 2: phân tính A thành nhân tử biết: A = x3 – 4x2 + 4x

 = x(x2 – 4x + 4)

= x(x2 – 2.2x + 22)

= x(x – 2)2

 Ví dụ 3: Phân tích B thành nhân tử biết: B = x 2 – 2xy – x + 2y

= (x 2– x) + (2y – 2xy)

= x(x – 1) – 2y(x – 1)

= (x – 1)(x – 2y)

 Ví dụ 4:  Phân tích C thành nhân tử biết: C = x2 – 5x + 6

= x2 – 2x – 3x  + 6

= x(x – 2) – 3(x  – 2)

= (x – 2)(x – 3)

• Dạng 8: Tìm giá trị của x

 Ví dụ: Tìm giá trị củ x biết: x2( x – 3) – 4x + 12 = 0

* Lời giải.

 x2 (x – 3) – 4x + 12 = 0

⇔ x2 (x – 3) – 4(x – 3) = 0

⇔ (x – 3) (x2 – 4) = 0

⇔ (x – 3)(x – 2)(x + 2) = 0

⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0

⇔ x = 3 hoặc x = 2 hoặc x = –2

⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2

• Dạng 9 : Thực hiện phép tính phân thức

 Ví dụ: Tính giá trị của phân thức 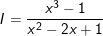  tại x = –1

* Lời giải:

- Ta có :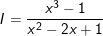

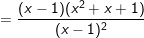
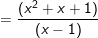
- Khi x = -1 :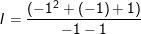

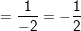
⇒ Kết luận, vậy:  I = 1/2 tại x = -1 .

III. Bài tập áp dụng 7 hằng đẳng thức đáng nhớ

Bài 17 trang 11 SGK toán 8 tập 1: Chứng minh rằng: (10a + 5)2 = 100a(a + 1) + 25

Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.

Áp dụng để tính: 252;     352;     652;     752

* Lời giải Bài 17 trang 11 SGK toán 8 tập 1: 

- Ta có: (10a + 5)2 = (10a)2 + 2.10a.5 + 52 = 100a2 + 100a + 25 = 100a(a + 1) + 25

- Đặt A = a(a + 1). Khi đó ta có:

    

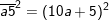
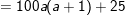
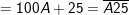
- Do vậy, để tính bình phương của một số tự nhiên có dạng 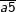 , ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.

* Áp dụng:

 252 = 625 (Vì 2.3 = 6)

 352 = 1225 (Vì 3.4 = 12)

 652 = 4225 (Vì 6.7 = 42)

 752 = 5625 (Vì 7.8 = 56)

Bài 18 trang 11 SGK toán 8 tập 1: Hãy tìm cách giúp bạn An khôi phục lại những hằng đẵng thức bị mực làm nhòe đi một số chỗ:

 a) x2 + 6xy + ... = ( ... + 3y)2

 b) ... - 10xy + 25y2 = ( ... - ...)2

Hãy nêu một đề bài tương tự.

* Lời giải bài 18 trang 11 SGK toán 8 tập 1: 

a) Dễ dàng nhận thấy đây là hằng đẳng thức (A+B)2 với:

 A = x ; 2.AB = 6xy ⇒ B = 3y.

- Vậy ta có hằng đẳng thức: x2 + 2.x.3y + (3y)2 = (x + 3y)2 hay x2 + 6xy + 9y2 = (x + 3y)2

b) Nhận thấy đây là hằng đẳng thức (A-B)2  với:

 B2 = 25y2 = (5y)2 ⇒ B = 5y ; 2.AB = 10xy = 2.x.5y ⇒ A = x.

- Vậy ta có hằng đẳng thức : x2 – 10xy + 25y2 = (x – 5y)2

c) Đề bài tương tự:

 9x2 + 12xy + ... = (... + 4y2)

 ... – 4xy + y2 = ( ... – ...)2

Bài 28 trang 14 SGK toán 8 tập 1: Tính giá trị của biểu thức:

a) x3 + 12x2 + 48x + 64 tại x = 6

b) x3 – 6x2 + 12x – 8 tại x = 22

* Lời giải bài 28 trang 14 SGK toán 8 tập 1:

a) x3 + 12x2 + 48x + 64 = x3 + 3.x2.4 + 3.x.42 + 43 = (x + 4)3

- Tại x = 6, giá trị biểu thức là: (6 + 4)3 = 103 = 1000.

b) x3 – 6x2 + 12x – 8 = x3 – 3.x2.2 + 3.x.22 – 23 = (x – 2)3

- Tại x = 22, giá trị biểu thức là: (22 – 2)3 = 203 = 8000.

Bài 30 trang 16 SGK toán 8 tập 1: Rút gọn các biểu thức sau:

a) (x + 3)(x2 – 3x + 9) – (54 + x3)

b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)

* Lời giải bài 30 trang 16 SGK toán 8 tập 1:

a) (x + 3)(x2 – 3x + 9) – (54 + x3)

 [có dạng hằng đẳng thức A3+B3]

 = (x3 + 33) – (54 + x3)

 = x3 + 27 – 54 – x3

 = –27

b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)

 [có dạng hằng đẳng thức A3 + B3 và A3 - B3]

= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]

= [(2x)3 + y3] – [(2x)3 – y3]

= (2x)3 + y3 – (2x)3 + y3

= 2y3

Bài 31 trang 16 SGK toán 8 tập 1: Chứng minh rằng:

a) a3 + b3 = (a + b)3 – 3ab(a + b)

b) a3 – b3 = (a – b)3 + 3ab(a – b)

Áp dụng: Tính a3 + b3, biết a.b = 6 và a + b = -5

* Lời giải bài 31 trang 16 SGK toán 8 tập 1:

a) Biến đổi vế phải ta được:

VP = (a + b)3 – 3ab(a + b)

 = a3 + 3a2b + 3ab2 + b3 – 3a2b – 3ab2

 = a3 + b3 = VT

- Kết luận, vậy: a3 + b3 = (a + b)3 – 3ab(a + b)

b) Biến đổi vế phải ta được:

VP = (a – b)3 + 3ab(a – b)

 = a3 – 3a2b + 3ab2 – b3 + 3a2b – 3ab2

 = a3 – b3 = VT

- Kết luận, vậy: a3 – b3 = (a – b)3 + 3ab(a – b)

* Áp dụng: Với ab = 6, a + b = –5, ta có:  a3 + b3 = (a + b)3 – 3ab(a + b)

 = (–5)3 – 3.6.(–5) = –53 + 3.6.5 = –125 + 90 = –35

Bài 34 trang 17 SGK toán 8 tập 1: Rút gọn các biểu thức sau:

a) (a + b)2 – (a – b)2

b) (a + b)3 – (a – b)3 – 2b3

c) (x + y + z)2 – 2(x + y + z)(x + y) + (x + y)2

* Lời giải bài 34 trang 17 SGK toán 8 tập 1:

a) (a + b)2 – (a – b)2

♦ Cách 1: [Áp dụng HĐT A2 - B2 với A = a + b; B = a – b]

= [(a + b) – (a – b)].[(a + b) + (a – b)]

= 2b.2a = 4ab

♦ Cách 2: [Áp dụng (A+B)2 và (A-B)2

= a2 + 2ab + b2 - (a2 - 2ab + b2)

= a2 + 2ab + b2 - a2 + 2ab - b2

=  4ab

b) (a + b)3 – (a – b)3 – 2b3

= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3) – 2b3 

= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3 – 2b3

= (a3 – a3) + (3a2b + 3a2b) + (3ab2 – 3ab2) + (b3 + b3 – 2b3)

= 6a2b

c) (x + y + z)2 – 2.(x + y + z).(x + y) + (x + y)2

 [áp dụng HĐT (A-B)2 với A = x + y + z ; B = x + y)]

= [(x + y + z) – (x + y)]2 = z2.

IV. Một số bài tập vận dụng 7 hàng đẳng thức luyện tập

Bài tập 1: Viết các biểu thức sau dưới dạng bình phương của 1 tổng hay 1 hiệu:

a)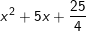 

b) 16x2 - 8x + 1

c) 4x2 +12xy +9y2

d) (x+3)(x+4)(x+5)(x+6)+1

Đ/S: a) (x+5/2)2 ; b) (4x-1)2 ; c) (2x+3y)2 ; d) (x2+9x+19)2

Bài tập 2: Viết các biểu thức sau dưới dạng lập phương của 1 tổng hay 1 hiệu:

a) x3 + 3x2 + 3x +1

b) 27x3 - 9x2 + x - 1/27

c) 8x6 + 12x4y + 6x2y2 + y3

d) (x+y)3(x-y)3

Đ/S: a) (x+1)3 ; b) 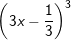 ; c) (2x2 + y)3 ; d) (x2-y2)3

Bài tập 3: Rút gọn biểu thức

a) A = (2x+3)2 -2(2x+3)(2x+5) + (2x+5)2

b) B = (x2+x+1)(x2-x+1)(x2-1)

c) C = (x+y-z)2 + (x-y+z)2 - 2(y-z)2

d) D = (x+y+z)2 + (x-y-z)2 - 2(y-z)2

Đ/S: a) A=4 ; b) B=x6-1 ; c) C=2x2 ; d) D=2(x2+4yz)

Bài tập 4: Điền đơn thức thích hợp vào dấu *

a) 8x3 + *  + * + 27y3 = (* + *)3

b) 8x3 + 12x2y + * + * = (* + *)3

c) x3 - * + * - * = (* - 2y)3

Đ/S: a) (2x+3y)3 ; b) (2x+y)3 ; c) (x-2y)3

Bài tập 5: chứng minh rằng với mọi giá trị của x ta có:

a) -x2 + 6x - 10 < 0

b) x4 + 3x2 +3 > 0

Bài tập 6: Cho a - b = m; a.b = n. Tính theo m, n giá trị biểu thức sau:

 1) A= (a + b)2

 2) B= a2 + b2

 3) C= a3 - b3

Đ/S: a) A = m2+ 4n ;  b) B = m2 - 2n ; c) C = m(m2 + 3n)

Bài tập 7: Tính giá trị của biểu thức bằng cách vận dụng hằng đẳng thức

a) A = x3 + 3x2 + 3x + 6 với x = 29

b) B =  x3 - 3x2 + 3x - 1 với x = 21

Đ/S: A = 27005 ; B = 8000