Các Dạng Hệ Phương Trình đặc Biệt - Chuyên đề Môn Toán Lớp 10

Các dạng hệ phương trình đặc biệt Chuyên đề môn Toán lớp 10 Bài trước Tải về Bài sau Lớp: Lớp 10 Môn: Toán Dạng tài liệu: Chuyên đề Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Chuyên đề Toán học lớp 10: Các dạng hệ phương trình đặc biệt được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

Chuyên đề: Các dạng hệ phương trình đặc biệt

• I. Lý thuyết & Phương pháp giải
• II. Ví dụ minh họa

I. Lý thuyết & Phương pháp giải

DẠNG TOÁN 1: HỆ GỒM MỘT PHƯƠNG TRÌNH BẬC NHẤT VÀ MỘT BẬC HAI

Phương pháp giải

Sử dụng phương pháp thế

- Từ phương trình bậc nhất rút một ẩn theo ẩn kia.

- Thế vào phương trình bậc hai để đưa về phương trình bậc hai một ẩn.

- Số nghiệm của hệ tùy theo số nghiệm của phương trình bậc hai này.

DẠNG TOÁN 2: HỆ PHƯƠNG TRÌNH ĐỐI XỨNG

1. Phương pháp giải

a. Hệ đối xứng loại 1

Hệ phương trình đối xứng loại 1 là hệ phương trình có dạng:

(I)   \(\left\{ \begin{gathered} f\left( {x;y} \right) = 0 \hfill \\ g\left( {x;y} \right) = 0 \hfill \\ \end{gathered} \right.\) với  \(\left\{ \begin{gathered} f\left( {x;y} \right) = f\left( {y;x} \right) \hfill \\ g\left( {x;y} \right) = g\left( {y;x} \right) \hfill \\ \end{gathered} \right.\)

(Có nghĩa là khi ta hoán vị giữa x và y thì f(x, y) và g(x, y) không thay đổi).

Cách giải

- Đặt S = x + y, P = xy

- Đưa hệ phương trình (I) về hệ (I') với các ẩn là S và P.

- Giải hệ (I') ta tìm được S và P

- Tìm nghiệm (x; y) bằng cách giải phương trình: X2 - SX + P = 0

b. Hệ đối xứng loại 2

Hệ phương trình đối xứng loại 2 là hệ phương trình có dạng:

\(\left( {II} \right):\left\{ \begin{gathered} f\left( {x;y} \right) = 0{\text{ }}\left( 1 \right) \hfill \\ g\left( {x;y} \right) = 0{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.\)

(Có nghĩa là khi hoán vị giữa x và y thì (1) biến thành (2) và ngược lại)

- Trừ (1) và (2) vế theo vế ta được: (II) ⇔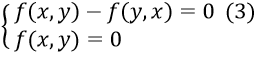

- Biến đổi (3) về phương trình tích: (3) ⇔ (x-y).g(x,y) = 0 ⇔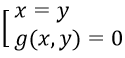

- Như vậy (II) ⇔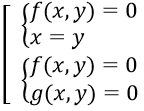

- Giải các hệ phương trình trên ta tìm được nghiệm của hệ (II)

c. Chú ý: Hệ phương trình đối xứng loại 1, 2 nếu có nghiệm là (x0; y0) thì (y0; x0) cũng là một nghiệm của nó

DẠNG TOÁN 3: HỆ PHƯƠNG TRÌNH ĐẲNG CẤP BẬC HAI

1. Phương pháp giải

Hệ phương trình đẳng cấp bậc hai là hệ phương trình có dạng:

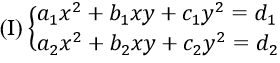
- Giải hệ khi x = 0 (hoặc y = 0)

- Khi x ≠ 0, đặt y = tx. Thế vào hệ (I) ta được hệ theo k và x. Khử x ta tìm được phương trình bậc hai theo k. Giải phương trình này ta tìm được k, từ đó tìm được (x; y)

II. Ví dụ minh họa

Bài 1: Giải hệ phương trình

a. \(\left\{ \begin{gathered} x + y + xy = 5 \hfill \\ {x^2} + {y^2} = 5 \hfill \\ \end{gathered} \right.\)                  b. \(\left\{ \begin{gathered} x\left( {x + y + 1} \right) - 3 = 0 \hfill \\ {\left( {x + y} \right)^2} - \frac{5}{{{x^2} + 1}} = 0 \hfill \\ \end{gathered} \right.\)

Hướng dẫn:

a. Đặt S = x + y, P = xy (S2 - 4P ≥ 0)

Ta có: \(\left\{ \begin{gathered} S + P = 5 \hfill \\ {S^2} - 2P = 5 \hfill \\ \end{gathered} \right.\)

⇒S2 - 2(5-S) = 5 ⇒ S2 + 2S - 15 = 0

⇒ S = -5; S = 3

S = -5⇒ P = 10 (loại)

S = 3⇒ P = 2 (nhận)

Khi đó : x, y là nghiệm của phương trình X2 - 3X + 2 = 0

⇔ X = 1; X = 2

Vậy hệ có nghiệm (2; 1), (1; 2)

b. ĐKXĐ: x ≠ 0

Hệ phương trình tương đương với

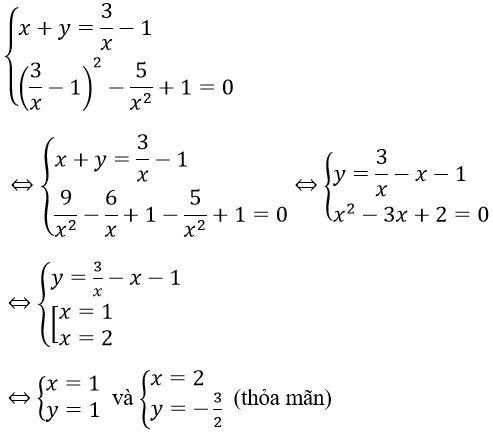
Vậy hệ phương trình có nghiệm (x; y) là (1; 1) và (2; -3/2)

Bài 2: Giải hệ phương trình

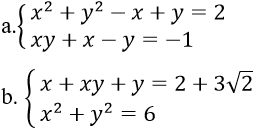
Hướng dẫn:

a. Hệ phương trình tương đương

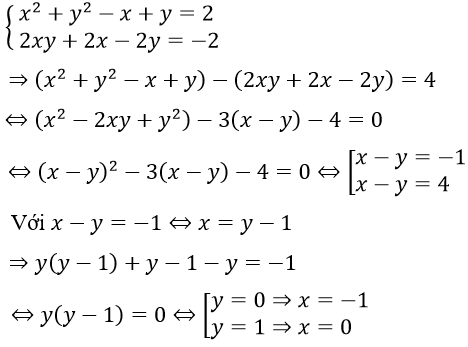
Với x-y = 4 ⇒ x = y + 4 ⇒ y(y+4) + y + 4 - y = -1

⇔ y2 + 4y + 5 = 0 (vn)

Vậy nghiệm của hệ phương trình là (x; y) = {(0; 1), (-1; 0)}

b. Đặt S = x+y; P = xy, ta có hệ:

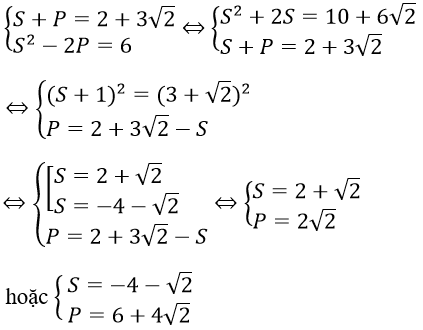
- Với S = 2 + √2; P = 2√2 ta có x, y là nghiệm phương trình:

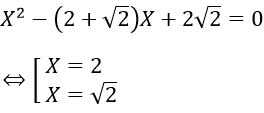
Với S = -4-√2; P = 6 + 4√2 ta có x, y là nghiệm phương trình:

X2 + (4+√2)X + 6 + 4√2 = 0 (vô nghiệm)

Vậy hệ có nghiệm (x; y) là (2; √2) và (√2; 2)

Bài 3: Giải hệ phương trình:

a. \(\left\{ \begin{gathered} {x^2} + x = 3y \hfill \\ {y^2} + y = 3x \hfill \\ \end{gathered} \right.\)                            b. \(\left\{ \begin{gathered} {y^2} = {x^3} - 3{x^2} + 2x \hfill \\ {x^2} = {y^3} - 3{y^2} + 2y \hfill \\ \end{gathered} \right.\)

Hướng dẫn:

a. Hệ phương trình tương đương

\(\left( {{x^2} + x} \right) - \left( {{y^2} + y} \right) = 3y - 3x\)

\(\Leftrightarrow \left( {x - y} \right)\left( {x + y + 4} \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = y \hfill \\ x = y - 4 \hfill \\ \end{gathered} \right.\)

Với x = y \(\Rightarrow {x^2} + x = 3x \Leftrightarrow {x^2} - 2x = 0\)

\(\Leftrightarrow \left[ \begin{gathered} x = 0 \Rightarrow y = 0 \hfill \\ x = 2 \Rightarrow y = 2 \hfill \\ \end{gathered} \right.\)

Với x = y - 5 \(\Rightarrow {y^2} + y = 3\left( { - y - 4} \right)\)

\(\Leftrightarrow {y^2} + 4y + 12 = 0\left( {VN} \right)\)

Vậy tập nghiệm của hệ phương trình là: (x; y) = {(0;0), (2;2)}

b. Trừ vế với vế của phương trình đầu và phương trình thứ hai ta được:

(y2 - x2 = x3 - y3 - 3(x2 - y2) + 2(x-y)

⇔ (x-y)(x2 + xy + y2 - 2x - 2y + 2) = 0

⇔ 1/2(x-y)[x2 + y2 + (x + y - 2)2] = 0 ⇔ x = y)

(vì x2 + y2 + (x+y-2)2 > 0)

Thay x = y vào phương trình đầu ta được:

x3 - 4x2 + 2x = 0 ⇔ x(x2 - 4x + 2) = 0

\(\Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ {x^2} - 4x + 2 = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = 2 \pm \sqrt 2 \hfill \\ \end{gathered} \right.\)

Vậy hệ phương trình có ba nghiệm: (0; 0); (2+√2; 2+√2) và (2-√2; 2-√2)

Bài 4: Giải hệ phương trình:

a. \(\left\{ \begin{gathered} {x^3} - 3x = {y^3} - 3y \hfill \\ {x^6} + {y^6} = 27 \hfill \\ \end{gathered} \right.\)                         b. \(\left\{ \begin{gathered} {x^2} + {y^2} - x + y = 2 \hfill \\ xy + x - y = - 1 \hfill \\ \end{gathered} \right.\)

Hướng dẫn:

a. Ta có : x3 - 3x = y3 - 3y ⇔ (x-y)(x2 + xy + y2) - 3(x-y) = 0

⇔ (x-y)(x2 + xy + y2 - 3) = 0

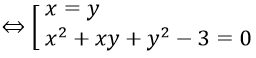
Khi x = y thì hệ có nghiệm

Khi x2 + xy + y2 - 3 = 0 ⇔ x2 + y2 = 3 - xy, ta có x6 + y6 = 27

⇔ (x2 + y2)(x4 - x2y2 + y4) = 27

⇒ (3-xy)[(3-xy)2 - 3x2y2] = 27 ⇔ 3(xy)3 + 27xy = 0

\(\left[ \begin{gathered} xy = 0 \hfill \\ {\left( {xy} \right)^2} = - 9 \hfill \\ \end{gathered} \right.\) (Vô lý)

Vậy hệ phương trình đã cho có 2 nghiệm

\(\left( {x;y} \right) = \left( {\sqrt[6]{{\frac{{27}}{2}}};\sqrt[6]{{\frac{{27}}{2}}}} \right) = \left( { - \sqrt[6]{{\frac{{27}}{2}}}; - \sqrt[6]{{\frac{{27}}{2}}}} \right)\)

b. Hệ phương trình tương đương

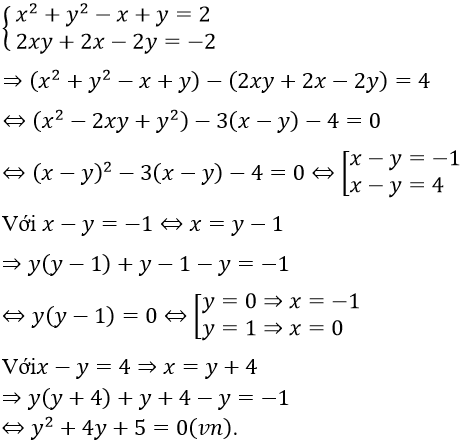
Bài 5: Xác định m để hệ phương trình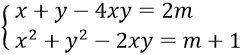có nghiệm

Hướng dẫn:

Hệ phương trình tương đương

(x2 + y2 - 2xy) - (x + y - 4xy) = m + 1 - 2m ⇔ (x+y)2 - (x+y) + m - 1 = 0

Để hệ phương trình có nghiệm Δ ≥ 0 ⇔ 1 - 4(m-1) ≥ 0 ⇔ 5 - 4m ≥ 0

⇔ m ≤ 5/4

Từ phương trình thứ 2 ta có(x-y)2 = m + 1 ⇒ m + 1 ≥ 0 ⇔ m ≥ -1

Do đó -1 ≤ m ≤ 5/4.

III. Một số phương pháp giải hệ phương trình nâng cao 

1. Áp dụng bất đẳng thức giải hệ phương trình

Ví dụ. Giải các hệ phương trình: \(\left\{ \begin{matrix} x + y + z = 1 \\ x^{4} + y^{4} + z^{4} = xyz \\ \end{matrix} \right.\)

Hướng dẫn giải

Nhận xét: Từ BĐT \((a - b)^{2} + (b - c)^{2} + (c - a)^{2} \geq 0\)

Ta suy ra: \(a^{2} + b^{2} + c^{2} \geq ab + bc + ca(*)\)

Áp dụng liên tiếp BĐT (*) ta được

\(x^{4} + y^{4} + z^{4} \geq x^{2}y^{2} + y^{2}z^{2} + z^{2}x^{2} \geq xyz(x + y + z)\)

\(\Leftrightarrow x^{4} + y^{4} + z^{4} \geq xyz\)

Đẳng thức xẩy ra khi: \(x = y = z = \frac{1}{3}\)

Vậy hệ đã cho có nghiệm là: \((x;y;z) = \left( \frac{1}{3};\frac{1}{3};\frac{1}{3} \right)\)

Ví dụ: Giải hệ phương trình: \(\left\{ \begin{matrix} \sqrt{x} + \sqrt[4]{32 - x} = y^{2} - 3 \\ \sqrt[4]{x} + \sqrt{32 - x} = 24 - 6y \\ \end{matrix} \right.\)

Hướng dẫn giải

Điều kiện xác định: \(0 \leq x \leq 32\)

Hệ đã cho tương đương với

\(\left\{ \begin{matrix} (\sqrt{x} + \sqrt{32 - x}) + (\sqrt[4]{x} + \sqrt[4]{32 - x}) = y^{2} - 6y + 21 \\ \sqrt{x} + \sqrt[4]{32 - x} = y^{2} - 3 \\ \end{matrix} \right.\)

Theo bất đẳng thức Bunhiacốpxki ta có

\((\sqrt{x} + \sqrt{32 - x})^{2} \leq (1^{2} + 1^{2})(x + 32 - x) = 64\)

\(\Rightarrow \sqrt{x} + \sqrt{32 - x} \leq 8\)

\(\left( \sqrt[4]{x} + \sqrt[4]{32 - x} \right)^{4} \leq \left\lbrack 2(\sqrt{x} + \sqrt{32 - x}) \right\rbrack^{2} \leq 256\)

\(\Rightarrow \sqrt[4]{x} + \sqrt[4]{32 - x} \leq 4\)

Suy ra \((\sqrt{x} + \sqrt{32 - x}) + (\sqrt[4]{x} + \sqrt[4]{32 - x}) \leq 12\)

Mặt khác \(y^{2} - 6y + 21 = (y - 3)^{2} + 12 \geq 12\)

Đẳng thức xẩy ra khi x = 16 và y = 3 (thỏa mãn)

Vậy hệ đã có nghiệm là (x; y) = (16; 3)

2. Phương pháp đặt ẩn phụ

Ví dụ:  Giải các hệ phương trình: \(\left\{ \begin{matrix} x^{2} + x = 5 + y^{2} + y \\ x^{3} + y^{3} = x^{2}y + xy^{2} + 6 \\ \end{matrix} \right.\).

Hướng dẫn giải

Đặt: x - y = a; x + y = b

Hệ phương trình đã cho trở thành \(\left\{ \begin{matrix} ab + a = 5(1) \\ a^{2}b = 6(2) \\ \end{matrix} \right.\)

Từ phương trình (2) ta suy ra \(a \neq 0\)

Do đó: \(b = \frac{6}{a^{2}}\)

Thế vào (1) ta được: \(\frac{6}{a} + a = 5\)

\(\Leftrightarrow a^{2} - 5a + 6 = 0\) (Vì \(a \neq 0\))

\(\Leftrightarrow (a - 2)(a - 3) = 0\) \(\Leftrightarrow \left\{ \begin{matrix} a = 2 \\ a = 3 \\ \end{matrix} \right.\)

+) \(a = 2 \Rightarrow b = \frac{3}{2}\) hay \(\left\{ \begin{matrix} x + y = \frac{3}{2} \\ x - y = 2 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{7}{4} \\ y = \frac{- 1}{4} \\ \end{matrix} \right.\)

+) \(a = 3 \Rightarrow b = \frac{2}{3}\) hay \(\left\{ \begin{matrix} x + y = \frac{2}{3} \\ x - y = 3 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{11}{6} \\ y = \frac{- 7}{6} \\ \end{matrix} \right.\)

Tóm lại hệ phương trình đã cho có nghiệm là:

(x; y) = \(\left( \frac{7}{4};\frac{- 1}{4} \right);\left( \frac{11}{6};\frac{- 7}{6} \right)\)

Ví dụ: Giải hệ phương trình: \(\left\{ \begin{matrix} x^{3} + x^{3}y^{3} + y^{3} = 17 \\ x + xy + y = 5 \\ \end{matrix} \right.\)

Hướng dẫn giải

Đặt x + y = a; x.y = b

Hệ đã cho trở thành

\(\left\{ \begin{matrix} a^{3} + b^{3} - 3ab = 17 \\ a + b = 5 \\ \end{matrix} \right.\) \(\Leftrightarrow \left\{ \begin{matrix} a = 5 - b \\ b^{2} - 5b + 6 = 0 \\ \end{matrix} \right.\) \(\Leftrightarrow \left\{ \begin{matrix} a = 5 - b \\ (b - 2)(b - 3) = 0 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} a = 3 \\ b = 2 \\ \end{matrix} \right.\) Hoặc \(\left\{ \begin{matrix} a = 2 \\ b = 3 \\ \end{matrix} \right.\)

Với \(\left\{ \begin{matrix} a = 3 \\ b = 2 \\ \end{matrix} \right.\) ta có hệ phương trình \(\left\{ \begin{matrix} x + y = 3 \\ xy = 2 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} x = 3 - y \\ y^{2} - 3y + 2 = 0 \\ \end{matrix} \right.\) \(\Leftrightarrow \left\{ \begin{matrix} x = 3 - y \\ (y - 1)(y - 2) = 0 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} x = 2 \\ y = 1 \\ \end{matrix} \right.\) Hoặc \(\left\{ \begin{matrix} x = 1 \\ y = 2 \\ \end{matrix} \right.\)

Với \(\left\{ \begin{matrix} a = 2 \\ b = 3 \\ \end{matrix} \right.\)  ta có hệ phương trình \(\left\{ \begin{matrix} x + y = 2 \\ xy = 3 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} x = 2 - y \\ y^{2} - 2y + 3 = 0 \\ \end{matrix} \right.\) (Vô nghiệm)

Hệ này vô nghiệm

Vậy nghiệm của hệ đã cho là:(x;y) = (1;2); (2;1)

Ví dụ: Tìm nghiệm của hệ phương trình \(\left\{ \begin{matrix} (x + y)^{4} = 6x^{2}y^{2} - 215 \\ xy(x^{2} + y^{2}) = - 78 \\ \end{matrix} \right.\)

Hướng dẫn giải

Hệ đã cho tương đương với

\(\left\{ \begin{matrix} x^{4} + 4x^{3}y + 4xy^{3} + y^{4} = - 215 \\ x^{3}y + xy^{3} = - 78 \\ \end{matrix} \right.\) \(\Leftrightarrow \left\{ \begin{matrix} 78x^{4} + 312x^{3}y + 312xy^{3} + 78y^{4} = - 16770 \\ 215x^{3}y + 215xy^{3} = - 16770 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} 78x^{4} + 97x^{3}y + 97xy^{3} + 78y^{4} = 0(1) \\ x^{3}y + xy^{3} = - 78 \\ \end{matrix} \right.\)

Đặt \(t = \frac{x}{y}\) PT (1) trở thành \(78t^{4} + 97t^{3} + 97t + 78 = 0\)

\(\Leftrightarrow (3t + 2)(2t + 3)(13t^{2} - 12t + 13) = 0\) \(\Leftrightarrow \left\lbrack \begin{matrix} t = \frac{- 2}{3} \\ t = \frac{- 3}{2} \\ \end{matrix} \right.\)

+)\(t = \frac{- 2}{3} \Rightarrow x = \frac{- 2}{3}y\)

Thế vào (2) ta được \(\frac{26}{27}y^{4} = 78\)

\(\Leftrightarrow y^{4} = 81\)

\(\Leftrightarrow y = 3\) Hoặc \(y = - 3\)

Suy ra: \(\left\{ \begin{matrix} x = - 2 \\ y = 3 \\ \end{matrix} \right.\) Hoặc \(\left\{ \begin{matrix} x = 2 \\ y = - 3 \\ \end{matrix} \right.\)

+)\(t = \frac{- 3}{2} \Rightarrow x = \frac{- 3}{2}y\)

Thế vào (2) ta được \(\frac{39}{8}y^{4} = 78\)

\(\Leftrightarrow y^{4} = 16\)

\(\Leftrightarrow y = 2\) Hoặc \(y = - 2\)

Suy ra: \(\left\{ \begin{matrix} x = - 3 \\ y = 2 \\ \end{matrix} \right.\) Hoặc \(\left\{ \begin{matrix} x = 3 \\ y = - 2 \\ \end{matrix} \right.\)

Tóm lại hệ đã cho có nghiệm là:

(x;y) = (-2;3); (2;-3); (-3;2) ; (3;-2)

--------------------------------------------------------------------

Với nội dung bài Các dạng phương trình đặc biệt trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững khái niệm, phương pháp giải các dạng phương trình đặc biệt...

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Các dạng hệ phương trình đặc biệt. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc