Lý Thuyết Về Phương Trình Và Hệ Phương Trình Bậc Nhất Nhiều ẩn
Có thể bạn quan tâm
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn (\(x\) và \(y\)) có dạng: \(ax + by =c\) (1) trong đó \(a, b, c\), là các số đã cho, với \(ab ≠ 0\).
Nếu có cặp số c sao cho \(a{x_0} + b{y_0} = c\) thì \(({x_0};{y_0})\) được gọi là một nghiệm của phương trình (1).
2. Giải và biện luận phương trình \(ax + by = c\) (\(ab ≠ 0\))
+ Nếu \(a ≠ 0, b ≠ 0\) phương trình có vô số nghiệm, mỗi cặp số \((x, y)\), trong đó
\(\left\{\begin{matrix} x\in\mathbb R & \\ y=\dfrac{c-ax}{b}& \end{matrix}\right.\) hoặc \(\left\{\begin{matrix} y\in\mathbb R & \\ x=\dfrac{c-by}{a}& \end{matrix}\right.\) đều là nghiệm của phương trình.
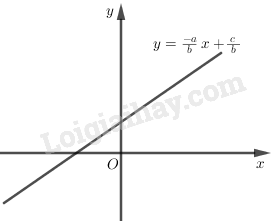
Tập nghiệm của phương trình biểu diễn trên mặt phẳng tọa độ là đồ thị của hàm số \(y = \dfrac{-a}{b}x+\dfrac{c}{b}\). Ta cũng gọi đồ thị đó là đường thẳng \(ax + by = c\).
+ Nếu \(a = 0, b ≠ 0\) mỗi cặp số \((x; y)\) trong đó
\(\left\{ \matrix{ x \text { là số tùy ý }\hfill \cr y = {c \over b} \hfill \cr} \right.\)
là một nghiệm của phương trình.
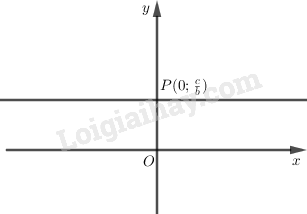
Tập nghiệm của phương trình được biểu diễn trên mặt phẳng tọa độ bằng đường thẳng song song với trục hoành cắt trục tung tại điểm \(P(0; \dfrac{c}{b})\).
+ Nếu \(a ≠ 0, b = 0\), tập nghiệm của phương trình là các cặp số \((x, y)\) trong đó \(\left\{\begin{matrix} x=\dfrac{c}{a} & \\ y& \end{matrix}\right.\) là số tùy ý.
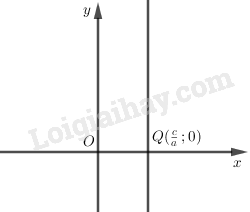
Đường thẳng \(x = \dfrac{c}{a}\) song song với trục tung và cắt trục hoành tại điểm \(Q(\dfrac{c}{a}; 0)\) biểu diễn tập nghiệm của phương trình.
3. Hệ hai phương trình bậc nhất hai ẩn
là hệ phương trình có dạng: (I) \(\left\{\begin{matrix} a_{1}x+b_{1}y=c_{1} (1)& \\ a_{2}x+b_{2}y=c_{2}(2)& \end{matrix}\right.\)
trong đó (1) và (2) là các phương trình bậc nhất hai ẩn.
Một cặp số \(({x_0};{y_0})\) đồng thời là nghiệm của (1) và của (2) gọi là một nghiệm của hệ (I).
Có thể giải hệ hai phương trình bậc nhất hai ẩn bằng phương pháp thế hay phương pháp cộng đại số.
4. Hệ ba phương trình bậc nhất ba ẩn
Để giải ta dùng phương pháp cộng đặc số để đưa về hệ phương trình tương đương có dạng tam giác hoặc dùng phương pháp thế để đưa về việc giải một hệ phương trình bậc nhất hai ẩn.
Loigiaihay.com
Từ khóa » Hệ Phương Trình Lớp 10
-
Cách Giải Các Dạng Hệ Phương Trình đặc Biệt Cực Hay, Chi Tiết
-
Lý Thuyết, Các Dạng Toán Và Bài Tập Phương Trình Và Hệ Phương Trình
-
Toán 10 Bài 3: Phương Trình Và Hệ Phương Trình Bậc Nhất Nhiều ẩn
-
Các Dạng Hệ Phương Trình đặc Biệt - Chuyên đề Môn Toán Lớp 10
-
Các Dạng Toán Giải Phương Trình, Hệ Phương Trình Và Bài Tập Có Lời Giải
-
Giải Hệ Phương Trình Lớp 10 - Phương Pháp Và Bài Tập Có Giải
-
Bài Tập Giải Phương Trình, Hệ Phương Trình Môn Toán Lớp 10
-
Bài Tập Đại Số Lớp 10 - Chương III: Phương Trình Và Hệ Phương Trình
-
Ôn Tập Môn Toán Lớp 10 - Hệ Phương Trình Có Chứa Tham Số
-
Cách Giải Và Biện Luận Hệ Phương Trình Bậc Nhất Cực Hay - Toán Lớp ...
-
Tổng Hợp Lý Thuyết Chương 3: Phương Trình, Hệ ... - Haylamdo
-
Kiến Thức Cơ Bản Đại Số Lớp 10: Phương Trình Và Hệ Phương Trình
-
Phương Pháp Giải Hệ Phương Trình đối Xứng Lớp 10