Các Hệ Thức Độc Lập Với Thời Gian

Ví dụ minh họa:

Hướng dẫn:

 

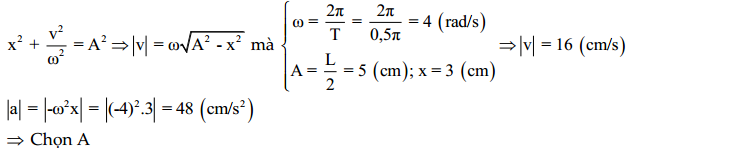
Hướng dẫn:

 

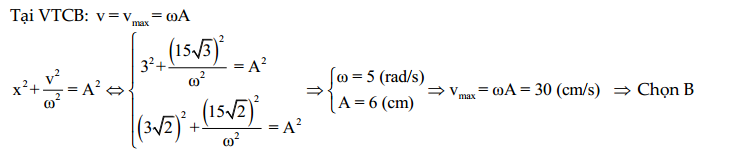
Hướng dẫn:

 

\[\frac{{{v}^{2}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{2}}}+\frac{{{a}^{2}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{4}}}={{A}^{2}}\xrightarrow{\text{ }\!\!\omega\!\!\text{ }=\sqrt{\frac{k}{m}}=\sqrt{\frac{20}{0,2}}=10}A=\sqrt{\frac{0,{{2}^{2}}}{1{{0}^{2}}}+\frac{{{\left( 2\sqrt{3} \right)}^{2}}}{1{{0}^{4}}}}=0,04 (m)=4 \left( cm \right)\] $\Rightarrow $ Chọn B

 

Hướng dẫn:

 

 

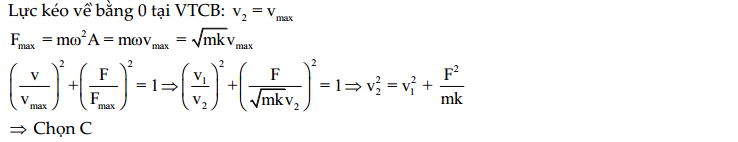
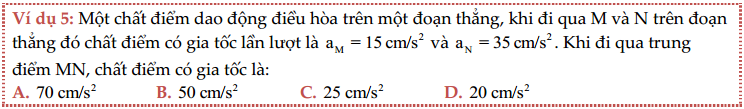
Hướng dẫn:

 

 

$\text{x = }\frac{{{\text{x}}_{\text{M}}}\text{ + }{{\text{x}}_{\text{N}}}}{\text{2}}\xrightarrow{\text{a = -}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}\text{x}}\text{ a = }\frac{{{\text{a}}_{\text{M}}}\text{ + }{{\text{a}}_{\text{N}}}}{\text{2}}\text{ = }\frac{\text{15 + 35}}{\text{2}}\text{ = 25 (cm/}{{\text{s}}^{\text{2}}}\text{)}$ $\Rightarrow $ Chọn C

 

Hướng dẫn:

 

 

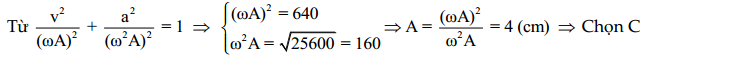
Hướng dẫn:

\[{{\text{x}}^{\text{2}}}\text{ + }\frac{{{\text{v}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ = }{{\text{A}}^{\text{2}}}\Rightarrow \left| \text{x} \right|\text{ = }\sqrt{{{\text{A}}^{\text{2}}}\text{ - }\frac{{{\text{v}}^{\text{2}}}}{{{\text{(2 }\!\!\pi\!\!\text{ f)}}^{\text{2}}}}}\text{ }\Rightarrow \frac{\left| {{\text{x}}_{\text{2}}} \right|}{\left| {{\text{x}}_{\text{1}}} \right|}\text{ = }\frac{\sqrt{{{\text{A}}^{\text{2}}}\text{ - }\frac{{{\text{(4,8 }\!\!\pi\!\!\text{ fA)}}^{\text{2}}}}{\text{(2 }\!\!\pi\!\!\text{ }\text{.4f)}}}}{\sqrt{{{\text{A}}^{\text{2}}}\text{ - }\frac{{{\text{(4,8 }\!\!\pi\!\!\text{ fA)}}^{\text{2}}}}{\text{(2 }\!\!\pi\!\!\text{ }\text{.3f)}}}}\text{ = }\frac{\sqrt{{{\text{A}}^{\text{2}}}\text{ - (0,6A}{{\text{)}}^{\text{2}}}}}{\sqrt{{{\text{A}}^{\text{2}}}\text{ - (0,8A}{{\text{)}}^{\text{2}}}}}\text{ = }\frac{\text{4}}{\text{3}}\text{ = }\frac{\text{12}}{\text{9}}\]

 

$\Rightarrow $ Chọn B

 

Hướng dẫn:

 

 

\[{{m}_{1}}\omega _{1}^{2}{{A}_{1}}={{m}_{2}}\omega _{2}^{2}{{A}_{2}}\to \frac{{{m}_{2}}}{{{m}_{1}}}=\frac{\omega _{1}^{2}{{A}_{1}}}{\omega _{2}^{2}{{A}_{2}}}={{\left( \frac{{{\omega }_{1}}{{A}_{1}}}{{{\omega }_{2}}{{A}_{2}}} \right)}^{2}}.\frac{{{A}_{2}}}{{{A}_{1}}}\xrightarrow[{{\omega }_{1}}{{A}_{1}}=3{{\omega }_{2}}{{A}_{2}}]{3{{A}_{1}}={{A}_{2}}}\frac{{{m}_{2}}}{{{m}_{1}}}={{3}^{2}}.3=27\] $\Rightarrow $ Chọn D.

 

Hướng dẫn:

 

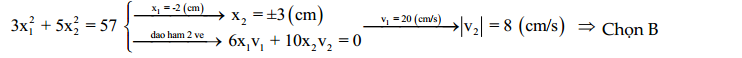
Bài tập tự luyện:

Câu 1: Một vật dao động điều hòa với biên độ A, tần số góc $\text{ }\!\!\omega\!\!\text{ }$. Khi vật cách vị trí cân bằng $\text{0,5A}$ thì tốc độ của vật là:

A. $\text{ }\!\!\omega\!\!\text{ A}$              B. $\frac{\text{ }\!\!\omega\!\!\text{ A}}{\text{2}}$                         C. $\frac{\text{ }\!\!\omega\!\!\text{ A}\sqrt{\text{2}}}{\text{2}}$               D. $\frac{\text{ }\!\!\omega\!\!\text{ A}\sqrt{\text{3}}}{\text{2}}$

Câu 2: Một vật dao động điều hòa với biên độ A, vận tốc cực đại là ${{\text{v}}_{\text{max}}}$. Vật có tốc độ $\text{0,6}{{\text{v}}_{\text{max}}}$ khi li độ của vật có độ lớn là:

 

A. $\text{0,4A}$                 B. $\text{0,8A}$                 C. $\text{0,6A}$                 D. $\text{0,5A}$

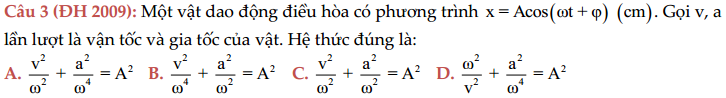
Câu 4: Một vật dao động điều hòa với biên độ A, tần số góc $\omega $. Tại một thời điểm, li độ x, vận tốc v và gia tốc a của vật có hệ thức đúng là:

A. \[\frac{{{\text{v}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ + }\frac{{{\text{a}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ = }{{\text{A}}^{\text{2}}}\]            B. \[\frac{{{\text{x}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}}\text{ + }\frac{{{\text{a}}^{\text{2}}}}{{{\text{ }\!\!\omega\!\!\text{ }}^{\text{4}}}}\text{ = }{{\text{A}}^{\text{2}}}\]       C. $\text{a = - }\!\!\omega\!\!\text{ x}$                   D. $\text{a = -}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}\text{x}$

Câu 5 (CĐ-2012): Một vật dao động điều hòa với tần số góc $5\text{ rad/s}$. Khi vật đi qua li độ $5\text{ cm}$ thì nó có tốc độ là $25\text{ cm/s}$. Biên độ dao động của vật là:

A. $5,24\text{ cm}$                       B. $5\sqrt{2}\ cm$                        C. $5\sqrt{3}\text{ cm}$              D. $10\text{ cm}$

Câu 6 (CĐ-2011): Một vật dao động điều hòa với chu kì 2 s, biên độ 10 cm. Khi vật cách vị trí cân bằng 6 cm thì tốc độ của nó bằng:

A. $12,56\text{ cm/s}$      B. $20,08\text{ cm/s}$      C. $25,13\text{ cm/s}$      D. $18,84\text{ cm/s}$

Câu 7: Một vật dao động điều hòa với biên độ 5 cm. Khi vật có li độ là 4 cm thì vận tốc là $\text{6 }\!\!\pi\!\!\text{ }$  cm/s. Tần số dao động của vật là:

A. $\operatorname{f}=1 Hz$                  B. $\operatorname{f}=1,2 Hz$    C. $\operatorname{f}=3 Hz$                        D. $\operatorname{f}=4,6 Hz$

Câu 8 (ĐH-2011): Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là $20\text{ cm/s}$. Khi chất điểm có tốc độ là $10\text{ cm/s}$ thì gia tốc của nó có độ lớn là $40\sqrt{3}\text{ cm/}{{\text{s}}^{2}}$. Biên độ dao động của chất điểm là:

A. $5\text{ cm}$                 B. $4\text{ cm}$                 C. $10\text{ cm}$               D. $8\text{ cm}$

Câu 9: Một chất điểm dao động điều hòa trên trục Ox với chu kì 2 s và biên độ 9 cm. Tại thời điểm t, lực hồi phục tác dụng lên vật có độ lớn $\operatorname{F}=0,15\ N$ và động lượng của vật lúc đó là $\text{p = 37,5}\sqrt{\text{2}}\text{ gm/s}$. Lấy \[{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}\text{ = 10}\]. Khối lượng của vật nặng là:

A. 0,15 kg                  B. 0,25 kg                  C. 0,12 kg                  D. 0,2 kg

Câu 11: Một con lắc lò xo nằm ngang gồm quả nặng có khối lượng $\operatorname{m}=100\ g$ thực hiện dao động điều hòa. Khi chất điểm ở cách vị trí cân bằng 6 cm thì tốc độ của vật bằng $\text{0,4}\ \text{m/s}$ và lực kéo về tác dụng lên vật có độ lớn bằng 0,15 N. Biên độ dao động chất điểm là:

A. 4cm                       B. $5\sqrt{5}$ cm               C. 5 cm                      D. 10 cm

Câu 12: Một vật dao động điều hòa có vận tốc và tọa độ tại thời điểm ${{t}_{1}}$ và ${{t}_{2}}$ tương ứng là: ${{\operatorname{v}}_{1}}=20 cm/s$, ${{\operatorname{x}}_{1}}=8\sqrt{3} cm$ và ${{\operatorname{v}}_{2}}=20\sqrt{2} cm/s$, ${{\operatorname{x}}_{2}}=8\sqrt{2} cm$. Vận tốc cực đại của vật dao động là:

A. $40\sqrt{2}\text{ cm/s}$        B. $40\text{ cm/s}$                        C. $40\sqrt{3}\text{ cm/s}$        D. $\text{80 cm/s}$

Câu 13: Một chất điểm dao động điều hòa trên trục Ox. Tại thời điểm ${{\operatorname{t}}_{1}}, {{t}_{2}}$ vận tốc và gia tốc của vật có giá trị tương ứng là ${{v}_{1}}=10\sqrt{3}\text{ cm/s, }{{\text{a}}_{1}}=-1\text{ m/}{{\text{s}}^{2}}$ và ${{\text{v}}_{\text{2}}}\text{ = -10 cm/s}$, ${{\text{a}}_{\text{2}}}\text{ = -}\sqrt{\text{3}}\text{ m/}{{\text{s}}^{\text{2}}}$. Li độ tại thời điểm ${{\text{t}}_{\text{2}}}$ của vật là:

A. $-1\text{ cm}$                 B. $\text{1 cm}$                   C. $\frac{1}{\sqrt{3}}\text{ cm}$               D. $\text{3}\ \text{cm}$

Câu 14: Động lượng và gia tốc của một vật nặng 1 kg dao động điều hòa tại các thời điểm ${{\text{t}}_{\text{1}}}\text{, }{{\text{t}}_{\text{2}}}$ có giá trị tương ứng \[{{\operatorname{p}}_{1}} = 0,12\ kgm/s\], ${{\operatorname{p}}_{2}} = 0,16\ kgm/s$, ${{\operatorname{a}}_{1}} = 0,64\ m/{{s}^{2}}$, ${{\operatorname{a}}_{2}} = 0,48\ m/{{s}^{2}}$. Động năng biến thiên với chu kì:

A. $\text{0,25 }\!\!\pi\!\!\text{ }\ \text{s}$                       B. $\text{0,125 }\!\!\pi\!\!\text{ }\ \text{s}$                      C. $\text{0,5 }\!\!\pi\!\!\text{ }\ \text{s}$              D. $\text{0,5}\ \text{s}$

Câu 15: Trong dao động điều hòa, gọi tốc độ và gia tốc tại hai thời điểm khác nhau lần lượt là ${{\text{v}}_{\text{1}}}\text{, }{{\text{v}}_{\text{2}}}$ và ${{\text{a}}_{\text{1}}}\text{, }{{\text{a}}_{\text{2}}}$thì tần số góc được xác định bởi biểu thức nào sau đây là đúng?

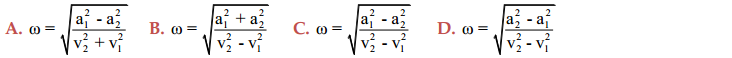
Câu 16: Một vật dao động điều hòa với biên độ A quanh vị trí cân bằng O. Ở vị trí M, vật có li độ ${{\text{x}}_{\text{1}}}$ và tốc độ ${{\text{v}}_{\text{1}}}$. Ở vị trí N, vật có li độ ${{\text{x}}_{\text{2}}}$ và tốc độ ${{\text{v}}_{\text{2}}}$. Biên độ A là:

A. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}}}$   B. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}}}$   C. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ - v}_{\text{2}}^{\text{2}}}}$          D. $\sqrt{\frac{\text{v}_{\text{1}}^{\text{2}}\text{x}_{\text{2}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}\text{x}_{\text{1}}^{\text{2}}}{\text{v}_{\text{1}}^{\text{2}}\text{ + v}_{\text{2}}^{\text{2}}}}$

Câu 17: Một chất điểm dao động điều hòa trên một đoạn thẳng, khi đi qua M và N chất điểm có gia tốc lần lượt là ${{\text{a}}_{\text{M}}}\text{ = 3}\ \text{m/}{{\text{s}}^{\text{2}}}$ và ${{\text{a}}_{\text{N}}}\text{ = 8 m/}{{\text{s}}^{\text{2}}}$. A là một điểm trên đoạn MN và $\text{AM = 3}\text{.AN}$. Gia tốc chất điểm khi đi qua A:

A. $11\text{ m/}{{\text{s}}^{2}}$               B. $5\text{ m/}{{\text{s}}^{2}}$                  C. $\text{2,75 m/}{{\text{s}}^{2}}$              D. $6,75\text{ m/}{{\text{s}}^{2}}$

Câu 18: Li độ và tốc độ của một vật dao động điều hòa liên hệ với nhau theo biểu thức $\frac{{{\text{x}}^{\text{2}}}}{36}\text{ + }\frac{{{\text{v}}^{\text{2}}}}{0,09}\text{ = 1}$. Trong đó $\text{x}$ và $\text{v}$ lần lượt tính theo đơn vị $\text{cm}$và $\text{m/s}$. Biên độ dao động của vật là:

A. 6 cm                      B. 3 cm                      C. 4 cm                      D. 5 cm

Câu 20: Hai vật dao động điều hòa dọc theo các trục song song với nhau. Phương trình dao động của các vật lần lượt là ${{\text{x}}_{\text{1}}}\text{ = }{{\text{A}}_{\text{1}}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t + }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}} \right)\ \left( \text{cm} \right)$và $\text{ }{{\text{x}}_{\text{2}}}\text{ = }{{\text{A}}_{\text{2}}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t + }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{2}}} \right)\text{ }\left( \text{cm} \right)$.Biết $\text{3x}_{\text{1}}^{\text{2}}\text{ + 2x}_{\text{2}}^{\text{2}}\text{ = 50 }\left( \text{c}{{\text{m}}^{\text{2}}} \right)$. Tại thời điểm t, vật thứ hai đi qua vị trí có li độ ${{\operatorname{x}}_{2}}=1 cm $với vận tốc ${{\text{v}}_{\text{2}}}\text{ = 15 cm/s}$. Khi đó vật thứ nhất có tốc độ bằng:

A. $\text{5 cm/s}$                          B. $\text{5}\sqrt{\text{3}}\text{ cm/s}$                     C. $10\ \text{cm/s}$                        D. $2,5\ \text{cm/s}$

 

 

Đáp án:

 

 

Bài viết gợi ý:

1. Bài tập cơ bản tổng hợp dao động điều hòa

2. Bài toán về thời điểm thời gian vật đi qua vị trí có li độ cho trước và bài toán lặp lại trạng thái dao động

3. Xác định các đại lượng đặc trưng của dao động điều hòa

4. Giới thiệu phương trình dao động điều hòa, các hệ thức độc lập với thời gian