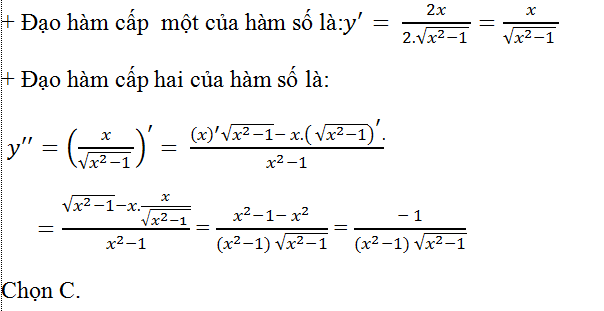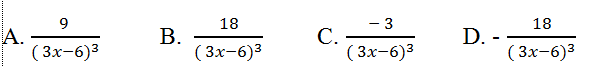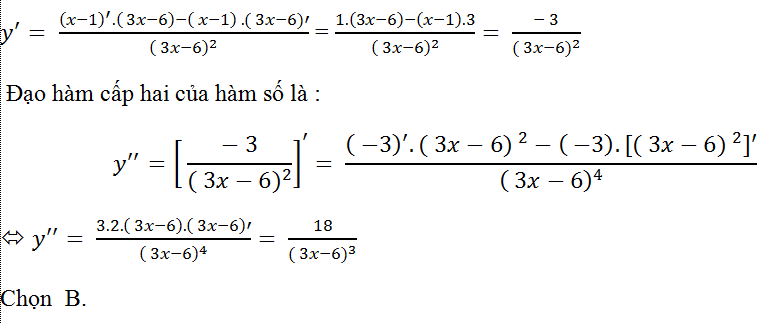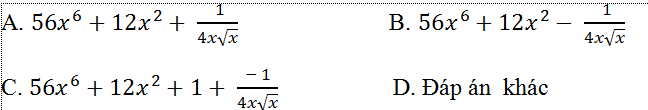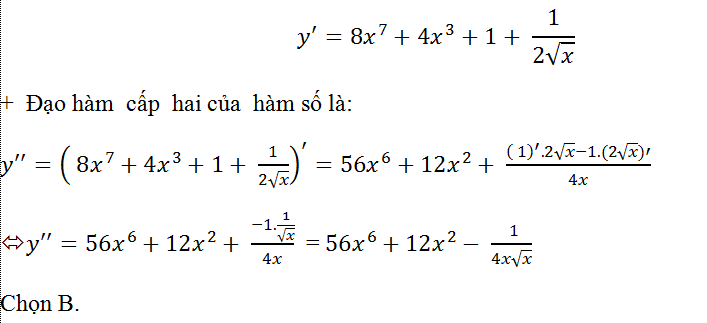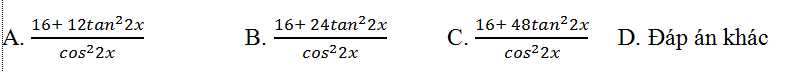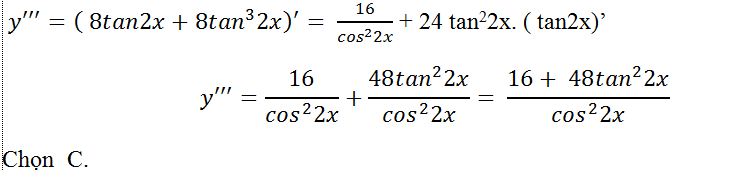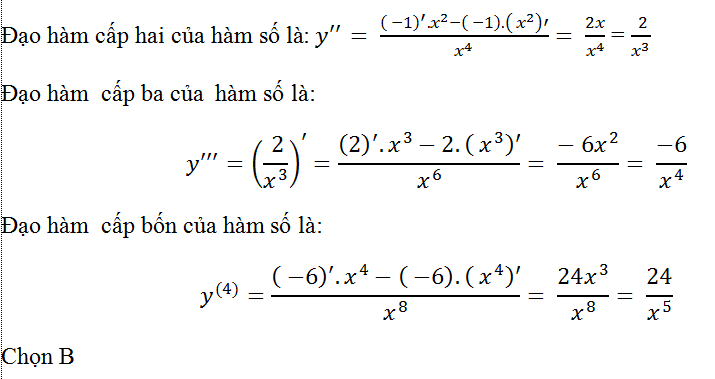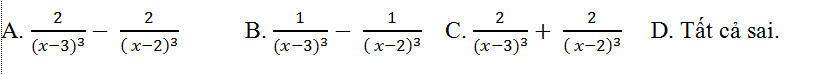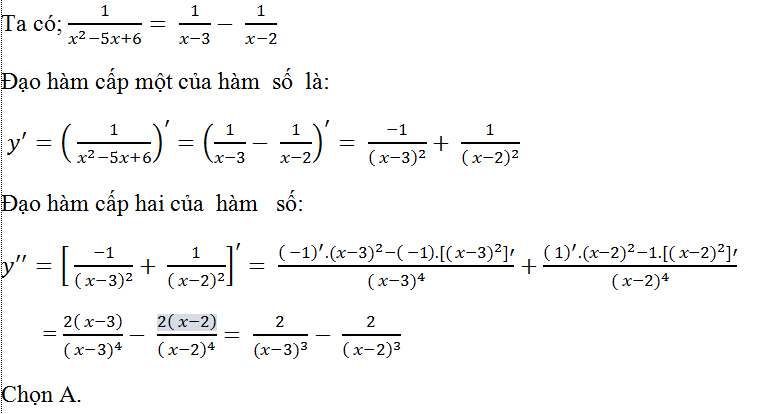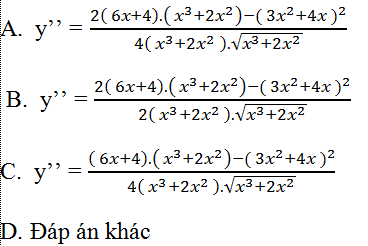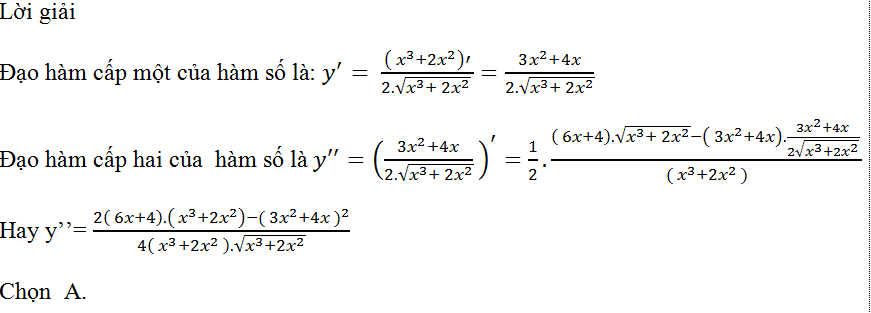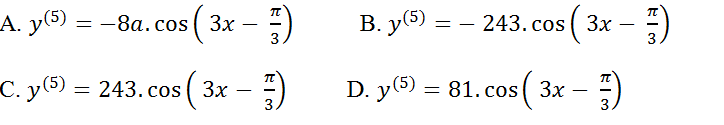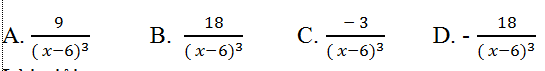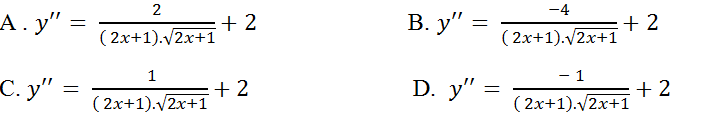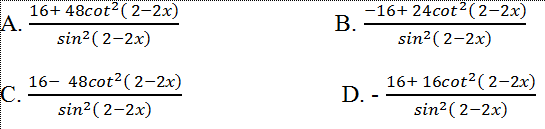Cách Tìm đạo Hàm Cấp Cao Của Hàm Số Hay, Chi Tiết

Cách tìm đạo hàm cấp cao của hàm số hay, chi tiết

A. Phương pháp giải

+ Đạo hàm cấp hai: Cho hàm số y= f(x) có đạo hàm tại trên khoảng (a ;b). Nếu hàm số y’= f’(x) cũng có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp hai của hàm số y= f(x) và được kí hiệu là y'' hay f'' (x), tức là: f''=(f')' .

+Đạo hàm cấp n: Cho hàm số y= f(x) có đạo hàm cấp n-1 (với n thuộc số tự nhiên ,n ≥ 2) là f(n-1)(x). Nếu f(n-1) cũng có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của hàm số

y= f(x) và được kí hiệu là f(n), tức là: f((n) ) (x)=(f((n-1) ) (x))'

B. Ví dụ minh họa

Ví dụ 1. Tính đạo hàm cấp ba của hàm số y= sin (3x – 1)

A. – 27cos( 3x- 1) B. 27.cos(3x- 1)

C. 9.sin( 3x- 1) D.Đáp án khác

Hướng dẫn giải

Đạo hàm cấp một của hàm số đã cho là: y'=3 cos⁡(3x-1)

Đạo hàm cấp hai của hàm số là; y''=[ 3.cos⁡( 3x-1) ]'= -9 sin⁡( 3x-1)

Đạo hàm cấp ba của hàm số là y'''=[ -9 sin⁡(3x-1) ]'= -27 cos⁡(3x-1)

Chọn A.

Ví dụ 2 : Tính đạo hàm cấp ba của hàm số y= ( 2x+ x2)( x2 – 1)

A. 12+ 24x B. 12x2 + 12x- 2 C. 12x+ 24 D. 6x+ 12

Hướng dẫn giải

Ta có: y=( 2x+ x2) ( x2 -1)= 2x3

-2x + x4 – x2

+ Đạo hàm cấp một của hàm số là: y'=6x2-2+4x3-2x

+ Đạo hàm cấp hai của hàm số là: y''=(6x2-2+4x3-2x)'=12x+12x2-2

+ Đạo hàm cấp ba của hàm số là: y'''=( 12x+12x2-2)'=12+24x

Chọn A.

Ví dụ 3: Tính đạo hàm cấp hai của hàm số: y= √(x2-1)

Hướng dẫn giải

Hàm số có đạo hàm khi x > 1 hoặc x < -1( khi đó x2 -1> 0)

Ví dụ 4. Tính đạo hàm cấp hai của hàm số y= cos ( 2x+ x2)

A. - [ cos( 2x+ x2 )( 2+ 2x)2 + 2sin ( 2x+ x2 )]

B. cos( 2x+ x2 )( 2+ 2x)2 + 2sin ( 2x+ x2 )

C. - [ cos( 2x+ x2 )( 2+ 2x)2 - 2sin ( 2x+ x2 )]

D. - [ cos( 2x+ x2 )( 2+ 2x)2 + sin ( 2x+ x2 )]

Hướng dẫn giải

Đạo hàm cấp một của hàm số là:

y'= -sin⁡(2x+ x2 ).( 2x+ x2 )'= -sin⁡( 2x+ x2 ).( 2+2x)

Đạo hàm cấp hai của hàm số là:

y''=[- sin⁡( 2x+ x2 ).( 2+2x)]'

=-{[sin⁡( 2x+ x2 ) ]'.( 2+2x)+sin⁡( 2x+ x2 ).(2+2x)'}

= -{ cos(2x+ x2).(2x+ x2) '( 2+ 2x)+ sin (2x+ x2).2 }

= - [ cos( 2x+ x2 )( 2+ 2x)2 + 2sin ( 2x+ x2 )]

Chọn A.

Ví dụ 5. Tính đạo hàm cấp hai của hàm số y= (x-1)/(3x-6)?

Hướng dẫn giải

Hàm số có đạo hàm tại các điểm x≠2. Khi đó; đạo hàm cấp một của hàm số là

Ví dụ 6. Tính đạo hàm cấp hai của hàm số sau y= x10 + 9x2 + 8x+ 10

A. 90x8 +1 8 B. 10x9 + 18x C. 9x8+ 18 D. Tất cả sai

Hướng dẫn giải

+ Đạo hàm cấp một của hàm số là:

y'= 10x9+ 18x + 8

⇒ Đạo hàm cấp hai của hàm số là:

y''=(10x9+18x+8)' = 90x8+ 18

Chọn A.

Ví dụ 7. Tính đạo hàm cấp hai của hàm số: y= x8+ x4+x+ √x

Hướng dẫn giải

Hàm số có đạo hàm nếu x< 0.

+ Đạo hàm cấp một của hàm số là:

Ví dụ 8 : Tính đạo hàm cấp hai của hàm số: y= sin( 2x- 1) – cos (2x- 4)

A. y’’= - 4sin( 2x- 1)+ 4 cos( 2x-4) B. y’’= - 4sin( 2x- 1)- 4 cos( 2x-4)

C. y’’= 4sin( 2x- 1)- 4 cos( 2x-4) D.y’’= 4sin( 2x- 1)+ 4 cos( 2x-4)

Hướng dẫn giải

Đạo hàm cấp một của hàm số là; y'=2 cos⁡( 2x-1)+2sin⁡( 2x-4)

Đạo hàm cấp hai của hàm số là:

y''=[2 cos⁡( 2x-1)+2 sin⁡( 2x-4)]' = - 4sin( 2x- 1)+ 4 cos( 2x-4)

Chọn A.

Ví dụ 9. Tính đạo hàm cấp ba của hàm số y= tan2x

Hướng dẫn giải

Đạo hàm cấp một của hàm số là: y'=2( 1+tan2 2x )

Đạ hàm cấp hai của hàm số là:

y''=2.( 1+tan2 2x )’= 2.2. tan2x. ( tan2x)’

=4tan2 x( 1+ tan22x) . ( 2x)’= 8tan2x( 1+ tan22x) = 8.tan2x+ 8tan32x

Đạo hàm cấp ba của hàm số là:

Ví dụ 10: Tính đạo hàm cấp bốn của hàm số y= 1/x

Hướng dẫn giải

Hàm số có đạo hàm tại điểm x≠0

Đạo hàm cấp một của hàm số là: y'= (- 1)/x2

Ví dụ 11: Tính đạo hàm cấp hai của hàm số y= 1/(x2-5x+6)

Hướng dẫn giải

Hàm số có đạo hàm tại các điểm x≠2;x≠3

Ví dụ 12: Tính đạo hàm cấp hai của hàm số: y= ( x2+1)3 .

A. 3 .( x2+1) 2+6x2 (x2+1) B. 3 .( x2+1) 2+12x2 (x2+1)

C. 6 .( x2+1) 2-12x2 (x2+1) D. 6 .( x2+1) 2+24x2 (x2+1)

Hướng dẫn giải

Đạo hàm cấp một của hàm số là: y'=3(x2+1) 2.(x2+1)^'=6x.( x2+1) 2

Đạo hàm cấp hai của hàm số là:

y''=6 .( x2+1) 2+6x.[( x2+1) 2]'

= 6 .( x2+1) 2+6x.2(x2+1).( x2+1)'

= 6 .( x2+1) 2+24x2 (x2+1)

Chọn D.

Ví dụ 13 : Tính đạo hàm cấp hai của hàm số y= √(x3+ 2x2 )

Hướng dẫn giải

C. Bài tập vận dụng

Câu 1: Cho hàm số: y=sin⁡(3x- π/3). Tính đạo hàm cấp năm của hàm số

Câu 2: Tính đạo hàm cấp hai của hàm số y= (x+3)/(x-6)?

Câu 3: Tính đạo hàm cấp ba của hàm số y= (x3 – 1) (x+1)

A. 12+ 24x B. 24x+ 6 C. 12x+ 24 D. 24x+ 12

Câu 4: Tính đạo hàm cấp hai của hàm số: y=x.sinx

A. cosx + x. sinx B. 2sinx+ x. cosx

C. 2cosx- x. sinx D. Đáp án khác

Câu 5: Tính đạo hàm cấp hai của hàm số y = cos( x2+x+ 1)

A. y''= -cos⁡( x2+x+1).( 2x+1) 2 – 2 sin( x2 + x+ 1)

B. y''= cos⁡( x2+x+1).( 2x+1) 2 + 2 sin( x2 + x+ 1)

C. y''= -cos⁡( x2+x+1).( 2x+1) 2 - sin( x2 + x+ 1)

D. Tất cả sai

Câu 6: Tính đạo hàm cấp 4 của hàm số; y=(x2+x+1)/(x+1)

Câu 7: Tính đạo hàm cấp hai của hàm số: y= 3cos( x+ 1) - 8. sin( 3x+ 10)

A. y''= -3 cos⁡( x+1)+72 sin⁡( 3x+10)

B. y''= -3 cos⁡( x+1)+36 sin⁡( 3x+10)

C.y''= -3 cos⁡( x+1) -72sin⁡( 3x+10)

D. tất cả sai

Câu 8: Tính đạo hàm cấp hai của hàm số: y= ( x3+2x-1)2 .

A. y''=( 3x2+2)( 6x2+4)- ( x3+2x-1).12x

B. y''=( 3x2+2)( 3x2+2)+( x3+2x-1).12x

C. y''=( 3x2+2)( 6x2+4)+( x3+2x-1).12x

D. Tất cả sai

Câu 9: Tính đạo hàm cấp ba của hàm số sau y= x9 – x4 + 8x2+ 3

A. 504x6 - 24x B. 72x6 - 24x+ 3 C. 72x7 - 24x+ 3 D. Tất cả sai

Câu 10: Tính đạo hàm cấp hai của hàm số: y= x7-2x2+9x+ 2√x

Câu 11: Tính đạo hàm cấp hai của hàm số y= √(2x+1)+x2

Câu 12: Tính đạo hàm cấp ba của hàm số y=2 cos ( 10- 2x)

A. –16 sin( 10- 2x) B. – 16 cos( 10- 2x)

C. - 8.sin( 10- 2x) D.Đáp án khác

Câu 13: Tính đạo hàm cấp hai của hàm số y= sin ( x2- 9)

A. 4x2. sin( x2 – 9) - 2.cos( x2 – 9)

B. - 2x2. sin( x2 – 9)+ 2.cos( x2 – 9)

C. - 4x2. sin( x2 – 9)+ 2.cos( x2 – 9)

D. Đáp án khác

Câu 14: Tính đạo hàm cấp ba của hàm số y=cot( 2- 2x)

Câu 15: Tính đạo hàm cấp ba của hàm số y= 1/(2x-2)