Cách Tìm Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số Lượng Giác
Có thể bạn quan tâm
Trong nội dung bài này, chúng ta tập trung vào một số bài tập tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác, vì hàm số lượng giác có tập nghiệm phức tạp và dễ gây nhầm lẫn cho rất nhiều em.
I. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - kiến thức cần nhớ
• Cho hàm số y = f(x) xác định trên tập D ⊂ R.
- Nếu tồn tại một điểm x0 ∈ X sao cho f(x) ≤ f(x0) với mọi x ∈ X thì số M = f(x0) được gọi là giá trị lớn nhất của hàm số f trên X.
Ký hiệu: 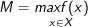
- Nếu tồn tại một điểm x0 ∈ X sao cho f(x) ≥ f(x0) với mọi x ∈ X thì số m = f(x0) được gọi là giá trị nhỏ nhất của hàm số f trên X.
Ký hiệu: 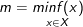

II. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác
* Phương pháp tìm GTLN và GTNN của hàm số lượng giác
+ Để tìm Max (M), min (m) của hàm số y = f(x) trên [a;b] ta thực hiện các bước sau:
- Bước 1: Tính f'(x), tìm nghiệm f'(x) = 0 trên [a;b].
- Bước 2: Tính các giá trị f(a); f(x1); f(x2);...; f(b) (xi là nghiệm của f'(x) = 0)
- Bước 3: So sánh rồi chọn M và m.
> Lưu ý: Để tìm M và m trên (a;b) thì thực hiện tương tự như trên nhưng thay f(a) bằng 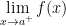 và f(b) bằng
và f(b) bằng 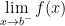 (Các giới hạn này chỉ để so sáng khong chọn làm GTLN và GTNN).
(Các giới hạn này chỉ để so sáng khong chọn làm GTLN và GTNN).
• Nếu f tăng trên [a;b] thì M = f(b), m = f(a).
• Nếu f giảm trên [a;b] thì m = f(b), M = f(a).
• Nếu trên D hàm số liên tục và chỉ có 1 cực trị thì giá trị cực trị đó là GTLN nếu là cực đại, là GTNN nếu là cực tiểu.
* Bài tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm lượng giác sau:
y = sinx.sin2x trên [0;π]
* Lời giải:
- Ta có f(x) = y = sinx.sin2x
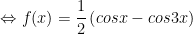
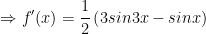
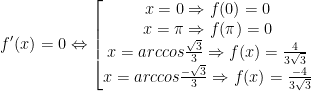
Vậy 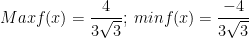
* Bài tập 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm y = sinx + cosx trong đoạn [0;2π].
* Lời giải:
- Ta có: f(x) = y = sinx + cosx ⇒ f'(x) = cosx - sinx
f'(x) = 0 ⇔ cosx = sinx ⇔ x = π/4 hoặc x = 5π/4
- Như vậy, ta có:
f(0) = 1; f(2π) = 1;
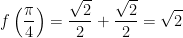 ;
;
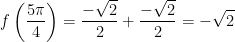
Vậy 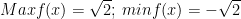
• Cách khác:
f(x) = sinx + cosx = √2.sin(x + π/4)
Vì -1 ≤ sin(x + π/4) ≤ 1 nên -√2 ≤ √2.sin(x + π/4) ≤ √2.
Nên 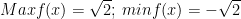
* Bài tập 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y= 3sinx+ 4cosx + 1
* Lời giải:
- Với bài này ta có thể áp dụng bất đẳng thức sau:
(ac + bd)2 ≤ (c2 + d2)(a2 + b2) dấu "=" xảy ra khi a/c = b/d
- Vậy ta có: (3sinx+ 4cosx)2 ≤ (32 + 42)(sin2x + cos2x) = 25
Suy ra: -5 ≤ 3sinx+ 4cosx ≤ 5
⇒ -4 ≤ y ≤ 6
Vậy Maxy = 6 đạt được khi tanx = 3/4
miny = -4 đạt được khi tanx = -3/4.
> Nhận xét: Cách làm tương tự ta có được kết quả tổng quát sau:
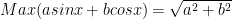 và
và 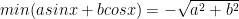
Tức là: 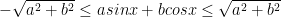
* Bài tập 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3cosx + sinx - 2
* Lời giải:
- Bài này làm tương tự bài 3 ta được: 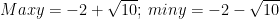
* Bài tập 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y = 3cosx + 2
* Lời giải:
- Ta có: -1 ≤ cosx ≤ 1 ∀x ∈ R.
Maxy = 3.1 + 1 = 4 khi cosx = 1 ⇔x = k2π
Minxy = 3.(-1) + 1 = -2 khi cosx = -1 ⇔x = π + k2π
* Bài tập 6: Tìm m để phương trình: m(1 + cosx)2 = 2sin2x + 2 có nghiệm trên [-π/2;π/2].
* Lời giải:
- Phương trình trên tương đương: 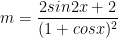 (*)
(*)
Đặt ![t=tan\frac{x}{2}\in [-1,1],\: \forall x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1607504012cp8dynyta1_1622534188.gif)
khi đó: 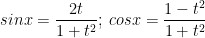
(*) ⇔ t4 - 4t3 + 2t2 + 4t + 1 = 2m.
Xét f(t) = t4 - 4t3 + 2t2 + 4t + 1 trên đoạn [-1;1]
Ta có: f'(t) = 4t3 - 12t2 + 4t + 4 = 0 ⇔ t = 1; t = 1 - √2; t = 1 + √2(loại)
Có: f(-1) = 1 + 4 + 2 - 4 + 1 = 4
f(1) = 1 - 4 + 2 + 4 + 1 = 4
f(1 - √2) = (1 - √2)4 - 4(1 - √2)3 + 2(1 - √2)2 + 4(1 - √2) + 1 = 0
Ta được: Minf(t) = 0; Maxf(t) = 4
Để phương trình có nghiệm ta phải có 0 ≤ 2m ≤ 4.
Vậy 0 ≤ m ≤ 2 thì phương trình có nghiệm.
III. Bài tập Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác tự làm
* Bài tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác: 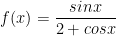 trên [0;π].
trên [0;π].
* Đáp số bài tập 1:
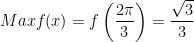 ;
;
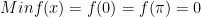
* Bài tập 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác: f(x) = 2cos2x - 3cosx - 4 trên [-π/2;π/2].
* Đáp số bài tập 2:
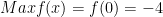
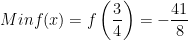
* Bài tập 3: Tìm giá trị lớn nhất của hàm số: f(x) = x + 2cosx trên (0;π/2).
* Đáp số bài tập 3:
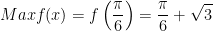 ;
;
* Bài tập 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác: f(x) = 2sin2x + 2sinx - 4.
* Đáp số bài tập 4:
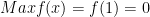
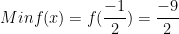
* Bài tập 5: Tìm giá trị lớn nhất của hàm số: y = x + sin2x trên [-π/2;π/2].
* Đáp số bài tập 5:
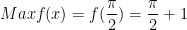
Từ khóa » Tìm Max Của Hàm Số Lượng Giác
-
Tìm Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số Lượng Giác (có Lời ...
-
Cách Tìm Giá Trị Lớn Nhất, Nhỏ Nhất Của Hàm Số Lượng Giác Cực Hay
-
Tìm Giá Trị Lớn Nhất Và Và Giá Trị Nhỏ Nhất Của Hàm Số Lượng Giác
-
Giải Nhanh Trắc Nghiệm Max - Min Hàm Số Lượng Giác – Toán 11
-
Tập Giá Trị Và GTLN - GTLN Của Hàm Số Lượng Giác
-
Tìm Giá Trị Lớn Nhất Nhỏ Nhất Của Hàm Số Lượng Giác - Toán Thầy Định
-
Hàm Số Lượng Giác Lớp 11 Nâng Cao- Đi Sâu Vào Bài Toán Tìm GTLN ...
-
Các Dạng Bài Tập Tìm Max Và Min Của Hàm Số Lượng Giác - Icongchuc
-
[Dạng Bài] Tìm Giá Trị Lớn Nhất, Nhỏ Nhất Của Hàm Số Lượng Giác
-
Tìm Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số Lượng Giác
-
Tập Giá Trị Và GTLN – GTNN Của Hàm Số Lượng Giác - Tài Liệu Tự Học ...
-
Tìm Gtln, Gtnn Của Hàm Số Lượng Giác Lớp 10
-
Giá Trị Nhỏ Nhất Và Lớn Nhất Của Lượng Giác - Phothongonline
-
Tìm Gtln Gtnn Của Hàm Số Lượng Giác Trên đoạn - 123doc