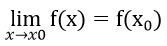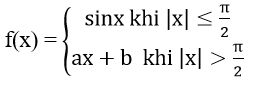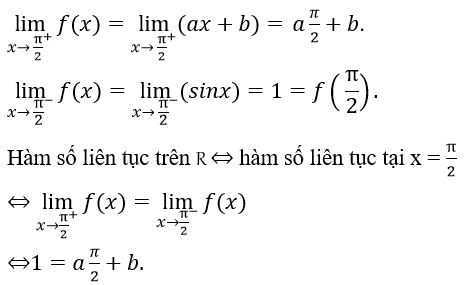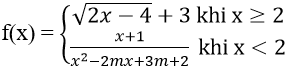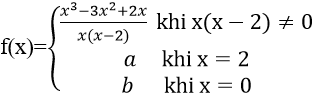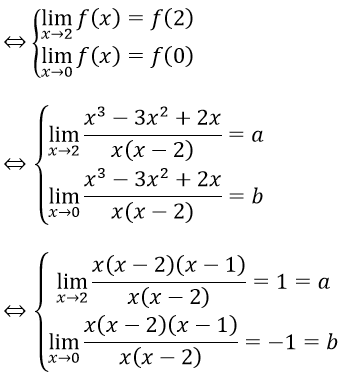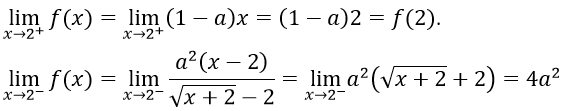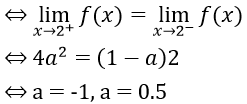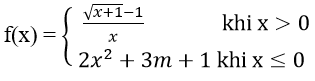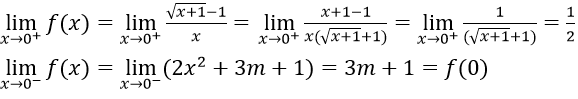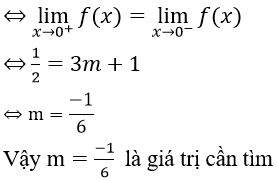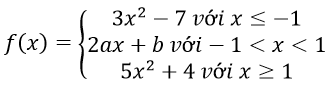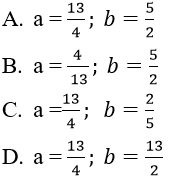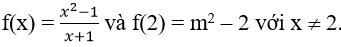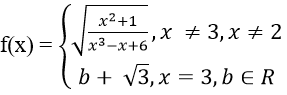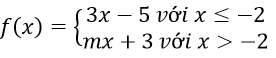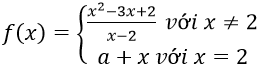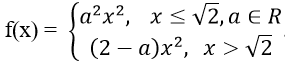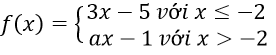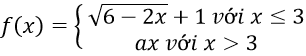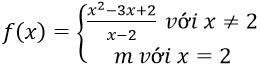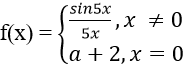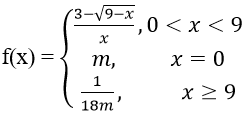Cách Tìm M để Hàm Số Liên Tục Cực Hay

Cách tìm m để hàm số liên tục cực hay

A. Phương pháp giải & Ví dụ

Ta sử dụng điều kiện để hàm số liên tục và điều kiện để phương trình có nghiệm để làm các bài toán dạng này.

- Điệu kiện để hàm số liên tục tại x0:

- Điều kiện để hàm số liên tục trên một tập D là f(x) liên tục tại mọi điểm thuộc D.

- Phương trình f(x) = 0 có ít nhất một nghiệm trên D nếu hàm số y = f(x) liên tục trên D và có hai số a, b thuộc D sao cho f(a).f(b) < 0.

Phương trình f(x) = 0 có k nghiệm trên D nếu hàm số y = f(x) liên tục trên D và tồn tại k khoảng rời nhau (ai ; ai+1) (i = 1,2,…,k) nằm trong D sao cho f(ai).f(ai+1) < 0.

Ví dụ minh họa

Bài 1: Chứng minh rằng phương trình sau có ít nhất một nghiệm :

x7 + 3x5 - 1 = 0

Hướng dẫn:

Ta có hàm số f(x) = x7 + 3x5 - 1 liên tục trên R và f(0).f(1) = - 3 < 0

Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0,1).

Bài 2: Chứng minh rằng phương trình sau có ít nhất một nghiệm :

x2sinx + xcosx + 1 = 0

Hướng dẫn:

Ta có hàm số f(x) = x2sinx + xcosx + 1 liên tục trên R và f(0).f(π) = -π < 0. Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0 ; π).

Bài 3: Xác định a, b để các hàm số sau liên tục trên R

Hướng dẫn:

Ta có hàm số đã cho liên tục trên R\{π/2} do các hàm y = sinx và y = ax + b lên tục trên R.

Ta chỉ cần xét tính liên tục của hàm số tại x = π/2.

Vậy a, b là số thực thỏa mãn phương trình 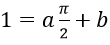thì hàm số đã cho liên tục trên R.

Bài 4: Tìm m để các hàm số sau liên tục trên R

Hướng dẫn:

Hàm số xác định trên R

Với x < 2 ⇒ hàm số liên tục

Với x > 2 ⇒ hàm số liên tục

Với x = 2 ta có

⇔ m = 3

Vậy m = 3 là giá trị cần tìm

Bài 5: Xác định a,b để các hàm số sau liên tục trên R

Hướng dẫn:

Với x ≠ 2 và x ≠ 0 hàm số liên tục.

Để hàm số đã cho liên tục trên R thì hàm số phải liên tục tại x = 2 và x = 0

Vậy a = 1 và b = -1 thì hàm số liên tục trên R

Bài 6: Xác định a để hàm số 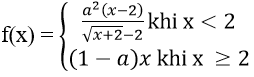liên tục trên R.

Hướng dẫn:

Hàm số xác định trên R

Với x < 2 ⇒ hàm số liên tục

Với x > 2 ⇒ hàm số liên tục

Với x = 2 ta có

Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 2

Vậy a = -1, a = 0.5 là những giá trị cần tìm.

Bài 7: Cho hàm số f(x) = x3 – 1000x2 + 0,01 . phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây ?

I. (–1; 0) II. (0; 1) III. (1; 2)

Hướng dẫn:

Ta có hàm số y = f(x) = x3 – 1000x2 + 0,01 là hàm liên tục trên R

f(0) = 0.01 và f(-1) = - 1001 + 0.01 < 0. Nên f(0).(-1) < 0.

Vậy hàm số có nghiệm trong khoảng I

Bài 8: Tìm m để các hàm số sau liên tục trên R

Hướng dẫn:

Với x < 0 ⇒ hàm số liên tục

Với x > 0 ⇒ hàm số liên tục

Với x = 0 ta có

Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 0

B. Bài tập vận dụng

Bài 1: Cho hàm số:

Hàm số đã cho liên tục trên R khi và chỉ khi:

Bài 2: Cho hàm số

Giá trị của m để f(x) liên tục tại x = 2 là:

Bài 3: Cho hàm số:

Tìm b để f(x) liên tục tại x = 3

A. √3 B. - √3 C. (2√3)/3 D. – (2√3)/3

Bài 4: Cho hàm số:

Giá trị nào của m để hàm số đã cho liên tục tại x = -2?

A. 7

B. -7

C. 5

D. 1

Bài 5: Cho hàm số:

Với giá trị nào của a thì hàm số đã cho liên tục tại x = 2?

A. -2

B. -1

C. 1

D. 3

Bài 6: Tìm khẳng định đúng trong các khẳng định sau:

I. f(x) liên tục trên đoạn [a;b] và f(a).f(b) > 0 thì tồn tại ít nhất số c ∈ (a;b) sao cho f(c) = 0

II. f(x) liên tục trên (a;b] và trên [b;c) nhưng không liên tục trên (a;c)

A. Chỉ I đúng B. Chỉ II đúng C. Cả I và II đúng D. Cả I và II sai

Bài 7: Tìm khẳng định đúng trong các khẳng định sau:

I. f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0 thì phương trình f(x) = 0 có nghiệm

II. f(x) không liên tục trên [a;b] và f(a).f(b) ≥ 0 thì phương trình f(x) = 0 vô nghiệm

A. Chỉ I đúng B. Chỉ II đúng C. Cả I và II đúng D. Cả I và II sai

Bài 8: Cho hàm số 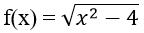. Chọn câu đúng trong các câu sau:

(I) f(x) liên tục tại x = 2

(II) f(x) gián đoạn tại x = 2

(III) f(x) liên tục trên đoạn [-2, 2]

A. Chỉ (I) và (III) B. Chỉ (I) C. Chỉ (II) D. Chỉ (II) và (III)

Bài 9: Cho hàm số:

Giá trị của a để f(x) liên tục trên R là:

A. 1 và 2 B. 1 và –1 C. –1 và 2 D. 1 và –2

Bài 10: Cho hàm số:

Với giá trị nào của a thì hàm số f(x) liên tục tại x = - 2?

A. a = -5

B. a = 0

C. a = 5

D. a = 6

Bài 11: Cho hàm số:

Với giá trị nào của a thì hàm số f(x) liên tục tại x = 3?

A. a = 3 B. a = 1/3 C. a = -1/3 C. a = -2

Bài 12: Cho hàm số:

Với giá trị nào của m thì hàm số đã cho liên tục tại x = 2?

A. -2

B. -1

C. 1

D. 3

Bài 13: Cho hàm số:

Tìm a để f(x) liên tục tại x = 0

A. 1 B. –1 C. –2 D. 2

Bài 14: Cho hàm số:

Tìm k để f(x) gián đoạn tại x = 1.

Bài 15: Cho hàm số:

Tìm m để f(x) liên tục trên [0;+∞) là.

A.1/3 B. 1/2 C. 1/6 D. 1