Cách Tìm Nguyên Hàm Của Hàm Số F(x) Và Bài Tập Vận Dụng - Hayhochoi
Có thể bạn quan tâm
Vậy tìm nguyên hàm của hàm số f(x) như thế nào? Bài viết này chúng ta sẽ cùng tìm hiểu phương pháp tìm nguyên hàm của hàm số sau đó vận dụng vào các bài tập minh họa tìm nguyên hàm để các em dễ hiểu hơn. Để thuận tiện việc giải các bài tập tìm nguyên hàm các em cần nhớ một số công thức tính nguyên hàm sau:
I. Công thức nguyên hàm của các hàm sơ cấp
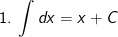
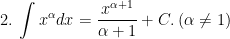
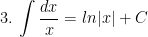
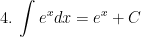
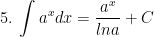
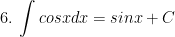
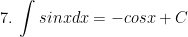
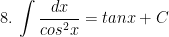
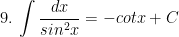
II. Công thức nguyên hàm của các hàm hợp
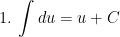
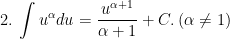
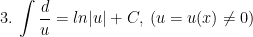
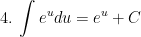
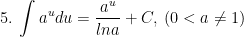
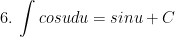
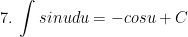
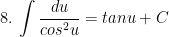
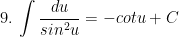
> Lưu ý: trong các công thức trên thì ham u = u(x) là hàm theo biến x.
III. Bài tập Tìm nguyên hàm của hàm f(x)
* Phương pháp tìm nguyên hàm của hàm f(x)
- Phân tích f(x) thành tổng (hiệu) của các hàm số sơ cấp cơ bản (có công thức tính nguyên hàm như ở trên), tính nguyên hàm của từng hàm số rồi suy ra kết quả.
- Dùng các phương pháp đổi biến số hoặc phương pháp nguyên hàm từng phần
>> Xem thêm: Cách tính nguyên hàm bằng phương pháp đổi biến số
>> Xem thêm: Cách tính nguyên hàm bằng phương pháp nguyên hàm từng phần
* Bài tập minh họa tìm nguyên hàm của hàm số f(x)
* Bài tập 1: Tìm họ nguyên hàm của:
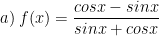
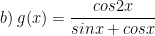
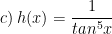
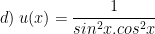
* Lời giải:
a) Ta có:
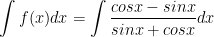
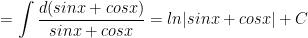
> Lưu ý: d(u) = u'(x)dx.
Ví dụ: d(sinx + cosx) = (sinx + cosx)'dx = (cosx - sinx)dx.
b) Ta có:
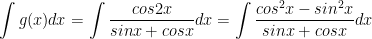
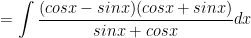
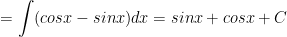
c) Ta có:
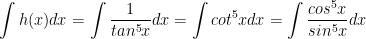
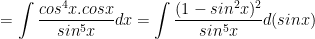
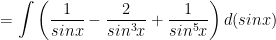
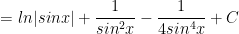
d) Ta có:
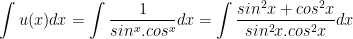
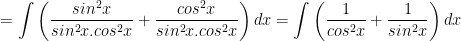
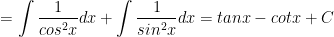
> Lưu ý: Các bước làm ở trên có thể dài dòng với một số bạn, tuy nhiên HayHocHoi mong muốn các bạn hiểu rõ từng bước biến đổi vừa để ôn lại công thức vừa dễ dàng hiểu rõ hơn. Sau khi đã nhuần nhuyễn các công thức bước làm, các em có thể làm gọn hơn đặc biệt là khi làm trắc nghiệm.
* Bài tập 2: Tìm nguyên hàm các hàm sau:
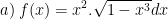
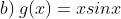
* Lời giải:
a) Ta có: 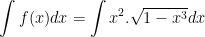
- Ta sử dụng phương pháp đổi biến số:
Đặt u = 1 - x3 ⇒ du = -3x2dx ⇒ x2dx = -(1/3)du. Khi đó ta được:
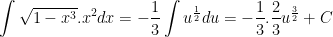
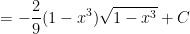
b) Ta có: 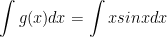
- Ta sử dụng phương pháp nguyên hàm từng phần:
Đặt u = x; dv = sinxdx thì du = dx; v = -cosx. Khi đó theo công thức nguyên hàm:
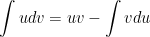
Thì ta được:
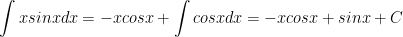
* Bài tập 3: Tìm nguyên hàm của các hàm số f(x) sau:
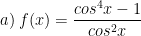
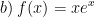
* Lời giải:
a) Ta có:
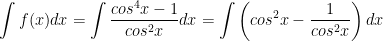
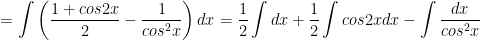
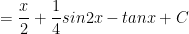
b) Ta có:
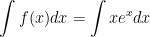
- Dùng phương pháp nguyên hàm từng phần
Đặt u = x ⇒ du = dx; dv = exdx ⇒ v = ex khi đó vận dụng công thức nguyên hàm từng phần ta được:
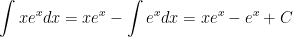
* Bài tập 4. Cho f(x) = cos4x - sin4x. Tìm nguyên hàm của hàm F(x) biết rằng F(π/6) = 0.
* Lời giải:
- Ta có: f(x) = cos4x - sin4x = (cos2x - sin2x)(cos2x + sin2x) = cos2x - sin2x = cos2x
Do đó: 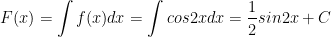
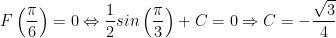
Vậy 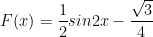
* Bài tập 5: Cho hàm 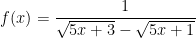 . Tìm nguyên hàm F(x) biết F(0) = 0.
. Tìm nguyên hàm F(x) biết F(0) = 0.
* Lời giải:
- Ta nhân tử và mẫu của f(x) với 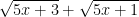 ta được
ta được
![f(x)=\frac{\sqrt{5x+3}+\sqrt{5x+1}}{2}=\frac{1}{2}\left [ (5x+3)^{\frac{1}{2}}+(5x+1)^{\frac{1}{2}} \right ]](https://hayhochoi.vn/uploads/news/wyswyg/2020_12/1607748351j6t0sae9vl.gif)
Do đó: ![F(x)=\int f(x)dx=f(x)=\frac{1}{2}\int \left [ (5x+3)^{\frac{1}{2}}+(5x+1)^{\frac{1}{2}} \right ]dx](https://hayhochoi.vn/uploads/news/wyswyg/2020_12/16077483573ubwd9kjof.gif)
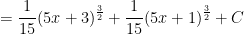
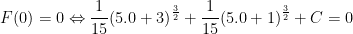
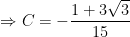
Vậy 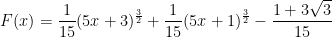
> Nhận xét: Như vậy với bài tập 4 và bài tập 5 là một dạng khác với các bài 1,2,3. Ở bài tập 4,5 yêu cầu chúng ta tìm nguyên hàm của hàm số f(x) thỏa điều kiện cho trước. Việc này chúng ta cũng làm tương tự là tìm họ nguyên hàm F(x) trước. Sau đó dựa vào yêu cầu bài toán (giả thiết) để suy ra giá trị của C.
IV. Bài tập tìm nguyên hàm của hàm số f(x) học sinh tự làm
* Bài tập 1: Tìm nguyên hàm của hàm 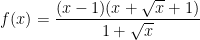
* Đáp án bài tập 1:
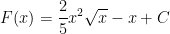
* Bài tập 2: Cho 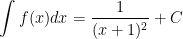 , tìm f(x).
, tìm f(x).
* Đáp án bài tập 2:
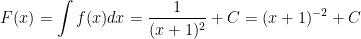
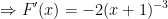 nên
nên 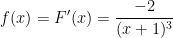
* Bài tập 3: Cho 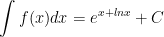 . Tìm f(x)
. Tìm f(x)
* Đáp án bài 3:
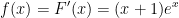
Từ khóa » Hàm Số Fx
-
F(X) Là Gì - Khái Niệm Hàm Số, Trắc Nghiệm Toán Học Lớp 10
-
F(x) Là Gì - Khái Niệm Hàm Số
-
Bài 1 : KHÁI NIỆM HÀM SỐ | Toán Học Phổ Thông
-
Biết được đồ Thị Của Hàm Số F(x) Tìm (số điểm) Cực Trị Của Hàm ẩn
-
Cho Hàm Số F(x) Hoặc F'(x), Tìm điểm Cực Trị, Giá Trị Cực Trị
-
Đồ Thị Hàm Số Y = F'(x) - Phạm Văn Đức
-
Hàm Số – Wikipedia Tiếng Việt
-
Hàm Số Fx - Bài 1
-
Cho Hàm Số F(x) Có F(0)=0. Biết Y=F(x) Là...
-
[LỜI GIẢI] Cho Hàm Số Fx = 12log 2 2x1 - X Tính Tổng S = F 1201
-
Hàm Số F X Là Một Nguyên Hàm Của Hàm Số Fx Trên Khoả - Tự Học 365
-
Thầy Đặng Thành Nam - [ NH-TP ] Dạng Bài: Tìm Hàm Số F(x) Khi Biết ...
-
Cho Hàm Số F(x) Xác định Trên (0;+
-
Câu Hỏi Cho Hàm Số Y = F X Có Tập Xác định Là [ – 33 ] Và đ