Cách Tính Chu Vi Và Diện Tích Hình Chữ Nhật
Có thể bạn quan tâm

Mục Lục
- Công thức tính chu vi hình chữ nhật
- Công thức tính diện tích hình chữ nhật
- Tính Chất Và Dấu Hiệu Nhận Biết Hình Chữ Nhật
- Công Thức Suy Rộng
- Lỗi Sai Hay Gặp Phải Và Những Lưu Ý Khi Làm Bài Tính Diện Tích Hình Chữ Nhật
- Một Số Bài Toán Tính Diện Tích Hình Chữ Nhật
- Cách tính chiều dài hình chữ nhật khi biết diện tích và chu vi hình chữ nhật
- Cho ví dụ
- Bài tập áp dụng
- Bài luyện tập tính chu vi, diện tích hình chữ nhật
Công thức tính chu vi hình chữ nhật
Chu vi hình chữ nhật được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích.
Chu vi hình chữ nhật bằng 2 lần tổng của chiều dài và chiều rộng.
Trong đó:
- P là chu vi hình chữ nhật.
- a là chiều dài hình chữ nhật.
- b là chiều rộng hình chữ nhật.
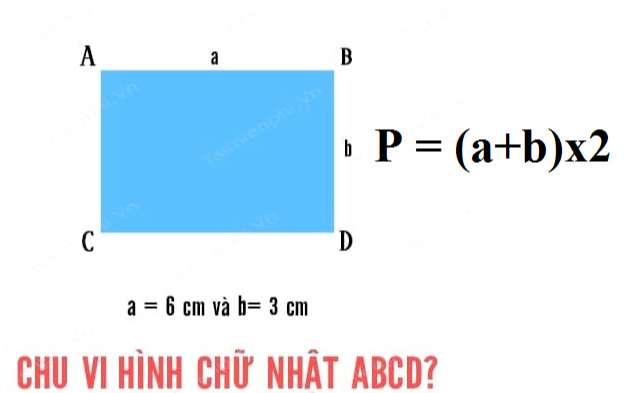
– Ví dụ: Cho một hình chữ nhật ABCD có chiều dài = 6cm và chiều rộng = 3cm. Yêu cầu: Tính chu vi hình chữ nhật ABCD?Với bài toán tính chu vi hình chữ nhật khá đơn giản này, người giải chỉ cần áp dụng công thức tính chu vi hình chữ nhật đã giới thiệu ở trên để giải quyết:Áp dụng công thức tính chu vi hình chữ nhật, ta có: P = (a + b) x 2 = (6 + 3) x 2 = 9×2 = 18 cm .
Công thức tính diện tích hình chữ nhật
Diện tích hình chữ nhật được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình chữ nhật.
Diện tích hình chữ nhật được tính theo công thức chiều dài nhân chiều rộng.
Trong đó:
- S là diện tích hình chữ nhật.
- a là chiều dài hình chữ nhật.
- b là chiều rộng hình chữ nhật.
Trường hợp 1: Biết chiều dài, chiều rộng
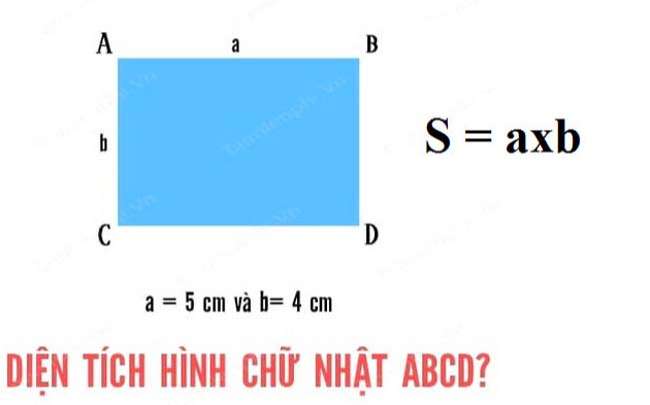
– Khái niệm tính diện tích hình chữ nhật : Diện tích hình chữ nhật bằng tích của chiều dài nhân với chiều rộng.– Công thức tính diện tích hình chữ nhật : S = a x bTrong đó:+ a: Chiều dài của hình chữ nhật+ b: Chiều rộng của hình chữ nhật+ S: diện tích hình chữ nhậtVí dụ: Có một hình chữ nhật ABCD với chiều dài = 5cm và chiều rộng = 4cm. Hỏi diện tích hình chữ nhật ABCD bằng bao nhiêu? Khi áp dụng công thức tính diện tích hình chữ nhật, ta có như sau:S = a x b = 5 x 4 = 20cm2 (Xăng-ti-mét vuông)
* Trường hợp 2: Biết 1 cạnh và đường chéo của hình chữ nhật
Đối với trường hợp này, bạn cần phải tính một cạnh còn lại, sau đó bạn dựa vào công thức ở trường hợp 1 để tính diện tích.
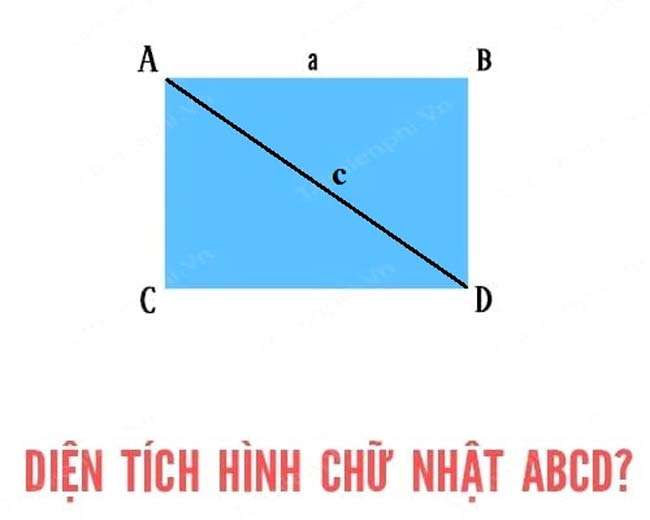
Giả sử: Bài toán cho hình chữ nhật ABCD, biết AB = a, đường chéo AD = c. Tính diện tích ABCD.
– Bước 1: Tính cạnh BD dựa theo định lý Pytago khi xét tam giác vuông ABD.– Bước 2: Biết được cạnh BD và AB thì bạn dễ dàng tính được diện tích ABCD = AB x BD.
Tính Chất Và Dấu Hiệu Nhận Biết Hình Chữ Nhật
* Tính chất
– Hai đường chéo trong hình chữ nhật bằng nhau, cắt nhau tại trung điểm của mỗi đường.– Có đầy đủ tính chất của hình bình hành và hình thang cân.– Hai đường chéo trong hình chữ nhật cắt nhau tạo ra 4 tam giác cân.
* Dấu hiệu
– Tứ giác có 3 góc vuông – Hình thang cân có một góc vuông– Hình bình hành có một góc vuông hoặc có hai đường chéo bằng nhau
Công Thức Suy Rộng
Từ công thức tính diện tích, chu vi hình chữ nhật ở trên, bạn dễ dàng suy ngược công thức tính chiều dài, chiều rộng khi biết được diện tích, chu vi, 1 cạnh:
* Cho diện tích, chiều dài 1 cạnh
– Biết chiều rộng: Chiều dài = Diện tích : Chiều rộng– Biết chiều dài: Chiều rộng = Diện tích : Chiều dài
* Cho chu vi, chiều dài 1 cạnh
– Biết chiều rộng: Chiều dài = P: 2 – chiều rộng– Biết chiều dài: Chiều rộng = P: 2 – chiều dài
Lỗi Sai Hay Gặp Phải Và Những Lưu Ý Khi Làm Bài Tính Diện Tích Hình Chữ Nhật
– Các đại lượng cần phải cùng đơn vị đo lường. Thông thường, các bài toán đơn giản, đề bài sẽ ra đơn vị đo lường giống nhau, còn bài toán khó thì bạn cần chú ý điều này bởi có thể đề bài đánh lừa.– Ghi sai đơn vị tính: Với diện tích, bạn cần viết đơn vị đo lường cùng với mũ 2.
Một Số Bài Toán Tính Diện Tích Hình Chữ Nhật
Bài 6 trang 118 sgk toán lớp 8 tập 1
Câu hỏi:Diện tích hình chữ nhật thay đổi như thế nào nếu:a) Chiều dài tăng 2 lần, chiều rộng không đổi?b) Chiều dài và chiều rộng tăng 3 lần?c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần ?
Lời giải: Công thức tính diện tích hình chữ nhật là S = a.b, như vậy diện tích S của hình chữ nhật vừa tỉ lệ thuận với chiều dài a, vừa tỉ lệ thuận với chiều rộng b của nó.

Bài 7 trang 118 sgk toán lớp 8 tập 1
Câu hỏi:
– Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước là 1,2m và 2m.
– Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không?

Bài 8 trang 118 sgk toán lớp 8 tập 1
Đo cạnh (đơn vị mm) rồi tính diện tích tam giác vuông dưới đây (h.122):

Lời giải:
Đo hai cạnh góc vuông, ta được AB= 30mm, AC= 25mm.Áp dụng công thức tính diện tích tam giác vuông, ta được:

Bài 9 trang 119 sgk toán lớp 8 tập 1

Bài 10 trang 119 sgk toán lớp 8 tập 1
Câu hỏi:Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai góc vuông với diện tích hình vuông dựng trên cạnh huyền.

Bài 12 trang 119 sgk toán lớp 8 tập 1
Câu hỏi:Tính diện tích các hình dưới đây (h.124)( mỗi ô vuông là 1 đơn vị diện tích)
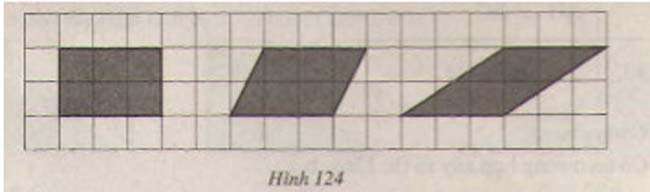
Lời giải:Diện tích hình a là 6 ô vuôngDiện tích hình b ∆ADH = ∆ BCI nên diện tích hình b sẽ bằng diện tích hình a (ABIH).Vậy diện tích hình b là 6 ô vuôngDiện tích hình c: ∆ KLN = ∆ NMO nên diện tích hình c sẽ bằng diện tích hình a (KMCB).Vậy diện tích hình c là 6 ô vuông
Bài 13 trang 119 sgk toán lớp 8 tập 1


Bài 14 trang 119 sgk toán lớp 8 tập 1

Bài 15 trang 119 sgk toán lớp 8 tập 1
Câu hỏi: Vẽ hình chữ nhật ABCD có AB = 5cm, BC = 3cm.a) Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD. Vẽ được mấy hình như vậy.b) Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật ABCD. Vẽ được mấy hình vuông như vậy? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.




Bài 1: Tính chu vi và diện tích của hình chữ nhật có chiều rộng bằng 20cm và chiều dài bằng 25cm?
Lời giải:
Chu vi của hình chữ nhật là:
(20 + 25) x 2 = 90 (cm)
Diện tích của hình chữ nhật là:
20 x 25 = 500 (cm2)
Đáp số: 90cm và 500cm2
Bài 2: Tính chu vi và diện tích của hình chữ nhật có chiều rộng bằng 15cm và nửa chu vi bằng 40cm?
Lời giải:
Chu vi của hình chữ nhật là:
40 x 2 = 80 (cm)
Chiều dài của hình chữ nhật là:
40 – 15 = 25 (cm)
Diện tích của hình chữ nhật là:
15 x 25 = 375 (cm2)
Đáp số: 80cm và 375cm2
Bài 3: Một miếng bìa hình chữ nhật có chu vi 96 cm, nếu giảm chiều dài 13 cm và giảm chiều rộng 5 cm thì được một hình vuông. Hỏi miếng bìa hình chữ nhật đó có diện tích bằng bao nhiêu?
Lời giải:
Miếng bìa hình chữ nhật có chiều dài hơn chiều rộng là:
13 – 5 = 8 (cm)
Nửa chu vi hình chữ nhật:
96 : 2 = 48 (cm)
Chiều rộng hình chữ nhật là:
(48 – 8) : 2 = 20 (cm)
Chiều dài hình chữ nhật là:
20 + 8 = 28 (cm)
Diện tích miếng bìa hình chữ nhật là:
28 x 20 = 560 (cm2)
Đáp số: 560 (cm2)
Bài 4: Tìm diện tích của một hình chữ nhật có chiều rộng 26 cm và có chu vi gấp 3 lần chiều dài?
Lời giải:
Ta có:
Chu vi = chiều dài x 3 = chiều dài x 2 + chiều dài.
Lại có:
Chu vi = chiều dài x 2 + chiều rộng x 2
Vậy: Chiều dài = chiều rộng x 2.
Chiều dài hình chữ nhật là:
26 x 2 = 52 (cm)
Diện tích hình chữ nhật là:
52 x 26 = 1352 (cm2)
Đáp số: 1352 (cm2)
Bài 5: Một miếng đất hình chữ nhật có chiều dài 64 m, chiều rộng 34 m. Người ta giảm chiều dài và tăng chiều rộng để miếng đất là hình vuông, biết phần diện tích giảm theo chiều dài là 272. Tìm phần diện tích tăng thêm theo chiều rộng.
Lời giải:
Số đo bị giảm của chiều dài miếng đất là:
272 : 34 = 8 (m)
Cạnh của miếng đất hình vuông là:
64 – 8 = 56 (m)
Chiều rộng miếng đất được tăng thêm số mét là:
56 – 34 = 22 (m)
Diện tích phần tăng theo chiều rộng miếng đất là:
56 x 22 = 1232 (m2)
Đáp số: 1232 (m2)
Cách tính chiều dài hình chữ nhật khi biết diện tích và chu vi hình chữ nhật
Cho ví dụ
Ví dụ: Cho một hình chữ nhật ABCD có tổng diện tích là 360m2 và chu vi là 98m. Hỏi chiều dài của hình chữ nhật này bằng bao nhiêu?

Cách giải: Cách này áp dụng mối tương quan giữa hai công thức tính diện tích hình chữ nhật và chu vi hình chữ nhật.
Ta có chu vi hình chữ nhật ABCD = (a + b) x 2 = (dài + rộng) x 2 = 98m
Suy ra tổng chiều dài và chiều rộng của hình chữ nhật ABCD = 98/2 = 49m
Tiếp tục sử dụng phương pháp lọc dãy số và loại trừ, ta có các cặp số chiều dài và chiều rộng sau có thể áp dụng để tính diện tích hình chữ nhật ABCD 360m2. Công thức tính diện tích hình chữ nhật bằng chiều dài nhân chiều rộng.
Diện tích 360m2 = 1 x 360 = 2 x 180 = 3 x 120 = 4 x 90 = 5 x 72 = 6 x 60, 8 x 45 = 9 x 40 = 10 x 36 = 12 x 20 = 15 x 16.
Như vậy từ công thức tính diện tích hình chữ nhật, bạn có thể quy ra tổng chiều dài và chiều rộng hình chữ nhật khi cộng lại phù hợp nhất với cặp số 9 và 40. Suy ra chiều dài của hình chữ nhật bằng 40m.
🔢 GIA SƯ TOÁN
Bài tập áp dụng
Bài tập 1:
Cho mảnh đất hình chữ nhật có diện tích 180 m2, chu vi 58 mét. Hãy tính chiều dài và chiều rộng mảnh đất đó?
Bài giải
Cách 1:
Ta có tổng của chiều rộng và chiều dài là: (58 : 2) = 29 (m)(1)
Ta phân tích diện tích HCN thành tích của số đo chiều rộng và chiều dài được như sau:
180 = 1 x 180 = 2 x 90 = 3 x 60 = 4 x 45 = 5 x 36 = 6 x 30 = 9 x 20 = 10 x 18 = 12 x 15 (2).
Dùng phương pháp đối chiếu, từ (1) ta thấy tổng số đo của chiều rộng và chiều dài là 29 m, đem đối chiếu với kết quả cặp số đo chiều rộng và chiều dài ở (2) ta thấy cặp số 9 và 20 thỏa mãn yêu cầu.
Như vậy chiều rộng là 9 m; chiều dài là 20 m.
Cách 2:
Gọi số đo chiều rộng là a; số đo chiều dài là b (a > 0; b > 0; a < b)
Theo đề bài ta có: a + b = 58 : 2 = 29 (m)(1) suy ra 0 < a < 15; 14 < b < 29.
a x b = 180 (m2) (2) suy ra a hoặc b phải chia hết cho 9.
Xét TH1: a chia hết cho 9. Vì a chia hết cho 9 và 0 < a < 15 nên a = 9.
a = 9 thì b = 29 – 9 = 20 mà 9 x 20 = 180 (thỏa mãn (2)) nên TH a = 9; b = 20
Xét TH2: b chia hết cho 9; 14 < b < 29 nên b = 18 hoặc b = 27.
– Nếu b = 18 thì a = 11 mà 11 x 18 = 198 (không thỏa mãn (2)) nên TH này ta loại.
– Nếu b = 27 thì a = 2 mà 2 x 27 = 54 (không thỏa mãn (2)) nên TH này ta cũng loại.
Vậy chiều rộng HCN là 9 m và chiều dài HCN là 20 m.
* Lưu ý: Đây là bài toán liên quan đến chu vi và diện tích hình chữ nhật. Dù vậy nó không đơn giản chỉ là bài toán tính chu vi và diện tích HCN mà cần dựa vào chu vi, diện tích của HCN để tìm ra chiều rộng và chiều dài của hình. Do đó, đòi hỏi học sinh phải nắm rõ bản chất của chu vi và diện tích HCN. Từ đó lập luận, lựa chọn TH thỏa mãn yêu cầu của bài toán.
Bài tập 2:
Cho 1 miếng bìa HCN có chu vi 150 cm. Bạn Thành lần lượt cắt dọc theo chiều rộng được 5 hình vuông và thừa ra một hình chữ nhật nhỏ hơn hình vuông đó. Hãy tính chiều dài hình chữ nhật ban đầu biết rằng số đo cạnh của các hình theo cm đều là số tự nhiên.
Bài giải
Ta có:
– Nửa chu vi miếng bìa là: 150 : 2 = 75 (cm)
– Theo như đề bài chiều dài miếng bìa bị cắt thành 5 phần với mỗi phần bằng chiều rộng, còn dư một phần nhỏ hơn chiều rộng. Giả sử coi chiều rộng là a (a > 0) và phần dư là b (b > 0) thì nửa chu vi sẽ là:
a + a x 5 + b = a x 6 + b = 75 (cm)
mặt khác: 75 = 12 x 6 + 3 = 11 x 6 + 9 (3 < 12; 9 < 11). Vậy 2 TH này đều thỏa mãn điều kiện của bài toán.
– Nếu chiều rộng là 12 cm thì chiều dài là: 75 – 12 = 63 (cm)
– Nếu chiều rộng là 11 cm thì chiều dài là: 75 – 11 = 64 (cm)
Như vậy có thể kết luận chiều dài HCN là 63 cm hoặc 64 cm
Bài tập 3:
1 mảnh vườn hình chữ nhật có chiều dài gấp 5 lần chiều rộng và diện tích là 720m2. Hãy tìm chu vi mảnh vườn đó biết rằng mỗi cạnh của mảnh vườn đều là những số tự nhiện.
Bài giải:
Chiều dài gấp 5 lần chiều rộng nên có thể chia mảnh vườn thành 5 mảnh hình vuông có cạnh bằng chiều rộng.
Ta có diện tích mỗi mảnh hình vuông là: 720 : 5 = 144 (m2)
Mà : 144 = 12 x 12 suy ra cạnh hình vuông hay chiều rộng của mảnh vườn là 12 m.
Từ đó tính được:
– Chiều dài của mảnh vườn là: 12 x 5 = 60 (m)
– Chu vi của mảnh vườn là: (60 + 12) x 2 = 144 (m)
Bài luyện tập tính chu vi, diện tích hình chữ nhật
Bài 1: Một hình chữ nhật có chu vi 72 cm. Nếu giảm chiều rộng đi 6cm và giữ nguyên chiều dài thì diện tích giảm đi 120 cm2.
Tính chiều dài và chiều rộng hình chữ nhật đó.
Bài 2: Một mảnh đất hình chữ nhật có chiều dài 14 m. Nếu chiều rộng tăng 2 m, chiều dài giảm 3m thì mảnh đất đó trở thành hình vuông. Tính chu vi mảnh đất đó.
Bài 3: Một mảnh đất hình chữ nhật có chiều dài 12 m, biết rằng 3 lần chiều rộng thì bằng 2 lần chiều dài. Tính chu vi mảnh đất đó.
Bài 4: Nếu bớt một cạnh hình vuông đi 4 cm thì được hình chữ nhật có diện tích kém diện tích hình vuông 60 cm2. Tính chu vi hình vuông đó.
Bài 5: Một hình vuông có chu vi là 24 cm. Một hình chữ nhật có chiều rộng bằng cạnh của hình vuông và biết 3 lần cạnh hình vuông thì bằng 2 lần chiều dài hình chữ nhật. Tính diện tích mỗi hình đó.
Bài 6: Biết chu vi một hình chữ nhật gấp 6 lần chiều rộng. Hỏi chiều dài hình chữ nhật đó gấp mấy lần chiều rộng?
Bài 7: Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Tính chu vi hình chữ nhật đó, biết diện tích của nó là 32 cm2.
Bài 8: Một hình chữ nhật có chu vi là 64 m, chiều rộng bằng 1/3 chiều dài. Tính diện tích hình chữ nhật đó.
Bài 9: Một hình chữ nhật và một hình vuông có chu vi bằng nhau và bằng 36cm. Chiều rộng hình chữ nhật bằng 1/2 chiều dài. Hỏi diện tích hình vuông hơn diện tích hình chữ nhật bao nhiên xăng-ti-mét vuông?
Bài 10: Một hình vuông được chia thành 2 hình chữ nhật. Tính chu vi hình vuông, biết rằng tổng chu vi 2 hình chữ nhật là 6420 cm.
Bài 11: Một hình chữ nhật có chu vi gấp đôi chu vi hình vuông cạnh 415m. Tính chiều dài và chiều rộng hình chữ nhật đó. Biết chiều dài gấp 4 lần chiều rộng.
Bài 12: Một hình chữ nhật có chu vi bằng 5 lần chiều rộng. Biết chiều dài bằng 60 cm. Tính chu vi hình chữ nhật.
Bài 13: Một tấm bìa hình chữ nhật có hai lần chiều rộng kém chiều dài 6cm, nhưng chiều dài lại kém năm lần chiều rộng là 3cm. Tính diện tích tấm bìa hình chữ nhật đó.
Bài 14: Một hình chữ nhật có chiều rộng 4cm, chiều rộng kém chiều dài 8 m.
a. Tính diện tích hình chữ nhật.
b. Hãy chia hình chữ nhật trên thành 2 hình: một hình vuông có cạnh bằng chiều rộng hình chữ nhật ban đầu và một hình chữ nhật. Tính tổng chu vi của hình vuông và hình chữ nhật mới đó.
Bài 15: Một hình chữ nhật có chu vi 70 cm, được chia thành hai phần bởi một đoạn thẳng song song với chiều rộng sao cho phần thứ nhất là một hình vuông, phần thứ hai là hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Tìm diện tích hình chữ nhật ban đầu?
Từ khóa » Chu Vi đáy Là Gì
-
Chu Vi Là Gì – Công Thức Tính Chu Vi Những Hình Cơ Bản Trong Toán Học
-
Chu Vi Là Gì? Cách Tính Chu Vi Các Hình Trong Toán Học
-
Công Thức Tính Chu Vi Hình Chữ Nhật, Diện Tích Hình Chữ Nhật
-
Chu Vi – Wikipedia Tiếng Việt
-
Công Thức Tính Diện Tích Chu Vi Các Hình Cơ Bản. - Tài Liệu Text - 123doc
-
CHU VI LÀ GÌ ? CÁCH TÍNH CHU VI - "Đơn Giản Thế Mà Mình Không ...
-
Chu Vi Kí Hiệu Là Gì - Công Thức Tính Diện Tích Chu Vi Các Hình ...
-
Cho Hình Trụ Có Chu Vi đáy Là (10pi ) Và Chiều Cao (h = 11 ) .
-
Chu Vi đáy Của Một Cái Hộp Hình Lập Phương Là 96 Cm . Tính Diện Tích ...
-
1.Cách Tính Nửa Chu Vi đáy Hình Lăng Trụ đứng 2. Cách ... - MTrend
-
Công Thức Tính Chu Vi Diện Tích Và Thể Tích Của Hình Trụ Rõ Ràng Nhất
-
Công Thức Tính Chu Vi Mặt đáy Và Diện Tích Mặt đáy Của Hình Hộp Chữ ...
-
Hướng Dẫn Cách Tính Diện Tích Xung Quanh Hình Trụ Chuẩn Xác 100%
-
Cách Tính Thể Tích Hình Trụ - Từ Điển Toán Học