Cách Tính Diện Tích Toàn Phần Hình Trụ - Thủ Thuật Phần Mềm
Có thể bạn quan tâm
Nếu các bạn đang tìm kiếm cách tính diện tích toàn phần hình trụ để làm các bài tập yêu cầu tính diện tích toàn phần hình trụ. Vậy mời các bạn cùng tham khảo công thức và cách tính diện tích toàn phần hình trụ mà bài viết chia sẻ dưới đây.
Hình trụ tròn là một hình trụ có hai đáy là hai đường tròn bằng nhau, diện tích toàn phần hình trụ bằng diện tích xung quanh hình trụ cộng với diện tích của 2 đáy.
Giả sử hình trụ có chiều cao là h và bán kính đường tròn đáy là r giống như hình vẽ.
Công thức tính diện tích xung quanh hình trụ
\[{S_{xq}} = 2\pi rh\]
Công thức tính diện tích 2 đường tròn đáy
\[{S_{2đ}} = 2\pi {r^2}\left( {{S_đ} = \pi {r^2}} \right)\]
=> Công thức tính diện tích toàn phần hình trụ:
\[{S_{tp}} = 2\pi {r^2} + 2\pi rh = 2\pi r\left( {r + h} \right)\]
Trong đó:
- \({S_{xq}}\) là diện tích xung quanh hình trụ.
- \({S_{2đ}}\) là diện tích 2 đường tròn đáy hình trụ, \({S_{đ}}\) là diện tích đường tròn đáy.
- \({S_{tp}}\) là diện tích toàn phần hình trụ.
- \(\pi \) là hằng số \(\pi \) = 3.14159265359
- r là bán kính đường tròn đáy.
- h là chiều cao hình trụ.
Cách tính diện tích toàn phần hình trụ
Để tính diện tích toàn phần hình trụ các bạn có thể tính lần lượt diện tích đường tròn 2 đáy và diện tích xung quanh hình trụ sau đó tính tổng hai diện tích sẽ được diện tích toàn phần:
1. Đầu tiên các bạn cần tính diện tích đường tròn đáy hình trụ sử dụng công thức tính \({S_{đ}}\)
\[{{S_đ} = \pi {r^2}}\]
Nếu biết bán kính r thì các bạn chỉ cần áp dụng luôn công thức, nếu bán kính r chưa biết thì các bạn cần dựa vào dữ liệu để tìm r. Sau đó tính diện tích đường tròn đáy hình trụ.
2. Tiếp theo các bạn cần tính diện tích xung quanh hình trụ
Công thức tính diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\)
Thường thì chiều cao sẽ được cho sẵn, các bạn biết bán kính r ở bước 1, vì vậy các bạn sẽ dễ dàng tính được diện tích xung quanh hình trụ.
3. Cuối cùng chỉ cần áp dụng công thức để tính diện tích toàn phần hình trụ
\[{S_{tp}} = 2.{S_đ} + {S_{xq}}\]
Hoặc các bạn có thể tìm bán kính r và chiều cao h từ yêu cầu của đề bài sau đó các bạn áp dụng trực tiếp công thức tính diện tích toàn phần hình trụ:
\[{S_{tp}} = 2\pi {r^2} + 2\pi rh = 2\pi r\left( {r + h} \right)\]
Ví dụ
Ví dụ 1: Tính diện tích toàn phần của hình trụ, có độ dài đường tròn đáy là 10cm, khoảng cách giữa 2 đáy là 6cm.
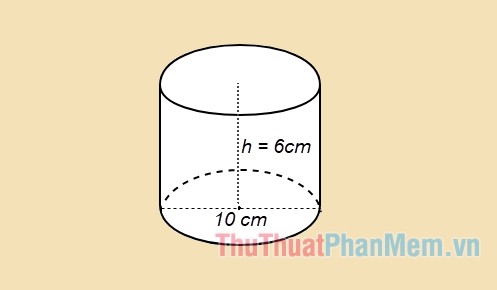
Giải
Theo đề bài ta có: h = 6cm; 2r = 10cm => r = 5cm.
Áp dụng công thức tính diện tích toàn phần hình trụ:
\[{S_{tp}} = 2\pi r\left( {r + h} \right) = 2\pi .5\left( {5 + 6} \right) = 110\pi \left( {c{m^2}} \right)\]
=> Vậy diện tích toàn phần của hình trụ là \(110\pi \left( {c{m^2}} \right)\)
Ví dụ 2: Tính diện tích toàn phần của hình trụ có chiều cao là 7cm và diện tích xung quanh bằng 310 \(\left( {c{m^2}} \right)\)
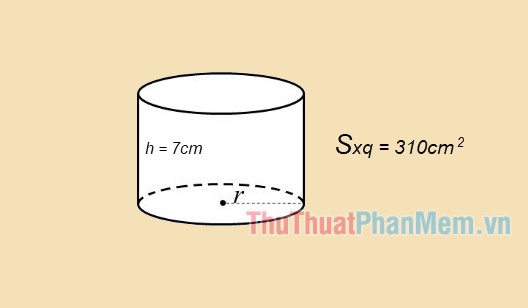
Giải
Theo đề bài ta có: h = 7; \({S_{xq}} = 310\)
Áp dụng công thức tính diện tích xung quanh \({S_{xq}} = 2\pi rh\)
=> \(r = \frac{{{S_{xq}}}}{{2\pi rh}} = \frac{{310}}{{2\pi .7}} \approx 7cm\)
Vậy \({{S_đ} = \pi {r^2} = \pi {{.7}^2} = 49\pi \approx 154c{m^2}}\)
=> Diện tích toàn phần của hình trụ: \({S_{tp}} = 2.{S_đ} + {S_{xq}} = 2.154 + 310 = 618c{m^2}\)
Trên đây bài viết đã chia sẻ đến các bạn công thức, ví dụ cụ thể về cách tính diện tích toàn phần hình trụ. Hi vọng bài viết sẽ giúp các bạn hiểu rõ hơn về cách tính diện tích toàn phần hình trụ để áp dụng tính toán cho các bài toán cụ thể. Chúc các bạn thành công!
Từ khóa » Ct Tính Diện Tích Hình Trụ Tròn
-
Công Thức Tính Thể Tích Hình Trụ, Diện Tích Xung Quanh Và Toàn Phần ...
-
Công Thức Tính Thể Tích Hình Trụ, Diện Tích Xung Quanh Hình Trụ Và Toà
-
Công Thức Tính Diện Tích Hình Trụ, Ví Dụ Và Lời Giải Chi Tiết - Thủ Thuật
-
Công Thức Tính Diện Tích Xung Quanh Hình Trụ - THPT Sóc Trăng
-
Diện Tích Xung Quanh Hình Trụ, Diện Tích Toàn Phần Hình Trụ
-
Diện Tích Toàn Phần Hình Trụ Tròn Xoay Là Gì ? Cách Tính Kèm Ví Dụ ...
-
Công Thức Tính Diện Tích Hình Trụ Tròn, Thể Tích ... - DINHNGHIA.VN
-
Công Thức Tính Diện Tích, Thể Tích Hình Trụ Như Thế Nào?
-
Công Thức Tính Diện Tích Xung Quanh Hình Trụ Và Toàn Phần Hình Trụ Tròn
-
Công Thức Tính Diện Tích Hình Trụ, Thể Tích Hình Trụ
-
Hướng Dẫn Cách Tính Diện Tích Xung Quanh Hình Trụ Chuẩn Xác 100%
-
Công Thức Tính Diện Tích Hình Trụ, Cách Để Tính Thể Tích Hình Trụ
-
Cách để Tính Diện Tích Toàn Phần Của Hình Trụ - WikiHow