CÁCH TÍNH LIM (giới Hạn) BẰNG CASIO FX 570 ES

Trang chủ » Cách Bấm Casio Tính Lim » CÁCH TÍNH LIM (giới Hạn) BẰNG CASIO FX 570 ES

Có thể bạn quan tâm

CÁCH TÍNH LIM (giới hạn) BẰNG CASIO FX 570 ES

CÁCH TÍNH LIM (giới hạn) BẰNG CASIO FX 570 ES

I) tính lim x -> + 1: nhập biểu thức cần tính lim, ví dụ:2: Ấn CALC3: Nhập một số thật lớn (vì x tiến s về +), ví dụ 9 x10 9, 9999999,98989898,...

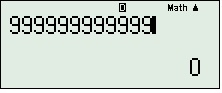
4:Ấn =, có kết quả gần đúng hoặc đúng

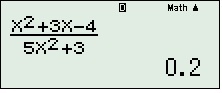
5: lấy kết quả "đẹp" (ở đây là 0.2), ví dụ: nếu nó ra 0,99999999999 thì bạn lấy kết quả là 1, 1,333334-->1,333333-->6: nếu kết quả là số rất lớn (985764765, 36748968,1.2534x10^28,...) hoặc rất bé(-846232156,..), đừng sợ, đó là +vô cùng (và - vô cùng) đó!II) Tính lim x-> - tương tự bên trên, thêm dấu trừ ví dụ: -9x10 9, -999999999, -88888888,...III) Tínhví dụ:1, nhập biểu thức 2, Ấn CALC3, bấm 1+ (vì tiến về 1+)4, nhập [1] [x10x] [-] [9] hoặc một số thật nhỏ, ví dụ: 0,000000001,...

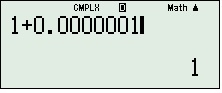
5, Ấn =, có kết quả gần đúng hoặc đúng

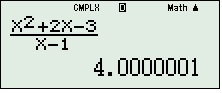
6, lấy kết quả "đẹp" (ở đây là bằng 4), ví dụ: nếu nó ra 0,99999999999 thì bạn lấy kết quả là 1, 1,333334-->1,333333-->

  • nếu kết quả là số rất lớn (985764765, 36748968, 1.2534x10^28 ...) hoặc rất bé(-846232156,..), đừng sợ, đó là + (và -) đó!
  • Nếu kết quả có dạng , ví dụ: 5.12368547251.10^-25, nghĩa là 0,000...00512... (gần về 0), kết quả là 0

IV) Tính tương tự, đổi 1+ thành 1-*) VÍ DỤ ÁP DỤNG:

  • tính , ta bấm ,bấm CALC, bấm 2+ (vì đề chỉ cho tiến về 2 nên ta tạm cho nó về 2+ trước), bấm [1] [x10x] [-] [9] [=] (1.10^-9= 0.000000001 là một số rất nhỏ), máy hiện kết quả là 1.49998, ta làm tròn là 1.5, dạng phân số là 3/2
  • Tính , ta bấm , bấm CALC, bấm [9] [x10x] [9] [=] (9.10^9= 9000000000, số rất lớn), máy hiện kết quả 1

CÁCH NHÂN, CHIA ĐA THỨC CHỈ BẰNG MÁY TÍNH (nhanh hơn cách dùng hoocne)

Phương pháp này mình nghĩ ra năm lớp 10 và thấy khá hữu ích trong áp dụng giải đề thi đại học, mình muốn chia sẻ với mọi người và hy vọng giúp đỡ được các bạn phần nào trong đề thi đại học :) Ở Việt Nam, đây là trang web đầu tiên đăng tải phương pháp bấm máy này. Bạn nào nếu có ý tưởng phát triển thêm này thì cứ liên hệ mình qua Face nha, có gì mình cùng hợp tác nghiên cứuNếu các bạn đã xem một số bài viết được viết lại tương tự ở một trang nào khác thì cũng nên đọc bài viết của mình để được cập nhật chính xác và đầy đủ nhất về phương pháp bấm máy sau đây. (Ví dụ như vì sao nên dùng 1000 thay vì 100 trong quá trình tính toán, vân vân và vân vân...) Mời các bạn đến với bài viết:Hehe! Có bao giờ bạn nghĩ rằng bạn có thể nhân những đa thức loằng ngoằng phức tạp bằng cách chỉ sử dụng máy tính không? Ví dụ: (x+1)(x+2)+(3x2+x+6)(x+7), bạn giải ra kết quả là 3x3+23x2+16x+44Bây giờ tôi sẽ giải bài này chỉ bằng cách bấm máy tính do tôi nghĩ ra!Bạn bấm 1000 [=] (Ans+1)(Ans+2)+(3Ans2+Ans+6)(Ans+7) [=]Máy hiện 3023016044, bạn tách chúng thành từng cụm ba chữ số 3,023,016,044 (nhớ là từ tách bên phải sang nghe), và đó chính là các hệ số cần tìm 3,23,16,44. Ta viết 3x3+23x2+16x+44Thế là xong! Thử lại bằng cách bấm qua trái, bấm thêm –(3Ans3+23Ans2+16Ans+44)=, máy báo bằng 0, phép tính mình đúngXin giải thích một chút về quy trình bấm phím: bạn bấm 1000 [=] cho mọi bài toán,khi nhập phép tính thay x bằng AnsVí dụ 2: (5x-3)(x2+6x-7)+10x-21Bạn vẫn bấm như trên: 1000 [=] (5Ans-3)(Ans2+6Ans-7)+10Ans-21 [=]Máy hiện 5026957000, bạn vẫn tách như trên 5,026,957,000Từ phải sang, Nhóm 000, không có vấn đề gì, lấy hệ số là 0Lần này phải cẩn thận hơn! Ở nhóm 957 ta hiểu là -43 (vì 1000-957=-43) chứ không phải 957! Vì sao ư? Đơn giản là vì 957 là số quá lớn không thể là hệ số của phép nhân này được và ta phải lấy 1000 trừ cho nhóm đóDấu hiệu cần chú ý tiếp theo là nhóm 026, nhóm này đứng sau nó là nhóm 957 (nhóm có hệ số âm), vậy ta lấy 26+1=27, hiểu đơn giản đằng sau nhóm có hệ số âm thì phải nhớ 1 (như kiểu học cấp 1 ý hihi)Tóm lại, các hệ số cần tìm 5,27,-43,0 biểu thức cần tìm là 5x3+27x2-43x. Ta thử lại bằng cách qua trái, bấm thêm -(5Ans3+27Ans2-43Ans)= máy báo bằng 0 nghĩa là đúngVí dụ 3: (x2-3x+7)(x+2) bạn bấm 1000 [=](Ans2-3Ans+7)(Ans+2) [=]Máy hiện 999001014 tách thành 0,999,001,014 các hệ số lần lượt là 1,-1,1,14. Kết quả 14x3+x2-x+1. Ta thử lại bằng cách bấm qua trái, bấm thêm -(14Ans3+Ans2-Ans+1)= máy báo bằng không nghĩa là đúngVí dụ 4: (x2-3x-7)(x+2) bạn bấm 1000 [=](Ans2-3Ans-7)(Ans+2)[=], máy hiện 998986986, tách thành 0,998,986,986. Bài này ta phân tích từ phải qua như sau 986 thành -14, tiếp theo 986 nhớ 1 là 987 rồi thành -13, tiếp theo 998 nhớ 1 là 999 rồi thành -1các hệ số ta suy ra 1,-1,-13,-14 ta có kết quả x3-x2-13x-14. Ta thử lại bằng cách qua trái, bấm -(Ans3-Ans2-13Ans-14)= máy báo bằng 0 nghĩa là đúngVí dụ 5: (x+5)(x+3)(x-7)-(4x2-3x+7)(x-1) làm tương tự, máy hiện -2992051098, ta có các hệ số 3,-8,51,98. Ta coi dấu trừ ở dãy số hiện ra là dấu trừ cho toàn bộ biểu thức. Vậy kết quả là -(3x3-8x2+51x+98)= -3x3+8x2-51x-98. Ta thử lại bằng cách qua trái, bấm -(-3Ans3+8Ans2-51Ans-98)= máy báo bằng 0 nghĩa là đúngVí dụ 6: (x2+3x+2)(5-3x)-(x+2)(x-1)-(2x+3)(x-1)Đến bài này mình xin trình bày luôn cách dùng nháp kết hợp nhẩm sao cho có hiệu quả, giúp các bạn tự tin hơn trong việc vận dụng làm toánBạn làm tương tự như các bài trên, máy hiện -3006992985. Chuẩn bị 1 tờ giấy nháp và viết vào nháp các hệ số từ phải sang lần lượt như saulần 1 -15lần 2 -7 -15lần 3 7 -7 -15lần 4 3 7 -7 -15lần 5 -3 -7 +7 +15 (vì có dấu trừ ở đầu)thử lại bằng cách qua trái -(-3Ans3-7Ans2+7Ans+15)= máy báo bằng 0 nghĩa là kết quả đúngGhi vào bài làm chính thức kết quả -3x3-7x2+7x+15Ví dụ 7,8,9: (tự luyện)(-5x2+3x-2)(x+1)+5x-7 = -5x3-2x2+6x-9(2x2+3x-7)(x-3)+(2-x)(x+1)(x-3) = x3+x2-17x+15x3+5x-7+(x2+3)(x-4) = 2x3-4x2+8x-19Ví dụ chia đa thức:Thông thường chia đa thức người ta thường dùng cách chia được dùng năm lớp 8 hoặc nếu chia không dư ta có thể dùng phương pháp chia hoocne (horner). Nhưng với phương pháp này ta có thể dùng để chia đa thức ko dư mà không cần dùng đến hoocne (horner). Nếu bạn hiểu cách nhân đa thức rồi thì chỉ cần thay nhân bằng chia là đượcbài toán (2x3-3x2-16x+21)/(x-3) ta bấm tương tự như nhân đa thức ra kết quả 2002993, vậy kết quả là 2x2+3x-7Cách này dù không chia có dư được nhưng lại rất có giá trị trong việc nhẩm nghiệm phương trình bậc 3 hoặc bậc 4Ví dụ: x^3+4x^2-3x-2=0Bấm máy ra một nghiệm chẳn x=1 và hai nghiệm lẻchia (x^3+4x^2-3x-2) cho (x-1) ra x^2+5x+2giải tiếp phương trình trên x^2+5x+2=0 ra hai nghiệm lẻ còn lại là (-5+ căn 17)/2 và (-5-căn 17)/2xong!Đối với những bạn dùng máy VINACAL fx570es plus ta có thể thực hiện phép chia có dư với tính năng Q...rCác bạn bấm 1000= Shift VINACAL 1 sau đó nhập tử số Shift ) sau đó nhập mẫu số. Kết quả sẽ cho ra Q= kết quả R= số dưBản chất: Hy vọng qua những ví dụ cụ thể trên các bạn có thể cơ bản nắm được bản chất của phương pháp này. Bản chất chỉ là thế giá trị 1000 vào tất cả các giá trị x để tính toán thôi. Mặc dù rất đơn giản nhưng rất có ích không phải ai cũng biết.Ưu điểm của phương pháp: nhanh, ra kết quả có độ chính xác cao (hơn giải tay rất nhiều)Hầu hết đề thi bậc phổ thông đều không có hệ số quá phức tạp nên áp dụng cách này rất hữu hiệu!Lưu ý: Mình có một yêu cầu thế này, trong mọi bài toán bước thử lại là không thể bỏ qua. Bước thử lại gần như là linh hồn của phương pháp này. Nó không mất của bạn quá vài giây, nhưng nếu bạn ko làm thì phương pháp này trở thành con dao hai lưỡi giết chết bạn. Nếu bạn thử lại ở mọi bài toán, bạn sẽ không còn hoài nghi gì về kết quả hay phương pháp mình làm đúng hay sai nữa. Nhờ việc thử lại những bước trước bạn có thể tự tin nhẩm mà không sợ sau này kết quả sai. Theo kinh nghiệm của mình, khi bạn đã thuần thục phương pháp này, thời gian bạn hoàn thành một phép tính bao gồm cả thử lại chỉ 5 giây, thậm chí với những bài toán đơn giản áp dụng phương pháp này vẫn rất nhanh (cái này gọi là phụ thuộc máy tính đó, hehe). Phương pháp này mình nghĩ ra từ hè 11 lên 12, mình có cả năm 12 để rèn luyện để tìm ra ưu nhược điểm của phương pháp, và mình kết luận bước thử lại là quan trọng nhất. Nó đem lại một ưu điểm mà phương pháp giải tay không bao giờ đem lại được, đó là tính chính xác. Nhiều khi vì sự chính xác này đến cả những bài đơn giản như (x+1)(x+2) cũng có thể bấm máy, vì biết đâu nếu mình giải tay thì sai bước nào đó thì sao.Ngoài ra, bước nhập biểu thức ban đầu, sau khi nhập xong bạn nên dùng con trỏ rà lại để đảm bảo mình nhập đúng. Nếu bạn làm đúng thì không sợ gì kết quả sai nữa Thêm một lưu ý nữa là nhớ mở ngoặc thì phải đóng ngoặc. Việc mở ngoặc đóng ngoặc bậy bạ cũng là một nguyên nhân gây sai kết quả. Nhưng thường sau khi thử lại bạn sẽ nhìn ra điểm sai của mình để sửa nên ko saoTrong một số trường hợp bạn thử lại kết quả vẫn sai thì bạn nên chuyển sang giải tay cho kịp giờ. Còn nếu lúc rảnh rỗi thì bạn cố gắng kiểm tra xem mình sai ở bước nào, từ đó rút được kinh nghiệm.Trong trường hợp hệ số là phân số thì phương pháp này không đúng, trường hợp này ta nên chuyển về số nguyên để tính toán cho thuận tiện Phương pháp bấm máy này mình đã vận dụng vào kì thi đại học rất thành công. Ở môn toán, gần như ko có bài nào là mình không áp dụng, nó đã hạn chế sai sót của mình rất nhiều. Mình muốn khẳng định rằng phương pháp này cực kì có ý nghĩa trong đề thi đại học.Tại sao không phải 100 mà là 1000?Cài này nhiều bạn thắc mắc. Dĩ nhiên là thế 1000 hay 100 đều giống nhau, chỉ cần thay vì nhóm 3 chữ số thì chuyển sang nhóm 2 chữ số thôi. Nhưng qua quá trình nghiên cứu mình xin khẳng định là không nên dùng 100. Vì chọn 100 giúp ta làm gọn kết quả trên màn hình và có thể tính toán lên đến bậc 4 (thậm chí bậc 5) nhưng lại rất dễ sai ở các hệ số từ 25 trở lên (có lúc hệ số dưới 10 mà vẫn sai). Với 1000 thì mọi hệ số có 2 chữ số đều đảm bảo đúng (khoảng dưới 200 vẫn đúng). Qua quá trình học 12 ôn thi đại học, rất ít trường hợp tính toán bậc 4 nhưng lại rất nhiều trường hợp hệ số đạt đến 50 (rất nhiều lần là hơn 100). Lúc đó, nếu áp dụng 100 thì lúc bạn thử lại kết quả sẽ là sai và bạn phải chuyển sang 1000 mới có kết quả đúng. Mình cũng không cứng nhắc bắt các bạn chọn 1000 vì có nhiều khi sử dụng song song rất có hiệu quả. (Nhưng ít lắm)Nếu bạn nào muốn tham khảo bài viết này của mình để chia sẻ hoặc sáng tạo thêm để đăng trên các website diễn đàn khác nên liên hệ trước qua facebook của mình hoặc ghi thêm "tham khảo Trần Ngọc Ánh Phương - kinhnghiemhoctap.blogspot.com"CALC 1000: Có lẽ đến đây nhiều bạn đã cơ bản nắm được bản chất của phương pháp bấm máy này. Việc bấm 1000= chẳng qua chỉ là gán giá trị 1000 cho Ans rồi ta thực hiện phép tính, vậy nên đối với những bạn đang dùng máy tính Casio/Vinacal fx 570 ta có một cách trực quan hơn để sử dụng phương pháp này. Đó là dùng lệnh CALC rồi gán 1000 cho X.Ví dụ 1(5x+7)(2x2-3x+5)-(x-2)(x+5)(x-3)Kết quả: 9x3-x2+23x+5Ta bấm: (5X+7)(2X2-3X+5)-(X-2)(X+5)(X-3) CALC 1000 =Máy ra kết quả 8999023005, nghĩa là 9x3-x2+23x+5Ta thử lại bằng cách bấm: qua trái -(9x3-x2+23x+5) CALC 7=Nếu máy ra kết quả bằng 0 nghĩa là ta làm đúng. Vậy là xong, khoẻ re!Xin giải thích thêm, để nhập "X" ta bấm alpha ). Còn phím CALC là phím ở ngay dưới phím shiftỞ đây việc bấm CALC nhằm ra lệnh cho máy gán giá trị nào đó vào ẩn x (cái này chắc là nhiều bạn biết rồi nhỉ). Cụ thể ở đây là gán 1000 vào X. Ở bước thử lại, ta bấm CALC 7= nhằm thử thế một giá trị khác vào X. Ngoài 7 ra ta có thể thế bất cứ số nào, số 7 mình chỉ lấy ví dụ thôi, nhưng không được lấy những số như 10,100,1000,... Bạn nhớ nhé! Tốt nhất cứ theo mình CALC 7= là đượcCó nhiều bạn ở bước thử lại này "lười" bấm CALC 7= mà cứ = luôn, như vậy kết quả thử lại là với số 1000 bạn nhập lúc đầu rất dễ gây sai sót. Cái này mình bị dính rồi nên kinh nghiệm hihi.Các bạn hãy thử làm lại những bài ở trên với cách mới này đi!Mình thường sử dụng song song hai phương pháp "gán Ans" và "gán X". Qua thực thiễn mình thấy X mặc dù phải bấm hai phím alpha ) để nhập trong khi Ans chỉ một phím nhưng việc hiển thị X giúp ta dễ nhìn hơn. Tiêu chí mình đặt ra luôn là "chính xác" quan trọng nhất, vì vậy việc "gán X" giúp ta dễ nhận ra sai sót lúc nhập số liệu ban đầu.Nếu bạn nào muốn tham khảo bài viết này của mình để chia sẻ hoặc sáng tạo thêm để đăng trên các website diễn đàn khác nên liên hệ trước qua facebook của mình hoặc ghi thêm "tham khảo Trần Ngọc Ánh Phương - kinhnghiemhoctap.blogspot.com" Khai triển đa thức có chứa tham số m bằng CALC 1000 kết hợp số phức:Anh Mẫn Tiệp (Hậu Giang) sau đọc được bài viết này đã nghĩ ra phương pháp này. Thực sự nó rất có ích trong câu 1b của đề thi đại học. Các bạn cùng đến với ví dụ đầu tiên nhéVí dụ 1: 3(x-1)3-5m(x-1)2+m(x-1)+2-mKết quả là 3x3-(9+5m)x2+(11m+9)x-1-7mTa bấm như sauB1: chọn chế độ số phức MODE 2B2: Nhập 3(X-1)3-5i(X-1)2+i(X-1)+2-i CALC 1000=Ở đây ta thay m bằng i {phím ENG}, X phím Shift )B3: Máy hiện kết quả (có thể bấm thêm phím S<=>D để kết quả rõ ràng hơn)B4: Ta có dãy số đầu tiên tương ứng với các hệ số 3,-9,9,-1. Dãy thứ hai có chứa i cũng làm tương tự, ta có các hệ số -5,11,-7B5: Vậy kết quả là 3x3-9x2+9x-1+m(5x2+11x-7) = 3x3-(9+5m)x2+(11m+9)x-1-7mB6: Thử lại: qua trái, nhập -(3X3-(9+5i)X2+(11i+9)X-1-7i) CALC 7= máy báo bằng 0 nghĩa là kết quả đúngB7: Bấm MODE 1 để quay lại chế độ thông thường. Nếu bạn cứ để máy ở Mode CMPLX thì một số chức năng của máy có thể bị hạn chế đấyVí dụ 2: x2-2mx+(5x-3)(4x+m) = 21x2-12x+3mx-3m, bài này các bạn làm tương tự là được ^^B1: chọn chế độ số phức MODE 2B2: Nhập X2-2iX+(5X-3)(4X+i)B3: Máy hiện kết quảB4: Hệ số không chứa i (không chứa m): 21,-12,0Hệ số chứa i (chứa m): 3,-3B5: vậy kết quả là 21x2-12x+m(3x-3) = 21x2-12x+3mx-3mB6: Thử lại: qua trái, nhập -(21X2-12X+3iX-3i) CALC 7= máy báo bằng 0 nghĩa là kết quả đúngB7: Bấm MODE 1 để quay lại chế độ thông thườngVới phương pháp này dù chỉ áp dụng với m bậc nhất nhưng trong đề thi câu 1b thường là bậc 1 nên phương pháp này thực sự rất có hiệu quả.đang cập nhật... 90%

Nếu bạn nào muốn tham khảo bài viết này của mình để chia sẻ hoặc sáng tạo thêm để đăng trên các website diễn đàn khác nên liên hệ trước qua facebook của mình hoặc ghi thêm "tham khảo Trần Ngọc Ánh Phương - kinhnghiemhoctap.blogspot.com"

KIỂM TRA TÍNH ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ, NHẨM NGHIỆM NGUYÊN CỦA PHƯƠNG TRÌNH

a) Nhẩm nghiệm nguyên của phương trình:Trong nhiều bài toán việc đoán ra 1 nghiệm mang ý nghĩa quyết định. Những bài toán nhẩm nghiệm thường có nghiệm là số nguyên nhỏ (ví dụ như 0,1,2,3,...) bởi vậy việc sử dụng tính năng TABLE của Casio/Vinacal fx570es sẽ rất tiết kiệm thời gian và công sức cho các bạn.Chức năng TABLE có chức năng thay một loạt số vào một biểu thức rồi hiển thị cho ta kết quả. Vì vậy ta dùng tính năng này để thay dãy số -14,-13,-12,...,0,1,...15 vào phương trình cần nhẩm để xem giá trị nào là nghiệmTrong đề thi đại học khối B năm 2013 mình vừa thi có áp dụng cách này trong một ý của câu hệ phương trình, mình xin dẫn ra làm ví dụ luônTa xét phương trình sau . Để giải được bài này ta phải đoán nghiệm trước. Đầu tiên ta bấm MODE 7 để mở chức năng table, màn hình xuất hiện Ta chuyển toàn bộ phương trình về vế trái rồi nhập vào màn hình Bấm =, máy báo Nhập -14= sau đó máy báo Nhập 15= sau đó máy báo Nhập 1= sau đó máy ra kết quả Ta sẽ thấy một bảng dài gồm hai cột X và F(x). Cột X là số ta thay vào. Cột F(x) là kết quả của biểu thức mà ta nhập lúc đầu. ví dụ với X=2 thì = 6,6125Ta kéo xuống sẽ thấy tương ứng với X=0 và X=1 thì biểu thức có giá trị bằng 0. Nghĩa là x=0 và x=1 là hai nghiệm phương trình (từ đó, ta có thể nhanh chóng tìm ra hướng giải cho bài toán trên)Mình xin giải thích thêm về các bước nhập start, end, step ở trên. Start? nghĩa là máy hỏi dãy số mình định thế vào X bắt đầu bằng số mấy. End? nghĩa là máy hỏi dãy số mình định thế vào X kết thúc bằng số mấy. Step? nghĩa là máy hỏi các số cách nhau bao nhiêu. Ở đây, mình nhập là dãy số chạy từ -14 đến 15 cách nhau 1 đơn vị.Làm xong bạn bấm MODE 1 để quay lại chế độ ban đầuCác bạn làm tương tự với phương trình sau (cũng lấy từ đề khối B-2013)Chọn MODE 7 (nếu đang ở sẵn chế độ TABLE thì khỏi bấm, ON thôi là được)Nhập = -14= 15= 1= máy hiện ra kết quả. Ta kéo xuống thấy, khi X=0 thì F(x) cũng bằng 0. Vậy x=0 là nghiệm phương trình Trên đây chỉ trình bày cách nhẩm nghiệm, còn cụ thể bài hệ phương trình khối B-2013 giải như thế nào thì bạn bấm vào link sau đây http://i.imgur.com/3ZLA7H8.jpg?1?3572Các bạn thử áp dụng phương pháp nhẩm nghiệm với phương trình sau . Ta thấy phương trình này có hai nghiệm 0,1 từ đó ta có thể nghĩ đến phương pháp đạo hàm hai lần để chứng minh bài này không quá 2 nghiệm, từ đó giải được bài toán. b) KIỂM TRA TÍNH ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ:Đang cập nhật... xin các bạn like fanpage bên dưới để mình tiện thông báo khi cập nhật xongTrong quá trình sử dụng chức năng TABLE mình nghĩ ra một cách khá hay để tận dụng nó vào việc kiểm tra tính đồng biến, nghịch biến. Trong nhiều bài toán phương trình hệ phương trình, ta băn khoăn không biết là hàm số đó có đồng biến nghịch biến hay không, ta có thể dùng cách này để "thử trước", nếu không phải hàm đồng biến hay nghịch biến thì kiếm cách khác đỡ mất thời gianVí dụ 1: Ta sử dụng tính năng TABLE tương tự như phần trình bày ở trênMODE 7 nhập bấm = -14=15=1= Máy hiện ta kéo xuống thì thấy với X chạy từ -14 đến 15 thì F(x) có giá trị tăng dần và X=0 là nghiệm. Ta đoán hàm trên là 1 hàm đồng biến, từ đó ta có thể nghĩ tới cách đạo hàm. Đây chỉ là 1 ví dụ đơn giản nên có thể không cần bấm máy nhưng trong nhiều bài toán phức tạp, nhiều lúc ta cố gắng chứng minh hàm đồng biến nghịch biến để giải mà trong khi hàm đó hoàn toàn không đồng nghịch biến gì hết thì quả thật mất công. Có nhiều trường hợp cũng nên cẩn thận, có thể hàm là đồng/nghịch biến nhưng bạn không thể làm chứng minh hàm đồng biến nghịch biến được, lúc đó, bạn nên nghĩ cách khácNếu bạn nào muốn tham khảo bài viết này của mình để chia sẻ hoặc sáng tạo thêm để đăng trên các website diễn đàn khác nên liên hệ trước qua facebook của mình hoặc ghi thêm "tham khảo Trần Ngọc Ánh Phương - kinhnghiemhoctap.blogspot.com"

CÁCH TÍNH PHƯƠNG TRÌNH BẬC HAI CHỨA CĂN TRÊN CASIO FX570ES

Cái này chắc nhiều bạn biếtVÍ DỤ: giải phương trình x²+5x+3 =01,Các bạn nhập biểu thức này: (đảm bảo chưa đầy 4 giây nếu quen)

2,Bấm [CALC]3,Lần lượt nhập các hệ số b,c,a (bấm [5][=][1][=][3][=]), màn hình xuất hiện nghiệm thứ nhất

4,các bạn bấm [>][>][-][=] các bạn có nghiệm thứ hai!

TÍNH UCLN BCNN hai số A,B

cách 1 (số đơn giản) (trích từ sách hướng dẫn sử dụng fx 500ms) ví dụ ta tìm UCLN và BCNN của 20 và 25, lấy , kết quả tính BCNN: lấy 25*4 hoặc 20*5 (nhân chéo) => BCNN=100tính UCLN: lấy 25/5 hoặc 20/4 (chia thẳng hàng) => UCLN=5cách 2 ( số quá lớn)http://www.bitex.com.vn/kho-ung-dung/1237/tim-uoc-chung-lon-nhat-giai-tren-mt-casio-fx-570ms.html

KIỂM TRA XEM MỘT SỐ CÓ PHẢI LÀ SỐ NGUYÊN TỐ HAY KHÔNG?

Cái này biết cho vui vậy thôi chứ cũng không cần thiết lắm, chương trình ít đụng tới cái này. Tuy nhiên mình thấy cách người ta đưa ra phải bấm phím "bằng" liên tục cho tới khi ra kết quả thì thôi. Như vậy theo mình rất mất thời gian (rất là với các số lớn). Vì vậy mình xin đưa ra cách riêng của mình để giải bài toán này, cách của mình thì chỉ cần bấm bằng một lần để ra đáp án thôi. Các bạn làm theo như sau nhé!

  • bấm shift mode 6 0
  • nhập biểu thức

Cách bấm như sau: shift , nhập,(lưu ý nhập Rnd() bằng cách bấm shift 0). Bấm phím sang phải, nhập 2, sang phải, nhập Rnd(√A)

  • bấm CALC, nhập số cần kiểm tra, [=] [=]
  • nếu máy hiện math error nghĩa là số này không phải là số nguyên tố
  • nếu máy hiện một kết quả bất kỳ có nghĩa là số trên là một số nguyên tố
  • sau khi hoàn thành xong, bạn bấm shift 9 3 = để máy về lại chế độ ban đầu

Tìm căn bậc hai số phức trên fx570esCái này tớ xem trên Kênh Thiên Tứ Youtube http://www.youtube.com/watch?v=QfBDr-UCQKoTớ xin trình bày lại như sauVí dụ tìm căn bậc hai của -3-4ibấm mode 2 (cmplx)bấm -3-4i =bấm căn shift hyp ans > > shift âm phân số shift 21 ans ) > 2 =cụ thể như hình saumáy hiện 1-2i, vậy kết quả là 1-2i và -1+2i

CÁCH GIẢI SƠ ĐỒ CHÉO HOÁ HỌC

Ta xét ví dụ sau: một dung dịch HCl nồng độ 35% và một dung dịch HCl khác có nồng độ 15%. Để có dung dịch có nồng độ là 20% thì cần phải pha chế hai dung dịch trên với tỉ lệ bao nhiêu?A.1/3 B.3/1 C.1/5 D.5/1GiảiThông thường ta sẽ vẽ sơ đồ đường chéo ra với dạng như sau35 20-15=5 2015 35-20=15=> tỉ lệ là 5/15=1/3 => A đúngBây giờ ta sẽ thử áp dụng cách bấm máy nhanh thay cho cách thông thường như trênB1: chuyển máy sang chế độ giải hệ phương trình 2 ẩn. MODE 5 1B2: Nhập số liệu bài toán 35= 15= 20=B3: Nhập 1= 1= 1= =, ra kết quả x=1/4 và y=3/4B4: Lấy x/y = 1/3 => A đúng (chú ý do x và y đều có mẫu chung nên chỉ cần lấy tử chia cho nhau là được, hầu hết các bài toán thực tế đều ra kết quả chung mẫu)Có thể bạn nghĩ rằng cách bấm máy này hơi phức tạp nhưng thực sự là do mình phải giải thích cho các bạn nên có thể hơi dài dòng. Với cách giải thông thường bạn phải bấm máy 3 lần. Lần đầu 35-20, lần hai 20-15, lần ba 5/15. Trong khi cách giải này chỉ bấm máy một lần là nhìn ra kết quả 1/3 VD2:2 4 2428 22=> 4/22 = 2/11* bấm máy MODE 51 2=28=24= 1=1=1=ra 2/13 và 11/13 => đáp án 2/11

Nếu các bạn có ý kiến gì về bài viết của mình thì hãy comment bên dưới, không cần đăng kí gì đâu ^.^

TIN KHÁC

  • » Gia sư môn toán
  • » Đề, đáp án môn Toán thi thử lần 2 liên trường THPT Nghệ An 2019
  • » Gia sư môn toán lớp 1-12 tại thành phố Vinh và phụ cận
  • » Phương pháp dạy học toán cho học sinh trung bình - Gia sư Toán giỏi tại Vinh
  • » Phương pháp học toán hiệu quả - Gia sư toán lớp 1 2 3 5 5 6 7 8 910 11 12 tại Vinh
  • » Gia sư Toán Lý, Hoá cho học sinh lớp 12, LTĐH tại thành phố VInh
  • » Tớ đã học Toán để thi Đại học như thế nào? Gia sư toán tại thành phố Vinh
  • » Gia sư toán lớp 10 tại Vinh - phần mệnh đề
  • » Gia sư lớp toán tại tp vinh - Toán 10 HÀM SỐ. TẬP XÁC ĐỊNH – ĐỒ THỊ
  • » Gia sư toán lớp 10 tại Vinh - KHÁI NIỆM VỀ PHƯƠNG TRÌNH
  • » Gia sư toán 10 tại thành phố Vinh - Phương trình
  • » Gia sư toán lớp 10 ở thành phố Vinh - Bất đẳng thức
  • » Gia sư toán 10 tại Vinh - Thống kê
  • » Dạy kèm toán lớp 10 tại Vinh - Lượng giác
  • » Gia sư toán lớp 11 tại thành phố Vinh - Phương trình lượng giác
  • » Gia sư toán 11 tại Vinh - Tổ hợp và xác suất
  • » Gia su taon 11 tai Vinh - Dãy số, cấp số
  • » Gia sư toán lớp 11 - Giới hạn dãy số
  • » Gia sư toán lớp 11 tại TP Vinh - Giới hạn của hàm số
  • » Gia sư toan 11 tai tp Vinh - Tính liên tục của hàm số
  • » Gia sư toán 10 tại thành phố Vinh - Đạo hàm
  • » Gia sư toán 11 tại Vinh - Phép biến hình phần 1
  • » Gia su toan 11 tai Vinh - Phép biến hình phần 2
  • » Gia sư toán 11 tại Vinh - Phép biến hình phần 3
  • » Gia sư Toán 11 tại Vinh - Đường thẳng và mặt phẳng
  • » Gia sư toán lớp 11 tại thành phố Vinh -Hai đường thẳng song song
  • » Gia su toan 11 tai Vinh - Đường thẳng song song mặt phẳng
  • » Tìm gia sư toán 11 tại Vinh - Hai mặt phẳng song song
  • » Những công thức toán học cần nhớ - Gia sư môn Toán lớp 1 2 3 4 5 6 7 8 9 10 11 12 tại Vinh
  • » Gia sư toán 10 tại Vinh - Tập hợp
  • » Gia sư lớp 10 ở tp Vinh - Hàm số thực
  • » Toán 10 thành phố Vinh - Hàm lượng giác cơ bản
  • » Gia sư toán lớp 10 ở tp Vinh - Hàm lượng giác ngược
  • » Gia sư toán 10 tại Vinh - Hàm số mũ và logarit
  • » Gia sư toán lớp 10 tại Vinh - Mệnh đề
  • » Gia sư lớp 10 ở tp Vinh - Tập hợp
  • » Gia sư toán 10 tại tp Vinh - Hàm số
  • » Gia sư toán lớp 10 tại thành phố Vinh - Phương trình
  • » Dạy kèm toán 10 tại thành phố Vinh - Hệ phương trình
  • » Gia sư toán lớp 10 thành phố Vinh - Bất đẳng thức
  • » Gia sư toán 10 tại tp Vinh - Bất đẳng thức Cô si
  • » Gia sư toán lớp 10 tại Vinh - BĐT chứa dấu GTTĐ
  • » Gia sư lớp 10 ở tp Vinh - Bất đẳng thức Bu–nhia–cốp–xki
  • » Gia sư lớp 10 ở tp Vinh - ỨNG DỤNG BẤT ĐẲNG THỨC TÌM GTLN VÀ GTNN
  • » Gia sư toán tại Vinh - Bài tập nâng cao BĐT
  • » Gia sư toán 10 tại Vinh - PT, BPT
  • » Gia sư toán 10 tại thành phố Vinh - Phương trình - Bất phương trình
  • » Gia sư toán lớp 10 tại thành phố Vinh - Thống kê
  • » Gia sư toán lớp 10 tại Vinh - Vec tơ phần 1
  • » Gia sư toán lớp 10 tại Vinh - Vec tơ phần2
  • » Gia sư toán lớp 10 - Vec tơ phần 3
  • » Gia su toan 10 tai Vinh - Tích vô hướng của 2 véc tơ P1
  • » Gia su toan 10 tai Vinh - Tích vô hướng của 2 véc tơ P2
  • » Gia su toan 10 tai Vinh - Phương trinh dương thang
  • » Gia su toan 10 tai Vinh - Phương trinh dương tron
  • » Gia su toan 10 tai Vinh - Elip
  • » Gia sư toán lớp 11 tại thành phố Vinh - Hàm số ượng giác
  • » Tìm gia sư toán 11 tại Vinh - Vec tơ trong không gian
  • » Gia sư toán 11 tại Vinh - Hai đường thảng vuông góc
  • » Gia sư toán 12 tại Vinh - Khảo sát hàm số và ứng dụng đồ thị hàm số
  • » Gia sư toán lớp 12 tại TP Vinh - Đạo hàm và ứng dụng
  • » Gia sư Toán tại Vinh -Đạo hàm và ứng dụng P3
  • » Gia sư toán 12 tại tp Vinh - PT mũ - logarit
  • » Mẹo làm bài thi tốt nghiệp môn Toán đạt điểm cao
  • » Dạng bài tập dễ xuất hiện trong đề thi ĐH môn Toán
  • » Môn Toán: Học sinh chỉ nháp ra giấy nội dung khó
  • » Yếu tố nào quyết định BẠN đạt điểm cao môn toán
  • » Mẹo làm bài thi tốt nghiệp môn Toán đạt điểm cao
  • » Phân tích, dự đoán cấu trúc đề thi tốt nghiệp THPT mônToán
  • » Phân tích đề Toán trước khi vào phòng thi
  • » Cách giải khác của câu hỏi hóc búa nhất trong đề Toán
  • » Phổ điểm Toán đề thi đại học khối A, A1 2014 ở khoảng 5-6
  • » Giải câu hệ phương trình khối A năm 2014 bằng nhiều cách
  • » Giải đề Toán khối A 2014 bằng nhiều cách
  • » Mời bạn đọc xem gợi ý bài giải môn Toán khối B, khối D kỳ thi ĐH đợt 2.
  • » 11 cách giải cho câu hình học phẳng (câu 7) khối A 2014
  • » Làm đúng nhưng khác đáp án, có được điểm ?
  • » Bài giải môn toán, kỳ thi cao đẳng 2014
  • » Ôn thi đại học môn Toán: Tổ hợp và xác suất
  • » Đề thi kiểm tra năng lực
  • » Ôn thi đại học môn Toán: Cực trị của hàm số
  • » Tính nhân bằng giao điểm
  • » 7 mẹo tính toán mà chúng ta không được học ở trường
  • » Các dạng toán về xác suất
  • » Đề, đáp thi thử Đại học môn Toán
  • » Phương pháp viết phương trình tiếp tuyến
  • » Phương pháp đồng bậc để giải hệ phương trình
  • » 3 lỗi trình bày mất điểm như chơi khi làm bài thi môn Toán
  • » 9 bài học giúp học sinh vượt qua các bài toán chứng minh hình học
  • » 12 phương pháp chứng minh bất đẳng thức
  • » Bí kíp sử dụng máy tính casio "triệt hạ" câu Hệ phương trình
  • » Đáp án đề thi THPT quốc gia môn Toán năm 2015 mới nhất (cập nhật)
  • » 199 bài tập hệ phương trình có đáp án- luyện thi THPT Quốc Gia
  • » Tuyển chọn 20 đề thi thử các trường chuyên có đáp án thang điểm chi tiết
  • » Tuyển tập đề thi vào 10 các tỉnh năm học 2013 - 2014
  • » Bài toán "Kim đồng hồ"
  • » Nội dung ôn tập thi THPT 2018
  • » Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
  • » 14 tính chất hình học mặt phẳng giúp bạn lấy điểm tối đa
  • » Công thức tính diện tích và thể tích các hình khối cơ bản
  • » Đề cương ôn tập học kỳ 1 lớp 12 - THPT Huỳnh Thúc Kháng Vinh
  • » Đề cương ôn tập học kỳ 1 lớp 11 - THPT Chuyên Vinh
  • » Đề ôn tập học kỳ 1 lớp 12 - Vinh 1
  • » Đề cương ôn tập học kỳ 1 lớp 12 - THPT Lê Viết Thuật
  • » Đề cương ôn tập học kỳ 1 lớp 12
  • » Khoảng cách giữa hai đường chéo nhau
  • » Tại sao cơ số của lũy thừa với số mũ hữu tỉ phải dương?
  • » Bài 2. Phép đối xứng qua mặt phẳng – HH12 NC
  • » Đề thi thử Toán THPT Quốc gia 2019 lần 3 trường THPT chuyên ĐHSP Hà Nội
  • » Bộ đề thi thử THPT 2019 - Môn Toán (Đáp án chi tiết)
  • » Bộ đề chống liệt môn Toán thi THPT 2019
  • » Giải chi tiết đề Toán thi thử lần 3 Chuyên ĐH Vinh
  • » Đáp án, đề thi thử THPT quốc gia lần 1 năm 2020 của liên trường THPT tỉnh Nghệ An

Từ khóa » Cách Bấm Casio Tính Lim