Cách Viết Phương Trình Tiếp Tuyến Khi Biết Hệ Số Góc K - Toán Lớp 11
Có thể bạn quan tâm
Vậy cách viết phương trình tiếp tuyến khi có hệ số góc k như thế nào? nội dung toán 11 phần đạo hàm sẽ hướng dẫn chúng ta cách làm bài toán này, chúng ta hãy cùng tìm hiểu ở bài viết này.
• Cách viết phương trình tiếp tuyến khi biết hệ số góc k
- Gọi (Δ) là tiếp tuyến cần tìm có hệ số góc k.
- Giả sử M(xo ; yo) là tiếp điểm. Khi đó xo thỏa mãn: f'(xo) = k; (*)
- Giải phương trình (*) tìm tìm được xo. khi đó tính: yo = f(xo)
- Phương trình tiếp tuyến cần tìm là: y = k( x - xo) + yo
> Chú ý:
- Số tiếp tuyến của đồ thị chính là số nghiệm của phương trình : f’(x) = k
- Cho hai đường thẳng d1 : y = k1x + b1 và d2 : y = k2x + b2. (k1; k2 là hệ số góc của các đường thẳng d1 và d2), khi đó:
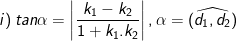
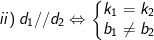
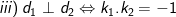
- Đường thẳng d: y = kx + b tạo với trục hoành một góc α thì: k = ±tanα.
• Bài tập viết phương trình tiếp tuyến khi biết hệ số góc k
* Ví dụ 1 (Bài 5 trang 156 SGK Đại số 11): Viết phương trình tiếp tuyến đường cong y=x3.
a) Tại điểm (-1; -1);
b) Tại điểm có hoành độ bằng 2;
c) Biết hệ số góc của tiếp tuyến bằng 3.
* Lời giải:
* Với mọi x0 ∈ R thì:
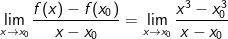
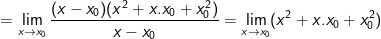
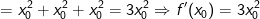
a) Tiếp tuyến của y = x3 tại điểm (-1; -1) là:
y = f’(-1)(x + 1) + y(1)
= 3.(-1)2(x + 1) – 1
= 3.(x + 1) – 1
= 3x + 2.
b) Tại điểm có hoành độ: x0 = 2
⇒ y0 = f(2) = 23 = 8;
⇒ f’(x0) = f’(2) = 3.22 = 12.
⇒ Vậy phương trình tiếp tuyến của y = x3 tại điểm có hoành độ bằng 2 là :
y = 12(x – 2) + 8 = 12x – 16.
c) Biết hệ số góc của tiếp tuyến k = 3
⇔ f’(x0) = 3 ⇔ 3x02 = 3
⇔ x02 = 1 ⇔ x0 = ±1.
+ Với x0 = 1 ⇒ y0 = 13 = 1
⇒ Phương trình tiếp tuyến: y = 3.(x – 1) + 1 = 3x – 2.
+ Với x0 = -1 ⇒ y0 = (-1)3 = -1
⇒ Phương trình tiếp tuyến : y = 3.(x + 1) – 1 = 3x + 2.
→ Vậy có hai phương trình tiếp tuyến của đường cong y = x3 có hệ số góc bằng 3 là y = 3x – 2 và y = 3x + 2.
* Ví dụ 2 (Bài 6 trang 156 SGK Đại số 11): Viết phương trình tiếp tuyến của hypebol y = 1/x.
a) Tại điểm (1/2; 2)
b) Tại điểm có hoành độ bằng -1;
c) Biết hệ số góc của tiếp tuyến bằng -1/4
* Lời giải:
* Với mọi x0 ∈ R\{0} thì:
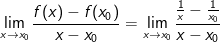
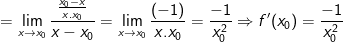
a) Tại điểm (1/2; 2)
- Ta có: 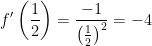
- Do đó phương trình tiếp tuyến của hypebol tại điểm (1/2;2) là:
y = f'(x0)(x - x0) + y0 = -4(x - 1/2) + 2 = -4x + 4
b) Tại điểm có hoành độ bằng -1;
- Tại x0 = -1 ⇒ y0 = -1 ⇒ f’(x0) = -1.
⇒ Vậy phương trình tiếp tuyến của đường cong y = 1/x tại điểm có hoành độ -1 là: y = -1(x + 1) – 1 = -x – 2.
c) Biết hệ số góc của tiếp tuyến bằng -1/4.
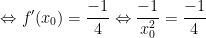
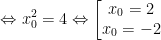
+ Với x0 = 2 ⇒ y0 = 1/x0 = 1/2;
⇒ Phương trình tiếp tuyến là: 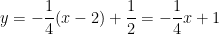
+ Với x0 = -2 ⇒ y0 = 1/x0 = -1/2;
⇒ Phương trình tiếp tuyến là: 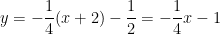
⇒ Vậy có hai phương trình tiếp tuyến của hypebol y = 1/x có hệ số góc -1/4 là: 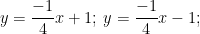
Từ khóa » Ct Hệ Số Góc K
-
Cách Tính Hệ Số Góc Của đường Thẳng, Bài Tập áp Dụng - Thủ Thuật
-
Cách Tính Hệ Số Góc K Của Tiếp Tuyến Với Đồ ... - Thánh Chiến 3D
-
Hệ Số Góc Của đường Thẳng - Thầy Phú
-
Cách Tính Hệ Số Góc Của đường Thẳng - Thủ Thuật Phần Mềm
-
Hệ Số Góc Của đường Thẳng: Cách Tính Và Bài Tập - Mobitool
-
Hệ Số Góc Là Gì? - O₂ Education
-
Công Thức Tính Hệ Số Góc - Phê Bình Văn Học
-
Hệ Số Góc K Của Phương Trình Tiếp Tuyến
-
Hệ Số Góc Của đường Thẳng: Cách Tính Và Bài Tập ...
-
Viết Phương Trình Tiếp Tuyến Của đồ Thị Hàm Số (C): Y = F(x) Có Hệ Số ...
-
Hệ Số Góc Của đường Thẳng Trong Mặt Phẳng - Toán Thầy Định
-
Cách Tính Hệ Số Góc Của đường Thẳng - GG - Information
-
Cách Viết Phương Trình đường Thẳng Khi Biết Hệ Số Góc Hay, Chi Tiết
-
Cách để Tính Hệ Số Góc, Tung Và Hoành độ Gốc Của đường Thẳng