[Chia Sẻ] Đề Thi HSG Toán Thường 12 TPHCM 2019-2020

• Diễn đàn Bài viết mới Tìm kiếm trên diễn đàn
• Đăng bài nhanh
• Có gì mới? Bài viết mới New media New media comments Status mới Hoạt động mới
• Thư viện ảnh New media New comments Search media
• Story
• Thành viên Đang truy cập Đăng trạng thái mới Tìm kiếm status cá nhân

Đăng nhập Đăng ký

Tìm kiếm

Everywhere Đề tài thảo luận This forum This thread Chỉ tìm trong tiêu đề By: Search Tìm nâng cao… Everywhere Đề tài thảo luận This forum This thread Chỉ tìm trong tiêu đề By: Search Advanced…

• Bài viết mới
• Tìm kiếm trên diễn đàn

Menu Install the app Install Toán 12[Chia sẻ] Đề thi HSG Toán thường 12 TPHCM 2019-2020

• Thread starter iceghost
• Ngày gửi 10 Tháng sáu 2020
• Replies 3
• Views 9,444

• Bạn có 1 Tin nhắn và 1 Thông báo mới. [Xem hướng dẫn] để sử dụng diễn đàn tốt hơn trên điện thoại

• Diễn đàn
• TOÁN
• TRUNG HỌC PHỔ THÔNG
• Toán lớp 12
• Thảo luận chung

You are using an out of date browser. It may not display this or other websites correctly.You should upgrade or use an alternative browser.

iceghost

Cựu Mod Toán

Thành viên TV BQT xuất sắc nhất 2016 20 Tháng chín 2013 5,018 7,484 941 TP Hồ Chí Minh Đại học Bách Khoa TPHCM [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Môn thi: Toán Thời gian làm bài: 120 phút Bài 1. (4 điểm) Giải phương trình: $4^{\log_{2020} x} + \log_2 (-2 + x^{\log_{2020} 4}) = 2^{\log_{2020} x} + \log_{2020} x + 2$. Bài 2. (4 điểm) Cho hàm số $y = \dfrac{x + 2}{x - 1}$ có đồ thị $(C)$. Gọi $d$ là đường thẳng di động đi qua điểm $I(1; 1)$ và cắt $(C)$ tại hai điểm $M$, $N$. Tính khoảng cách từ điểm $A(2; -3)$ đến $d$ khi tam giác $AMN$ có diện tích nhỏ nhất. Bài 3. (4 điểm) Cho hình lăng trụ $ABC.A'B'C'$, khoảng cách từ $A'$ đến $BB'$ và $CC'$ lần lượt bằng $\sqrt{3}$ và $2$, góc giữa hai mặt phẳng $(BCC'B')$ và $(ACC'A')$ bằng $60^\circ$. Hình chiếu vuông góc của $A$ lên mặt phẳng $(A'B'C')$ là trung điểm $M$ của $B'C'$ và $A'M = \sqrt{13}$. a) Tính khoảng cách từ $M$ đến $AA'$. b) Tính thể tích của khối lăng trụ $ABC.A'B'C'$​ Bài 4. (4 điểm) Cho hàm số $f(x) = \dfrac12 x^2 - mx$ và $g(x) = \dfrac{x - m}{x - 1}$, tham số $m \ne 1$, có đồ thị $(C_1)$, $(C_2)$. Biết rằng tồn tại đúng $2$ số $x_0 \in (2; 3)$ sao cho nếu gọi $d_1$, $d_2$ là tiếp tuyến tại các điểm có hoành độ $x_0$ thuộc $(C_1)$, $(C_2)$ và $d_1$, $d_2$ cắt nhau tại $A$, còn $d_1$, $d_2$ cắt trục $Ox$ ở $B$, $C$ thì $AB = AC$. Tìm tất cả các giá trị $m$. Bài 5. (4 điểm) Cho tập hợp $X = \left\{ x | x \in \mathbb{Z}, -5 \leq x \leq 5, x \ne 0 \right\}$. Chọn ngẫu nhiên $4$ số đôi một phân biệt $a$, $b$, $c$, $d \in X$. Tính xác suất để hàm số $y = \dfrac{ax + b}{cx + d}$ với $ad \ne bc$, có đồ thị $(C)$ mà cả $(C)$ lẫn tiệm cận đứng của $(C)$ đều cắt trục $Ox$ theo chiều dương. -- Hết --​

• 

Reactions: Dat_06, Kkkkkkkkk 46789, Bella Dodo and 4 others

iceghost

Cựu Mod Toán

Thành viên TV BQT xuất sắc nhất 2016 20 Tháng chín 2013 5,018 7,484 941 TP Hồ Chí Minh Đại học Bách Khoa TPHCM Lời giải: thực hiện bởi iceghost 1/ ĐK: $x > 0$ và $x^{\log_{2020} 4} > 2$ Đặt $t = \log_{2020} x$ pt $\iff 4^t + \log_2 (-2 + 4^t) = 2^t + t + 2$ $\iff 4^t - 2 + \log_2 (4^t - 2) = 2^t + t$ Xét hàm $f(a) = 2^a + a$ trên $\mathbb{R}$ $f'(a) = 2^a \ln 2 + 1 > 0 \, \forall a \in \mathbb{R}$ Suy ra $f(a)$ đồng biến trên $\mathbb{R}$ pt $\iff f(\log_2 (4^t - 2)) = f(t)$ $\iff \log_2 (4^t - 2) = t$ $\iff 4^t - 2 = 2^t$ $\iff (2^t - 2)(2^t + 1) = 0$ $\iff t = 1$ $\iff x = 2020$ (N) Vậy $x = 2020$ là nghiệm pt 2/ $(C) : y = \dfrac{x + 2}{x - 1}$ ($x \ne 1$) Đường thẳng qua $I(1, 1)$ có dạng $d: y = m(x - 1) + 1 = mx - m + 1$ PT hoành độ giao điểm: $\dfrac{x + 2}{x - 1} = mx - m + 1$ $\iff mx^2 - 2mx + m - 3 = 0$ $x = 1$ không là nghiệm pt. Để pt có 2 nghiệm phân biệt thì $\begin{cases} m \ne 0 \\ \Delta' = m^2 - m(m - 3) = 3m > 0 \end{cases} \iff m > 0$ Giả sử pt có 2 nghiệm $x_1$, $x_2$ thì $M(x_1, mx_1 - m + 1)$, $N(x_2, mx_2 - m + 1)$ $\vec{AM} (x_1 - 2, mx_1 - m + 4)$ $\vec{AN} (x_2 - 2, mx_2 - m + 4)$ $S_{AMN} = \dfrac12 \left| (x_1 - 2)(mx_2 - m + 4) - (x_2 - 2)(mx_1 - m + 4) \right|$ $= \dfrac12 \left| (m + 4)(x_1 - x_2) \right|$ $= \dfrac12 \sqrt{(m + 4)^2 [(x_1 + x_2)^2 - 4x_1 x_2] }$ $= \dfrac12 \sqrt{(m + 4)^2 ( 4 - 4 \cdot \dfrac{m - 3}m )}$ $= \sqrt{\dfrac{3(m + 4)^2}{m}}$ $= \sqrt{3m + 24 + \dfrac{48}m}$ $\geqslant \sqrt{2 \sqrt{3m \cdot \dfrac{48}m} + 24} = 4 \sqrt{3}$ Dấu '=' xảy ra khi $3m = \dfrac{48}m$ hay $m = 4$ (do $m > 0$) Khi đó $d : y = 4x - 3$ $d(I, d) = \dfrac{|4 \cdot 2 + 3 - 3|}{\sqrt{4^2 + 1^2}} = \dfrac{8}{\sqrt{17}}$ 4/ $(C_1) : y = f(x) = \dfrac12 x^2 - mx$ $(C_2) : y = g(x) = \dfrac{x - m}{x - 1}$ Để ba điểm $A$, $B$, $C$ thỏa mãn $AB = AC$ thì hệ số góc của $d_1$ và $d_2$ phải là hai số đối nhau $\iff f'(x_0) = -g'(x_0)$ $\iff x_0 - m = \dfrac{1 - m}{(x_0 - 1)^2}$ $\iff x_0(x_0 - 1)^2 - 1 = m[(x_0 - 1)^2 - 1]$ $\iff m = \dfrac{x_0 (x_0 - 1)^2 - 1}{(x_0 - 1)^2 - 1} = x_0 + \dfrac{x_0 - 1}{(x_0 - 1)^2 - 1}$ Xét $h(x_0) = x_0 + \dfrac{x_0 - 1}{(x_0 - 1)^2 - 1}$ $h'(x_0) = 1 + \dfrac{(x_0 - 1)^2 - 1 - 2(x_0 - 1)^2}{[(x_0 - 1)^2 - 1]^2} = 0$ $\iff (x_0 - 1)^2 + 1 = [(x_0 - 1)^2 - 1]^2$ $\iff (x_0 - 1)^4 - 3(x_0 - 1)^2 = 0$ $\iff x_0 = 1 \vee x_0 = 1 + \sqrt{3} \vee x_0 = 1 - \sqrt{3}$ $ \begin{array}{c|ccccc} x_0 & 2 & & 1+\sqrt{3} & & 3 \\ \hline h'(x_0) & & - & 0 & + \\ \hline h(x_0) & +\infty & & & & \dfrac{11}3 \\ & & \searrow & & \nearrow & \\ & & & \dfrac{2 + 3\sqrt{3}}2 & & \end{array} $ Để có đúng 2 số $x_0 \in (2, 3)$ thỏa đề thì $\dfrac{2 + 3\sqrt{3}}2 < m < \dfrac{11}3$

• 

Reactions: Bella Dodo, TranPhuong27, dangtiendung1201 and 1 other person

iceghost

Cựu Mod Toán

Thành viên TV BQT xuất sắc nhất 2016 20 Tháng chín 2013 5,018 7,484 941 TP Hồ Chí Minh Đại học Bách Khoa TPHCM 3/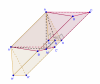 (Nếu bạn muốn vọc vạch trên ggb thì file ở đây: https://www.geogebra.org/m/hedrqq77) a) Hạ $AH \perp BB'$ và $AK \perp CC'$ thì $AH = \sqrt{3}$ và $AK = 2$. Do $BB' \parallel CC'$ nên $(AHK) \perp CC'$, suy ra $HK \perp CC'$ Khi đó $((BCC'B'), (ACC'A')) = \widehat{AKH} = 60^\circ$ Xét $\triangle{AHK}$: $AH^2 = KA^2 + KH^2 - 2 KA \cdot KH \cdot \cos 60^\circ$ $\iff 3 = 4 + KH^2 - 2KH$ $\iff KH = 1$ Gọi $N$ là trung điểm $HK$ thì theo tính chất đường trung bình: $MN \parallel BH \parallel AA'$ Suy ra $d(M, AA') = d(N, AA') = NA$ (do $(AHK) \perp AA'$ nên $AN \perp AA'$) $= \sqrt{AH^2 + HN^2} = \dfrac{\sqrt{13}}2$ b) Hạ $A'H' \perp BB'$ và $A'K' \perp CC'$. Khi đó dễ thấy khối chóp $A.BCKH$ bằng khối chóp $A'.B'C'K'H'$ Suy ra $V_{ABC.A'B'C'} = V_{AHK.A'H'K'} = AA' \cdot S_{AHK}$ Xét $\triangle{AMA'}$ vuông tại $M$: $\dfrac1{d^2(M, AA')} = \dfrac1{MA^2} + \dfrac1{MA'^2} \implies MA = \dfrac{\sqrt{13}}{\sqrt{3}}$ $AA' = \sqrt{MA'^2 + MA^2} = \dfrac{2\sqrt{39}}3$ Có $S_{AHK} = \dfrac12 KA \cdot KH \cdot \sin 60^\circ = \dfrac{\sqrt{3}}2$ Từ đó $V_{ABC.A'B'C'} = \sqrt{13}$ 5/ Tác giả vẫn chưa nghĩ ra lời giải nào đẹp. Tạm thời dùng cách liệt kê: Mã: // JavaScript const X = [-5, -4, -3, -2, -1, 1, 2, 3, 4, 5]; const kgm = []; const bienco = []; for (let a of X) { for (let b of X) { for (let c of X) { for (let d of X) { if (a === b || a === c || a === d || b === c || b === d || c === d) continue; kgm.push([a, b, c, d]); if (a * d === b * c) continue; if (a * b < 0 && c * d < 0) bienco.push([a, b, c, d]); } } } } console.log(bienco.length, kgm.length); (Nếu thích bạn có thể F12 trình duyệt rồi paste vào console để chạy thử) Nếu như mình lập trình đúng thì biến cố là $1472$ và không gian mẫu là $5040$. Xác suất là $\dfrac{92}{315}$ Còn đây là lời giải của thầy có facebook là Phong Lâm Hứa, đăng tải trên Facebook... Last edited: 3 Tháng chín 2020

• 

Reactions: Haru Bảo Trâm, Bella Dodo and dangtiendung1201

System32

Học sinh chăm học

Thành viên 25 Tháng chín 2018 343 348 101 Hà Nội THPT Marie Curie

iceghost said: 5/ Tác giả vẫn chưa nghĩ ra lời giải nào đẹp. Tạm thời dùng cách liệt kê: Mã: // JavaScript const X = [-5, -4, -3, -2, -1, 1, 2, 3, 4, 5]; const kgm = []; const bienco = []; for (let a of X) { for (let b of X) { for (let c of X) { for (let d of X) { if (a === b || a === c || a === d || b === c || b === d || c === d) continue; kgm.push([a, b, c, d]); if (a * d === b * c) continue; if (a * b < 0 && c * d < 0) bienco.push([a, b, c, d]); } } } } console.log(bienco.length, kgm.length); Bấm để xem đầy đủ nội dung ...

Tiện thể em cũng làm một code tương tự với Python:> Mã: from math import * all_event = 0 specific = 0 for a in range(-5, 6): for b in range(-5, 6): for c in range(-5, 6): for d in range(-5, 6): if a == 0 or b == 0 or c == 0 or d == 0: pass else: X = [a, b, c, d] if len(set(X)) == 4: all_event += 1 if a * d != b * c and a * b < 0 and c * d < 0: specific += 1 else: continue print('Probability: {} % ({}/{})'.format(100*specific/all_event, specific, all_event)) And it works perfectly fine...

• 

Reactions: Bella Dodo, Quân (Chắc Chắn Thế) and giangha13062013 You must log in or register to reply here. Chia sẻ: Facebook Reddit Pinterest Tumblr WhatsApp Email Chia sẻ Link

• Diễn đàn
• TOÁN
• TRUNG HỌC PHỔ THÔNG
• Toán lớp 12
• Thảo luận chung

Top Bottom

• Vui lòng cài đặt tỷ lệ % hiển thị từ 85-90% ở trình duyệt trên máy tính để sử dụng diễn đàn được tốt hơn.