Cho A,b,c > 0 CMR A3/b B3/c C3/a >= Ab Bc Ca - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
- Hattori Heiji
Cho a,b,c >0 CMR a3/b+b3/c+c3/a>=ab+bc+ca
Mong mọi người giải chi tiết
Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 2 2
Gửi Hủy 
Pham Quoc Cuong 10 tháng 4 2018 lúc 21:05 Cách khác dễ hiểu hơn
Áp dụng BĐT Cô si 2 số ko âm
Ta có: \(\frac{a^3}{b}+ab\ge2\sqrt{a^4}=2a^2\)
Tương tự rồi sau đó lại có:
\(\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}+ab+bc+ca\ge2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ca\right)\)
\(\Rightarrow\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge ab+bc+ca\)
Đúng 2 Bình luận (0) Gửi Hủy Pham Quoc Cuong 10 tháng 4 2018 lúc 20:07 Áp dụng BĐT Cô si với 3 số k âm
\(\frac{a^3}{b}+\frac{a^3}{b}+b^2\ge\frac{3\sqrt[3]{a^3.a^3.b^2}}{b^2}=3a^2\)
\(\frac{b^3}{c}+\frac{b^3}{c}+b^2\ge3b^2\)
\(\frac{c^3}{a}+\frac{c^3}{a}+c^2\ge3c^2\)
\(\Rightarrow2\left(\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\right)+a^2+b^2+c^2\ge3\left(a^2+b^2+c^2\right)\)
\(\Rightarrow\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge a^2+b^2+c^2\)
Mà \(a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge ab+bc+ca\)
Đúng 3 Bình luận (0) Gửi Hủy 
- Jess Nguyen
CMR: 2(a3 + b3 + c3) + 3abc ≥ ab + bc + ca biết a + b + c = 1 và a, b, c dương
Xem chi tiết Lớp 8 Toán 1 0
Gửi Hủy 
Nguyễn Việt Lâm CTV 
3 tháng 3 2022 lúc 0:01 Do \(a+b+c=1\) nên BĐT cần chứng minh tương đương:
\(2\left(a^3+b^3+c^3\right)+3abc\ge\left(ab+bc+ca\right)\left(a+b+c\right)\)
\(\Leftrightarrow2\left(a^3+b^3+c^3\right)\ge ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\)
Thật vậy, ta có:
\(2\left(a^3+b^3+c^3\right)=\left(a^3+b^3\right)+\left(b^3+c^3\right)+\left(c^3+a^3\right)\)
\(=\left(a+b\right)\left(a^2+b^2-ab\right)+\left(b+c\right)\left(b^2+c^2-bc\right)+\left(c+a\right)\left(c^2+a^2-ca\right)\)
\(\ge\left(a+b\right)\left(2ab-ab\right)+\left(b+c\right)\left(2bc-bc\right)+\left(c+a\right)\left(2ca-ca\right)\)
\(=ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Đúng 0 Bình luận (0) Gửi Hủy 
- Lelemalin
Bài 1:
a) Cho a + b + c = 0. CMR: a3 + b3+ c3 = 3abc
b) Cho a3 + b3 + c3 = 3abc và a. b, c đôi một khác nhau. CMR: a + b + c = 0
Xem chi tiết Lớp 8 Toán 3 0 Gửi Hủy 
Nguyễn Lê Phước Thịnh CTV 
21 tháng 8 2021 lúc 21:03 a: Ta có: \(a+b+c=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
Ta có: a+b+c=0
\(\Leftrightarrow\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
b: Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Leftrightarrow a+b+c=0\)
Đúng 3 Bình luận (0) Gửi Hủy 
Lấp La Lấp Lánh 
21 tháng 8 2021 lúc 21:14 a) \(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)(đúng do a+b+c = 0)
Đúng 1 Bình luận (0) Gửi Hủy Lấp La Lấp Lánh 21 tháng 8 2021 lúc 21:21 b) Ta có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\\left(b-c\right)^2\ge0\\\left(c-a\right)^2\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a^2+b^2\ge2ab\\b^2+c^2\ge2bc\\c^2+a^2\ge2ac\end{matrix}\right.\Rightarrow a^2+b^2+c^2\ge ab+ac+bc\)
\(ĐTXR\Leftrightarrow a=b=c\), mà a,b,c đôi một khác nhau => Đẳng thức không xảy ra\(\Rightarrow a^2+b^2+c^2>ab+ac+bc\Rightarrow a^2+b^2+c^2-ab-ac-bc>0\)
Ta có: \(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)\(\Rightarrow a+b+c=0\)( do (1))
Đúng 1 Bình luận (0) Gửi Hủy - Lelemalin
Bài 1:
a) Cho a + b + c = 0. CMR: a3 + b3+ c3 = 3abc
b) Cho a3 + b3 + c3 = 3abc và a. b, c đôi một khác nhau. CMR: a + b + c = 0
Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 21 tháng 8 2021 lúc 21:29 a: Ta có: a+b+c=0
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
Ta có: a+b+c=0
\(\Leftrightarrow\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
b: Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)
\(\Leftrightarrow a+b+c=0\)
Đúng 2 Bình luận (0) Gửi Hủy 
- Hoàng Hưng Đạo
2. Chứng minh rằng:
a. a3+ b3 = (a + b)3 - 3ab (a + b)
b. a3+ b3 + c3 - 3abc = (a + b + c) (a2 + b2 c2 - ab - bc - ca)
Xem chi tiết Lớp 8 Toán 2 0 Gửi Hủy 
zanggshangg 
14 tháng 5 2021 lúc 21:04 a )
`VP= (a+b)^3-3ab(a+b)`
`=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2`
`=a^3+b^3 =VT (đpcm)`
b)
b) Ta có
`VT=a3+b3+c3−3abc`
`=(a+b)3−3ab(a+b)+c3−3abc`
`=[(a+b)3+c3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)2+c2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a2+b2+2ab+c2−ac−bc−3ab)`
`=(a+b+c)(a2+b2+c2−ab−bc−ca)=VP`
Đúng 0 Bình luận (0) Gửi Hủy zanggshangg 14 tháng 5 2021 lúc 21:09
a) Ta có:
`VP= (a+b)^3-3ab(a+b)`
`=a^3 + b^3+3ab ( a + b )- 3ab ( a + b )`
`=a^3 + b^3=VT(dpcm)`
b) Ta có
`VT=a^3+b^3+c^3−3abc`
`=(a+b)^3−3ab(a+b)+c^3−3abc`
`=[(a+b)^3+c^3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)^2+c^2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a^2+b^2+2ab+c^2−ac−bc−3ab)`
`=(a+b+c)(a^2+b^2+c^2−ab−bc−ca)=VP`
Đúng 0 Bình luận (0) Gửi Hủy 
- Nguyễn Ngọc Anh
Cho a+b+c+d=0. CMR: a3+b3+c3+d3=3(c+d)(ab-cd)
Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 3 0 Gửi Hủy 
Lê Song Phương 
5 tháng 8 2023 lúc 6:42 Ta có:
\(a^3+b^3+c^3+d^3\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+\left(c+d\right)^3-3cd\left(c+d\right)\)
\(=-\left(c+d\right)^3+3ab\left(c+d\right)+\left(c+d\right)^3-3cd\left(c+d\right)\) (vì \(a+b=-\left(c+d\right)\))
\(=3\left(c+d\right)\left(ab-cd\right)\)
Vậy đẳng thức được chứng minh.
Đúng 1 Bình luận (0) Gửi Hủy 
Đặng Ninh Phượng 4 tháng 8 2023 lúc 22:36 ...
Đúng 0 Bình luận (0) Gửi Hủy 
Đào Trí Bình 
5 tháng 8 2023 lúc 6:42 lần sau nhé
Đúng 0 Bình luận (0) Gửi Hủy 
- Đào Thu Hiền
-
1) Cho a, b, c ∈ [0;1] và a + b + c = 2. CMR ab + bc + ca ≥ 2abc + \(\dfrac{20}{27}\)
2) Cho a, b, c ∈ [1;3] và a + b + c = 6. CMR a3 + b3 + c3 ≤ 36
3) Cho các số dương a, b, c, d thoả mãn a + b + c + d = 4. CMR \(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+d^2}+\dfrac{d}{1+a^2}\) ≥ 2
Xem chi tiết Lớp 10 Toán 3 0 Gửi Hủy 
Rin Huỳnh 
11 tháng 2 2022 lúc 23:41 3)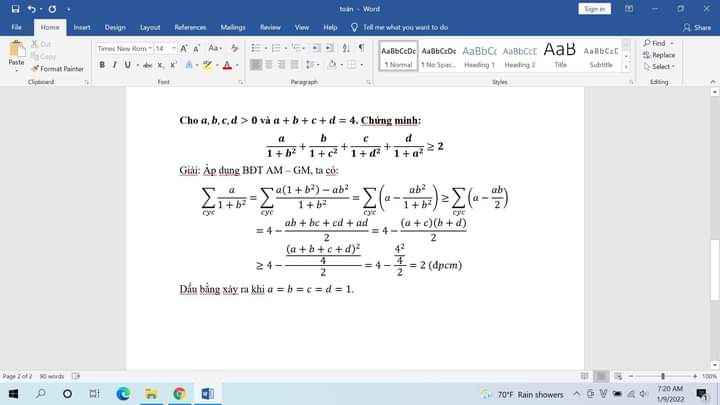
Gửi Hủy Nguyễn Việt Lâm CTV 13 tháng 2 2022 lúc 17:04 1.
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với \(\dfrac{2}{3}\), không mất tính tổng quát, giả sử đó là b và c
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\ge0\)
Mặt khác \(0\le a\le1\Rightarrow1-a\ge0\)
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\left(1-a\right)\ge0\)
\(\Leftrightarrow-abc\ge\dfrac{4a}{9}+\dfrac{2b}{3}+\dfrac{2c}{3}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}\)
\(\Leftrightarrow-abc\ge-\dfrac{2a}{9}+\dfrac{2}{3}\left(a+b+c\right)-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}=-\dfrac{2a}{9}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc+\dfrac{8}{9}\)
\(\Leftrightarrow-2abc\ge-\dfrac{4a}{9}-\dfrac{4ab}{3}-\dfrac{4ac}{3}-2bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{ab}{3}-\dfrac{ac}{3}-bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(b+c\right)-bc+\dfrac{16}{9}\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(2-a\right)-\dfrac{\left(b+c\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}+\dfrac{a^2}{3}-\dfrac{2a}{3}-\dfrac{\left(2-a\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge\dfrac{a^2}{12}-\dfrac{a}{9}+\dfrac{7}{9}=\dfrac{1}{12}\left(a-\dfrac{2}{3}\right)^2+\dfrac{20}{27}\ge\dfrac{20}{27}\)
\(\Rightarrow ab+bc+ca\ge2abc+\dfrac{20}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{2}{3}\)
Đúng 1 Bình luận (1) Gửi Hủy Nguyễn Việt Lâm CTV 13 tháng 2 2022 lúc 17:04 2.
Đặt \(\left(a;b;c\right)=\left(x+1;y+1;z+1\right)\Rightarrow\left\{{}\begin{matrix}x;y;z\in\left[0;2\right]\\x+y+z=3\end{matrix}\right.\)
Ta có: \(P=\left(x+1\right)^3+\left(y+1\right)^3+\left(z+1\right)^3\)
\(P=x^3+y^3+z^3+3\left(x^2+y^2+z^2\right)+12\)
Không mất tính tổng quát, giả sử \(x\ge y\ge z\Rightarrow x\ge1\)
\(\Rightarrow\left\{{}\begin{matrix}y^3+z^3=\left(y+z\right)^3-3yz\left(y+z\right)\le\left(y+z\right)^3\\y^2+z^2=\left(y+z\right)^2-2yz\le\left(y+z\right)^2\end{matrix}\right.\)
\(\Rightarrow P\le x^3+\left(3-x\right)^3+3x^2+3\left(3-x\right)^2+12\)
\(\Rightarrow P\le15x^2-45x+66=15\left(x-1\right)\left(x-2\right)+36\le36\)
(Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\))
Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(2;1;0\right)\) và các hoán vị hay \(\left(a;b;c\right)=\left(1;2;3\right)\) và các hoán vị
Đúng 1 Bình luận (0) Gửi Hủy 
- Rosie
-
xét ba số thực a,b,c thỏa mãn 0 ≤ a,b,c ≤ 2 và a+b+c = 3. Tìm giá trị nhỏ nhất của biểu thức : P = a3+ b3+ c3 + \(\dfrac{\left(ab+bc+ca\right)^3+8}{ab+bc+ca}\)
Xem chi tiết Lớp 9 Toán Violympic toán 9 0 0 Gửi Hủy 
- Nguyễn Hà Quang Minh
cho a,b,c là số thức dương thỏa mãn a+b+c=1. Chứng minh
2(a3 + b3 + c3) + 3abc ≥ ab + bc + ca
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 6 tháng 4 2023 lúc 10:20 a+b+c=1; a>0; b>0; c>0
=>a>=b>=c>=0
=>a(a-c)>=b(b-c)>=0
=>a(a-b)(a-c)>=b(a-b)(b-c)
=>a(a-b)(a-c)+b(b-a)(b-c)>=0
mà (a-c)(b-c)*c>=0 và c(c-a)(c-b)>=0
nên a(a-b)(a-c)+b(b-a)(b-c)+(a-c)(b-c)*c>=0
=>a^3+b^3+c^3+3acb>=a^2b+a^2c+b^2c+b^2a+c^2b+c^2a
=>a^3+b^3+c^3+6abc>=(a+b+c)(ab+bc+ac)
=>a^3+b^3+c^3+6abc>=(ab+bc+ac)
mà a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)
nên 2(a^3+b^3+c^3)+3acb>=a^2+b^2+c^2>=ab+bc+ac(ĐPCM)
Đúng 0 Bình luận (0) Gửi Hủy 
- KIRI NITODO
+) Cho a3 + b3 + c3 = 3abc. CMR: a + b + c = 0 và a = b = c
+) Áp dụng: Cho a3 + b3 + c3 = 3abc, vào bài toán:
Tính giá trị của biểu thức P= \(\dfrac{a+b}{c}\cdot\dfrac{b+c}{a}\cdot\dfrac{c+a}{b}\)
Xem chi tiết Lớp 8 Toán Bài 5: Những hằng đẳng thức đáng nhớ (Tiếp) 1 0 Gửi Hủy 
Akai Haruma Giáo viên 29 tháng 6 2023 lúc 16:54 Bài 1:
$a^3+b^3+c^3=3abc$
$\Leftrightarrow (a+b)^3-3ab(a+b)+c^3-3abc=0$
$\Leftrightarrow [(a+b)^3+c^3]-[3ab(a+b)+3abc]=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Xét TH $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$$\Rightarrow a-b=b-c=c-a=0$
$\Leftrightarrow a=b=c$
Vậy $a^3+b^3+c^3=3abc$ khi $a+b+c=0$ hoặc $a=b=c$
Áp dụng vào bài:
Nếu $a+b+c=0$
$A=\frac{-c}{c}+\frac{-b}{b}+\frac{-a}{a}=-1+(-1)+(-1)=-3$
Nếu $a=b=c$
$P=\frac{a+a}{a}+\frac{b+b}{b}+\frac{c+c}{c}=2+2+2=6$
Đúng 3 Bình luận (0) Gửi Hủy Từ khóa » Cho A B C 0 Cmr A^3/b+b3/c+c^3/a =ab+bc+ca
-
Cho A, B, C > 0. Chứng Minh A^3/b + B^3/c + C^3/a ≥ Ab + Bc + Ac
-
Cho A,b,c >0 CMR A3/b B3/c C3/a>=ab Bc CaMong Mọi Người Giải Chi ...
-
Cho A,b,c >0 CMR A3/b+b3/c+c3/a>=ab+bc+caMong Mọi ... - Olm
-
Chứng Minh A^3/b+b^3/c+c^3/a>=ab+bc+ca - Con Cai
-
Top 13 Cho A B C 0 Cmr A^3/b+b3/c+c^3/a =ab+bc+ca - MarvelVietnam
-
Cho A,b,c>0 Chứng Minh A^3/b + B3/c + C3/a>=ab+ac+bc - Pitago.Vn
-
Cho A+b+c=0 Chứng Minh A^3+b^3+c^3=3abc
-
(DOC) 50 Bài Tập Về Bất đẳng Thức | Khôi Nguyễn
-
Toán 9 | Cộng đồng Học Sinh Việt Nam - HOCMAI Forum
-
HẰNG ĐẲNG THỨC ỨNG DỤNG - Tài Liệu Text - 123doc
-
Bộ Sưu Tập Bất đẳng Thức Của Võ Quốc Bá Cẩn - SlideShare