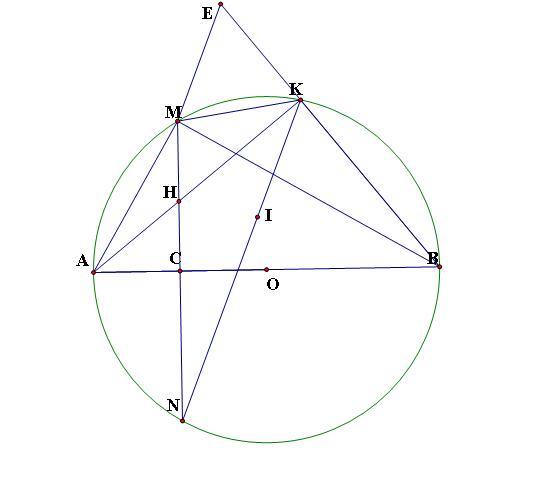
Cho đường Tròn (O) đường Kính AB = 2R, C Là Trung điểm OA Và Dây ...

Học liệu Hỏi đáp Đăng nhập Đăng ký

• Học bài
• Hỏi bài
• Kiểm tra
• ĐGNL
• Thi đấu
• Thư viện số
• Bài viết Cuộc thi Tin tức Blog học tập
• Trợ giúp
• Về OLM

(Từ ngày 12/12) Lớp live ôn thi cuối kỳ I hoàn toàn miễn phí - Tham gia ngay!!!

 Mở bộ đề mới - nhận quà VIP liền tay

• Mẫu giáo
• Lớp 1
• Lớp 2
• Lớp 3
• Lớp 4
• Lớp 5
• Lớp 6
• Lớp 7
• Lớp 8
• Lớp 9
• Lớp 10
• Lớp 11
• Lớp 12
• ĐH - CĐ

K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác nhận câu hỏi phù hợp

×

Chọn môn học Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Mua vip

• Tất cả
• Mới nhất
• Câu hỏi hay
• Chưa trả lời
• Câu hỏi vip

TL thành lê 15 tháng 3 2018 - olm

Cho đường tròn (O) đường kính AB = 2R, C là trung điểm OA và dây MN vuông góc CA tại C.  Gọi K là trung điểm tùy ý trên cung nhỏ BM,  H là giao điểm của AK và MN

a)  Cm BCHK nội tiếp

b)  Tính tích AH, AK theo R

c)  Xác định vị trí điểm K để tổng (KN + KM + KB) đạt GTLN và tính GTLN đó theo R                                  MỌI NGƯỜI GIÚP MK VỚI MK ĐANG CẦN LẮM Ạ

#Hỏi cộng đồng OLM #Toán lớp 9 1 AP anh pham 16 tháng 3 2018

Mình giải giúp câu a, b, cho bạn nhé bạn 

a, tam giác ABK có : AB là đường kính ; K thuộc (O)

suy ra góc AKB = 90 độ 

Xét tứ giác BCHK có : góc MCB + góc AKB = 90 độ + 90 độ = 180 độ 

suy ra tứ giác BCHK nội tiếp đường tròn

b, xét tam giác ACH và tam giác AKB có ;

góc A chung

góc ACH = góc AKB = 90 độ 

suy ra tam giác ACH đồng dạng với tam giác AKB (g. g)

suy ra AH/AB = AC/AK hay AH/2R = R chia 2/AK

khi và chỉ khi AH . AK = 2R . R/2 = R bình 

vậy AH.AK= R bình

Đúng(0) Các câu hỏi dưới đây có thể giống với câu hỏi trên TN Tư Ngâm 20 tháng 5 2017 - olm

Cho đường tròn (O) đường kính AB = 2R, C là trung điểm OA và dây MN vuông góc CA tại C.  Gọi K là trung điểm tùy ý trên cung nhỏ BM,  H là giao điểm của AK và MN

a)  Cm BCHK nội tiếp

b)  Tính tích AH, AK theo R

c)  Xác định vị trí điểm K để tổng (KN + KM + KB) đạt GTLN và tính GTLN đó

#Hỏi cộng đồng OLM #Toán lớp 9 0 CD Cỏ dại 9 tháng 5 2020 - olm

Cho đường tròn (O) đường kính AB = 2R, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ MB, H là giao điểm của AK với MN.

a, C/minh: Tứ giác CBHK nội tiếp 

b, Tính tích AH. AK theo R

c, C/minh: \(\Delta BMN\) là tam giác đều

d, Xác định vị trí của điểm K để KM + KN + KB đạt GTLN và tính GTLN theo R.

#Hỏi cộng đồng OLM #Toán lớp 9 0 LT Lê Tài Bảo Châu 1 tháng 11 2020 - olm Bài 1: Cho tam giác ABC nhọn ( AB<AC) nội  tiếp đường tròn (O). Gọi H là hình chiếu vuông góc của A trên BC. Gọi M và N lần lượt là hình chiếu vuông góc của B và C trên đường kính AD của đường tròn(O)a) CM tứ giác ABHM,AHNC nội tiếpb) CM tam giác HMN đồng dạng tam giác ABCc) Chứng minh HM vuông góc với ACd) Gọi I là tủng điểm của BC. CM I là tâm đường tròn ngoại tiếp tam giác HMNBài 2:Cho đường...Đọc tiếp

Bài 1: Cho tam giác ABC nhọn ( AB<AC) nội  tiếp đường tròn (O). Gọi H là hình chiếu vuông góc của A trên BC. Gọi M và N lần lượt là hình chiếu vuông góc của B và C trên đường kính AD của đường tròn(O)

a) CM tứ giác ABHM,AHNC nội tiếp

b) CM tam giác HMN đồng dạng tam giác ABC

c) Chứng minh HM vuông góc với AC

d) Gọi I là tủng điểm của BC. CM I là tâm đường tròn ngoại tiếp tam giác HMN

Bài 2:Cho đường tròn (O) đường kính AB=2R, Cl à trung điểm của OA và dây MN vuông góc với OA tại C. K là điểm di động trên cung nhỏ MB và H là giao của AK và MN

a) CM tứ giác BCHK nội tiếp

b) Chứng minh tam giác MBN đều

c) Tìm vị trí điểm K trên cung nhỏ MB sao cho KM+KN+KB đạt giá trị lớn nhất và tính giá trị lớn nhất đó theo R 

#Hỏi cộng đồng OLM #Toán lớp 9 0 NT Nguyễn Trung Kiên 3 tháng 5 2016 - olm

Cho đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm của OA; qua C kẻ đường thẳng vuông góc với OA cắt đường tròn đó tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K ( K khác B và M), trên tia KN lấy điểm I sao cho KI = KM. Gọi H là giao điểm của AK và MN. Chứng minh rằng:

1. Tứ giác BCHK là tứ giác nội tiếp.

2. AK.AH = R2

3. NI = BK

#Hỏi cộng đồng OLM #Toán lớp 9 0 0D 06-Đinh Mạnh Hòa 21 tháng 5 2023

Cho đường tròn (O) và đường kính AB =2R. Gọi C là trung điểm OA, Qua C kẻ dây MN vuông góc với AB. Trên cung nhỏ MB lấy điểm K bất kì trên tia KN lấy KI=KM. Gọi H là giao điểm AK và MN . Chứng minh:a) Tứ giác BCHK nội tiếpb) AK.AH= R2c) tam giác MBN đều

#Hỏi cộng đồng OLM #Toán lớp 9 1 NL Nguyễn Lê Phước Thịnh 21 tháng 5 2023

a: góc AKB=1/2*180=90 độ

góc HCB+góc HKB=180 độ

=>BKHC nội tiếp

b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có

góc CAH chug

=>ΔACH đồng dạng với ΔAKB

=>AC/AK=AH/AB

=>AK*AH=AC*AB=1/2R*2R=R^2

Đúng(0) BQ Bùi Quỳnh Nga 18 tháng 5 2017 - olm

Cho (O;AB=2R). Gọi Cho là trung điểm của OA; qua C kẻ đường thẳng vuông góc với OA cắt đường tròn tại 2 điểm phân biệt M và N . Trên cung nhỏ BM lấy điểm K ( K khác B và M) trên tia KN lấy điểm I sao cho KI=KM. Gọi H là giáo điểm của AK và MN. Chứng minh rằng:

1. Tứgiác BCHK nội tiếp

2.AK.AH=R^2

3. NI=BK

#Hỏi cộng đồng OLM #Toán lớp 9 2 BV Bình Vũ 16 tháng 4 2018

a.

Góc AKB là góc nội tiếp chắn nửa (O) nên ∠AKB=90o∠AKB=90o

Khi này dễ dàng có đpcm

b.

Do C là trung điểm OA nên AC=OA2=R2AC=OA2=R2

Tứ giác BCHK nội tiếp nên chứng minh được △AHC∼△ABK△AHC∼△ABK

Từ đó: ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2

c.

Lấy điểm E trên tia đối của BK sao cho KE=KM=KI

Chứng minh được tam giác AMO đều (có 3 cạnh = nhau) khi đó ∠MAB=60o∠MAB=60o

Dễ dàng chứng minh được tứ giác ABKM nội tiếp nên ∠MKE=∠MAB=60o∠MKE=∠MAB=60o

khi đó tam giác MKE đều nên ME = MK(1)

Có ∠CMB=∠MAB=6oo∠CMB=∠MAB=6oo (hai góc cùng phụ với góc AMC) nên

∠MNK=∠BME(2)∠MNK=∠BME(2)

Góc CMB=60oCMB=60o nên MB=2MCMB=2MC mà MN=2MCMN=2MC nên MN=MB(3)MN=MB(3)

Từ (1),(2) và (3) nên △NMK=△BME△NMK=△BME nên NK=BENK=BE hay NI+IK=BK+KINI+IK=BK+KI từ đó có đpcm

Hình gửi kèm

• 

Đúng(0) NP nguyễn phương thảo 25 tháng 7 2020

cần gắp ko bn êi

Đúng(0) Xem thêm câu trả lời CH Cô Hoàng Huyền Admin VIP 22 tháng 3 2021 - olm

Cho đường tròn tâm $O$ đường kính $AB = 2R$. Gọi $C$ là trung điểm của $OA$; qua $C$ kẻ đường thẳng vuông góc với $OA$ cắt đường tròn đó tại hai điểm phân biệt $M$ và $N$. Trên cung nhỏ $BM$ lấy điểm $K$ ($K$ khác $B$ và $M$). Gọi $H$ là giao điểm của $AK$ và $MN$. Chứng minh rằng tứ giác $BCHK$ là tứ giác nội tiếp.     

#Hỏi cộng đồng OLM #Toán lớp 9 2 PD Phạm Đoan Trang 14 tháng 5 2021

   Ta có: góc AKP = 90độ ( Góc nội tiếp chắn nửa đường tròn)

Mà AK giao MN tại H =) Góc HKP = 90độ (1)

  Lại có: MC vuông góc AB =) Góc HCB = 90độ (2)

Từ (1) và (2) =) góc HKP + góc HCP = 180độ

Mà 2 góc đối nhau

=) Tứ giác BCHK nội tiếp

Đúng(1) NT Nguyễn Thế Hải 14 tháng 5 2021

Đúng(0) Xem thêm câu trả lời NA Ngọc Anh 2 tháng 12 2016 - olm Cho AB là đường kính của đường tròn (O;R). C là một điểm thay đổi trên đường tròn ( C khác A và B), CH vuông góc với AB tại H. gọi I là trung điểm của AC, OI cắt tiếp tuyến tại A của đường tròn (O;R) tại M, MB cắt CH tại K.a) CMR: 4 điểm C,H,O,I thuộc cùng một đường trònb) CMR: K là trung điểm của CHc) Xác định vị trí của C để chu vi tam giác ACB đạt GTLN? tìm GTLN đó theo R****Mấy bạn...Đọc tiếp

Cho AB là đường kính của đường tròn (O;R). C là một điểm thay đổi trên đường tròn ( C khác A và B), CH vuông góc với AB tại H. gọi I là trung điểm của AC, OI cắt tiếp tuyến tại A của đường tròn (O;R) tại M, MB cắt CH tại K.

a) CMR: 4 điểm C,H,O,I thuộc cùng một đường tròn

b) CMR: K là trung điểm của CH

c) Xác định vị trí của C để chu vi tam giác ACB đạt GTLN? tìm GTLN đó theo R

****Mấy bạn giúp mk với ạ! *)) Mơn!!

#Hỏi cộng đồng OLM #Toán lớp 9 0 MM Măm Măm 9 tháng 5 2020

Cho đường tròn (O) đường kính AB = 2R, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ MB, H là giao điểm của AK với MN.

a, C/minh: Tứ giác CBHK nội tiếp

b, Tính tích AH. AK theo R

c, C/minh: \(\Delta BMN\) là tam giác đều

d, Xác định vị trí của điểm K để KM + KN + KB đạt GTLN và tính GTLN theo R.

#Hỏi cộng đồng OLM #Toán lớp 9 1 A 💋Amanda💋 9 tháng 5 2020 https://i.imgur.com/F1RGKY5.jpg Đúng(0) Xếp hạng Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên

• Tuần
• Tháng
• Năm

• -❇️🆗𝕰𝔛𝕻𝔈𝕽ℑ𝕰𝔑𝕮𝔈𝕯✳️𝕻𝔈𝕺𝔓𝕷𝔈🆒❎- 25 GP
• ︻デ═一👑𝓚𝓐𝓞𝓡𝓤 𝓜𝓘𝓣𝓞𝓜𝓐👑𝓕𝓕一═デ︻ 12 GP
• SV Sinh Viên NEU 12 GP
• NV ✫⊰ Ngô Vũ ༒ Công Vinh ⊱✫ VIP 10 GP
• E ElmSunn(2012) 6 GP
• NT Nguyễn Thị Thiên Ái 6 GP
• B bothaybuonvl :(😶😑😐😕🙁😟😞😖😦😧😢😰😨😱🥶🥴🤯 6 GP
• VP Vũ Phương Thanh 4 GP
• FC FA Cệ Bố Ok 4 GP
• NS Nguyễn Sỹ Quang 4 GP

Học liệu Hỏi đáp Link rút gọn Link rút gọn Để sau Đăng ký

Các khóa học có thể bạn quan tâm

× Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

×

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.