Cho Hàm Số \(y = F\left( X \right)\). Đồ Thị Hàm Số ...

Câu hỏi số 438382: Vận dụng

Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ.

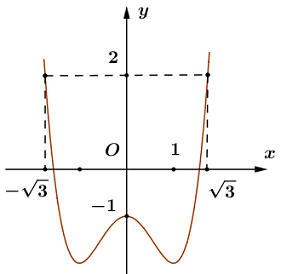
Đặt \(h\left( x \right) = 3f\left( x \right) - {x^3} + 3x\). Tìm mệnh đề đúng trong các mệnh đề sau:

A. \(\mathop {\max }\limits_{\left[ { - \sqrt 3 ;\sqrt 3 } \right]} h\left( x \right) = 3f\left( 1 \right)\) B. \(\mathop {\max }\limits_{\left[ { - \sqrt 3 ;\sqrt 3 } \right]} h\left( x \right) = 3f\left( { - \sqrt 3 } \right)\) C. \(\mathop {\max }\limits_{\left[ { - \sqrt 3 ;\sqrt 3 } \right]} h\left( x \right) = 3f\left( {\sqrt 3 } \right)\) D. \(\mathop {\max }\limits_{\left[ { - \sqrt 3 ;\sqrt 3 } \right]} h\left( x \right) = 3f\left( 0 \right)\)

Đáp án đúng là: B

Quảng cáo

Xem lời giải Câu hỏi:438382 Phương pháp giải

- Tính \(h'\left( x \right)\), giải phương trình \(h'\left( x \right) = 0\) bằng phương pháp tương giao đồ thị.

- Dựa vào đồ thị xác định tính đơn điệu của hàm số \(h\left( x \right)\) trên \(\left[ { - \sqrt 3 ;\sqrt 3 } \right]\), từ đó suy ra \(\mathop {Max\,h\left( x \right)}\limits_{x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]} \).

Giải chi tiết

+ \(h'\left( x \right) = 3f'\left( x \right) - 3{x^2} + 3 = 3\left[ {f'\left( x \right) - \left( {{x^2} - 1} \right)} \right]\)

+ \(h'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} - 1\,\,\left( * \right)\)

Giải PT \(\left( * \right)\) bằng cách vẽ tương giao đồ thị \(f'\left( x \right)\) và \(Parabol\,\,\left( P \right):y = {x^2} - 1\)

Vẽ \(\left( P \right)\)

         + Trục đứng: \(x = \dfrac{{ - b}}{{2a}} = 0\)

         + Đỉnh \(\left( P \right):\left( {0; - 1} \right)\)

                        + Điểm \(\left( P \right)\) đi qua: \(\left( { - \sqrt 3 ;2} \right);\left( {\sqrt 3 ;2} \right)\)

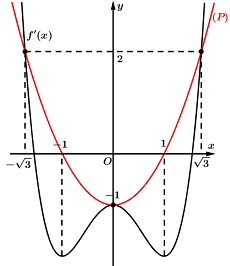
+ Quan sát đồ thị \(f'\left( x \right)\) và \(\left( P \right)\)

     \( \Rightarrow \)Khi \(x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\) thì đồ thị \(\left( P \right)\) luôn nằm trên \(f'\left( x \right)\)

     \(\begin{array}{l} \Rightarrow f'\left( x \right) - \left( {{x^2} - 1} \right) \le 0,\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\\ \Rightarrow h'\left( x \right) \le 0,\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\end{array}\)

     \( \Rightarrow \) Hàm số \(h\left( x \right)\) nghịch biến trên \(\left[ { - \sqrt 3 ;\sqrt 3 } \right]\)

     \( \Rightarrow \mathop {Max\,h\left( x \right)}\limits_{x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]}  = h\left( { - \sqrt 3 } \right) = 3f\left( { - \sqrt 3 } \right)\)

Chọn B.

Đáp án cần chọn là: B