Cho Hàm Số Y = F( X ). Đồ Thị Hàm Số Y = F'( X ) Như Hình Vẽ. Đặt G( X ...

Có thể bạn quan tâm

LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY XEM CHI TIẾT

Cho hàm số y = f( x ). Đồ thị hàm số y = f'( x ) như hình vẽ. Đặt g( x ) = 3f( x ) - x^3 + 3x - m vớ

Câu hỏi

Nhận biết

Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = 3f\left( x \right) - {x^3} + 3x - m\), với \(m\) là tham số thực. Điều kiện cần và đủ để bất phương trình \(g\left( x \right) \ge 0\) nghiệm đúng với \(\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\) là

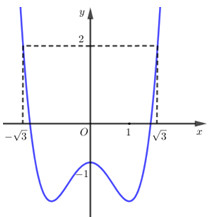
A. \(m \le 3f\left( {\sqrt 3 } \right)\) B. \(m \le 3f\left( 0 \right)\) C. \(m \ge 3f\left( 1 \right)\) D. \(m \ge 3f\left( { - \sqrt 3 } \right)\)

Đáp án đúng: A

Lời giải của Tự Học 365

Giải chi tiết:

Ta có: \(g\left( x \right) = 3f\left( x \right) - {x^3} + 3x - m \ge 0 \Leftrightarrow 3f\left( x \right) - {x^3} + 3x \ge m\)

Điều kiện bài toán trở thành tìm \(m\) để \(3f\left( x \right) - {x^3} + 3x \ge m,\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\).

Xét hàm \(h\left( x \right) = 3f\left( x \right) - {x^3} + 3x\) trên đoạn \(\left[ { - \sqrt 3 ;\sqrt 3 } \right]\) ta có:

\(h'\left( x \right) = 3f'\left( x \right) - 3{x^2} + 3 = 3\left( {f'\left( x \right) - {x^2} + 1} \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} - 1\)

Dựng đồ thị hàm số \(y = {x^2} - 1\) cùng một hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\) bài cho ta được:

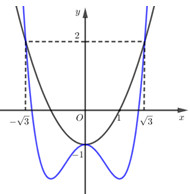
Xét trên đoạn \(\left( { - \sqrt 3 ;\sqrt 3 } \right)\) thì \(f'\left( x \right) \le {x^2} - 1,\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\).

Do đó \(f'\left( x \right) - {x^2} + 1 \le 0,\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\) hay hàm số \(y = h\left( x \right)\) nghịch biến trên \(\left[ { - \sqrt 3 ;\sqrt 3 } \right]\).

Suy ra \(h\left( { - \sqrt 3 } \right) \ge h\left( x \right) \ge h\left( {\sqrt 3 } \right)\,\,\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\) hay \(3f\left( { - \sqrt 3 } \right) \le h\left( x \right) \le 3f\left( {\sqrt 3 } \right)\).

Điều kiện bài toán thỏa \( \Leftrightarrow m \le \mathop {\min }\limits_{\left[ { - \sqrt 3 ;\sqrt 3 } \right]} h\left( x \right) = h\left( {\sqrt 3 } \right) = 3f\left( {\sqrt 3 } \right)\).

Vậy \(m \le 3f\left( {\sqrt 3 } \right)\).

Chọn A.

Ý kiến của bạn Hủy

Luyện tập

Phòng tự luyện, thi thử
Khóa học, tài liệu
Cách tự học

Câu hỏi liên quan

Tìm số nguyên dương n nhỏ nhất sao cho z1 = là số thực và z2 = là số ảo.
Chi tiết
Giải phương trình: (sin2x + cos2x)cosx + 2cos2x - sinx = 0
Chi tiết
câu 2

Chi tiết
Giải phương trình 72x + 1 – 8.7x + 1 = 0.
Chi tiết
Giải phương trình 31 – x – 3x + 2 = 0.
Chi tiết
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d: = = và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
Chi tiết
Câu 2: Đề thi thử THPT Hà Trung - Thanh Hóa

Chi tiết
Giải phương trình : z3 + i = 0
Chi tiết
Giải phương trình (1 – i)z + (2 – i) = 4 – 5i trên tập số phức.
Chi tiết
câu 7

Chi tiết