Cho Số Phức Z= (1-i)/(1+i). Phần Thực Của Số Phức Z ...

× Đăng nhập Facebook Google ×

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Quảng cáo

Trang chủ Lớp 12 Toán

Câu hỏi:

22/07/2024 2,446

Cho số phức z= 1-i1+i.Phần thực của số phức z2017 là

Quảng cáo

A. 0

Đáp án chính xác

B. 1

C. 2

D. 3

Xem lời giải Xem lý thuyết Câu hỏi trong đề: Bài tập Số phức cực hay có lời giải chi tiết Bắt Đầu Thi Thử

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án A

Ta có: z = 1-i1+i=1-i21-i2=-i

Do đó z2017=-i2017=-i.-i2016=-i.-i21008=-i

Vậy phần thực của số phức z2017 là 0.

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

Quảng cáo

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho i là đơn vị ảo. Giá trị của biểu thức z = i5+i4+i3+i2+i+140là

Xem đáp án » 12/03/2022 4,468

Câu 2:

Gọi z1, z2 là các nghiệm của phương trình z2 -2z + 6 = 0. Tính P = z14  + z24

Xem đáp án » 12/03/2022 3,857

Câu 3:

Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn |z - i + 1| = |z + i - 2|là đường thẳng có phương trình

Xem đáp án » 12/03/2022 1,829

Câu 4:

Cho i là đơn vị ảo. Với x,y∈ℝthì x - 1 + (y + 3)i là số thuần ảo khi và chỉ khi

Xem đáp án » 12/03/2022 1,474

Câu 5:

Cho số phức z = a+bi ; a,b ∈ℝ.Nhận xét nào sau đây luôn đúng?

Xem đáp án » 12/03/2022 1,233

Câu 6:

Cho i là đơn vị ảo. Cho m∈ℝ. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn hình học số phức z = micó tọa độ là

Xem đáp án » 12/03/2022 969

Câu 7:

Phần thực của số phức w= 1+ 1+i+1+i2+1+i3+...+1+i1999 bằng

Xem đáp án » 12/03/2022 809

Câu 8:

Cho số phức z thỏa mãn điều kiện z +1i-z¯là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng

Xem đáp án » 12/03/2022 713

Câu 9:

Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn z-1-i=1. Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng ?

Xem đáp án » 12/03/2022 596

Câu 10:

Số phức z thỏa mãn (2 + 3i)z + 1-iz = 3+5iTìm môđun của số phức z.

Xem đáp án » 12/03/2022 583

Câu 11:

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z +1 ≤2là

Xem đáp án » 12/03/2022 562

Câu 12:

Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện zi-1-2i=4 là

Xem đáp án » 12/03/2022 562

Câu 13:

Số phức liên hợp của số phức z = 1+i4-3ilà

Xem đáp án » 12/03/2022 527

Câu 14:

Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức -2, 4i, x+2i. Với giá trị nào của x thì A, B, M thẳng hàng.

Xem đáp án » 12/03/2022 420

Câu 15:

Cho z = 1 + 2i, số phức z,đối xứng với số phức z qua gốc tọa độ O (0;0)là

Xem đáp án » 12/03/2022 384 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

1. Số i.

Số i là số thỏa mãn: i2 = –1.

2. Định nghĩa số phức

Mỗi biểu thức dạng a + bi , trong đó a;b∈R; i2 = –1 được gọi là một số phức.

Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.

Tập hợp các số phức kí hiệu là C.

Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i; 5-i⁢2;3+2⁢i.

Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.

3.Số phức bằng nhau

– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :

a + bi = c + di ⇔ a = c và b = d.

Ví dụ 3. Tìm các số thực x và y biết :

(2x – 1) + (y – 2)i = 3 + (4 – y)i

Lời giải:

Ta có : (2x – 1) + (y – 2)i = 3 + (4 – y)i

⇔{2x-1= 3y-2=  4-y⇔{x=2y= 3.

Vậy x = 2 và y = 3.

– Chú ý :

a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.

Như vậy, mỗi số thực cũng là một số phức. Ta có : R⊂⁢C.

b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi

Đặc biệt : i = 0 + 1.i

Số i được gọi là đơn vị ảo.

Ví dụ 4. Số phức z có phần thực là -12 và phần ảo là 12 là z=-12+12⁢i.

4. Biểu diễn hình học số phức

Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.

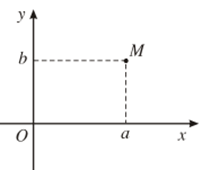
Ví dụ 5.

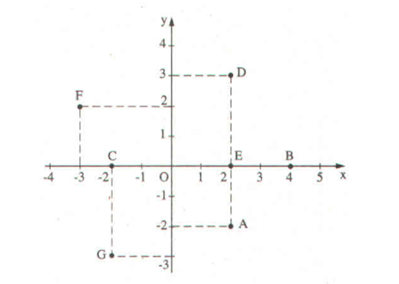
Điểm A biểu diễn số phức 2 – 2i

Điểm B biểu diễn số phức 4.

Điểm C biểu diễn số phức – 2.

Điểm D biểu diễn số phức 2 + 3i.

Điểm E biểu diễn số phức 2.

Điểm F biểu diễn số phức – 3 + 2i.

Điểm G biểu diễn số phức –2 – 3i.

5. Mô đun của số phức.

Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.

Độ dài của vecto O⁢M→ được gọi là môđun của số phức z và kí hiệu là |z|.

Vậy |z|=|O⁢M→| hay |a+b⁢i|=|O⁢M→|.

Ta thấy :|a+b⁢i|=a2+b2.

Ví dụ 6.

|-2+ 3⁢i|=(-2)2+  32=13|2-4⁢i|=(2)2+(-4)2=18

6. Số phức liên hợp

– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là z¯=a-b⁢i.

Ví dụ 7.

Nếu z = – 3 + 5i thì z¯=-3-  5⁢i.

Nếu z = – 4 + 4i thì z¯=-4-4⁢i.

– Nhận xét :

+ Trênmặt phẳng tọa độ các điểm biểu diễn z và z¯ đối xứng nhau qua trục Ox.

+ Từ định nghĩa ta có: z¯¯=z;|z¯|=|z|.

Hỏi bài

Đề thi liên quan

Xem thêm »

• 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số 10 đề 9204 lượt thi Thi thử
• Bài tập về Tính đơn điệu của hàm số có lời giải 3 đề 7754 lượt thi Thi thử
• Trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao 11 đề 7435 lượt thi Thi thử
• Bài tập tắc nghiệm ứng dụng đạo hàm - Toán 12 có đáp án 7 đề 6031 lượt thi Thi thử
• 150 câu trắc nghiệm Nguyên hàm - Tích phân cơ bản (có đáp án) 6 đề 5080 lượt thi Thi thử
• 200 câu trắc nghiệm Phương pháp tọa độ trong không gian NC (có đáp án) 9 đề 4730 lượt thi Thi thử
• Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải 5 đề 4387 lượt thi Thi thử
• 70 câu trắc nghiệm Khối đa diện cơ bản 6 đề 3899 lượt thi Thi thử
• Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án 3 đề 3851 lượt thi Thi thử
• 200 câu trắc nghiệm Phương pháp tọa độ trong không gian (có đáp án) 6 đề 3841 lượt thi Thi thử

Xem thêm »