Cho Tích Phân Của Xtan^2xdx = Api^2+bpi+c Cân Từ 0 đến Pi/4 Với A ...

Có thể bạn quan tâm

Tìm×

Tìm kiếm với hình ảnh

Vui lòng chỉ chọn một câu hỏi

Tìm đáp án

- Đăng nhập
- |
- Đăng ký

Hoidap247.com Nhanh chóng, chính xác

Hãy đăng nhập hoặc tạo tài khoản miễn phí!

Đăng nhậpĐăng ký

Đặt câu hỏi

logo

Lưu vào

+
Danh mục mới

Lưu

thaofirely
Chưa có nhóm

Trả lời
1
Điểm
80
Cảm ơn
1

Toán Học
Lớp 12
10 điểm
thaofirely - 22:30:53 17/01/2020

Cho tích phân của xtan^2xdx = api^2+bpi+c cân từ 0 đến pi/4 với a, b, c thuộc Q. Tính T = a+2b+3c? A. T = -33/32 B. T = -31/32 C. T = 25/32 D. T = 21/32 Một dạng toán của tích phân ạ

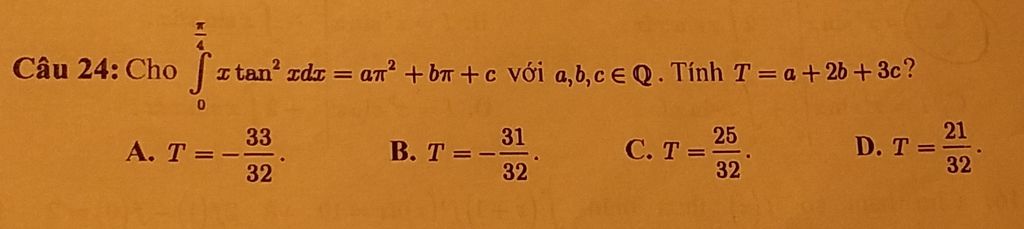
Hỏi chi tiết
Báo vi phạm

Hãy luôn nhớ cảm ơn và vote 5* nếu câu trả lời hữu ích nhé!

TRẢ LỜI

dangphuong028
Chưa có nhóm

Trả lời
14863
Điểm
166984
Cảm ơn
7718

dangphuong028

Đây là một chuyên gia không còn hoạt động

18/01/2020

Đáp án:

Giải thích các bước giải:

Đặt:

$\begin{array}{l}\begin{array}{*{20}{c}}u& = &x& \Rightarrow &{du}& = &{dx}\\{dv}& = &{({{\tan }^2}x + 1 - 1)dx}& \Rightarrow &v& = &{\tan x - x}\end{array}\\I = x(\tan x - x) - \smallint \tan x.dx + \smallint x.dx = x.\tan x - \frac{{{x^2}}}{2} - J\\J = \smallint \tan x.dx = \smallint \frac{{\sin x}}{{\cos x}}dx = - \smallint \frac{{d(\cos x)}}{{\cos x}} = - \ln |\cos x|\\ \to I = x.\tan x - \frac{{{x^2}}}{2} + \ln |\cos x| + C\\ \to \int\limits_0^{\frac{\pi }{4}} {x.{{\tan }^2}xdx = } x.\tan x\left| {_0^{\frac{\pi }{4}}} \right. - \frac{{{x^2}}}{2}\left| {_0^{\frac{\pi }{4}}} \right. + \ln |\cos x|\left| {_0^{\frac{\pi }{4}}} \right.\\ = \frac{\pi }{4} - \frac{{{\pi ^2}}}{{32}} + \ln \frac{{\sqrt 2 }}{2}\end{array}$

Hãy giúp mọi người biết câu trả lời này thế nào?

starstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarGửiHủy

Cảm ơn
Báo vi phạm

Đăng nhập để hỏi chi tiết avatar

letruonhuy
Chưa có nhóm

Trả lời
7
Điểm
136
Cảm ơn
6

letruonhuy

11/03/2020

$\begin{array}{l} \begin{matrix} u & = & x & \Rightarrow & d u & = & d x \\ d v & = & (\tan^{2} x + 1 - 1) d x & \Rightarrow & v & = & \tan x - x \end{matrix} \\ I = x (\tan x - x) - \int \tan x . d x + \int x . d x = x . \tan x - \frac{x^{2}}{2} - J \\ J = \int \tan x . d x = \int \frac{\sin x}{\cos x} d x = - \int \frac{d (\cos x)}{\cos x} = - \ln | \cos x | \\ \to I = x . \tan x - \frac{x^{2}}{2} + \ln | \cos x | + C \\ \to \int_{0}^{\frac{π}{4}} x . \tan^{2} x d x = x . \tan x |_{0}^{\frac{π}{4}} - \frac{x^{2}}{2} |_{0}^{\frac{π}{4}} + \ln | \cos x | |_{0}^{\frac{π}{4}} \\ = \frac{π}{4} - \frac{π^{2}}{32} + \ln \frac{\sqrt{2}}{2} \end{array}$