Chứng Minh đẳng Thức Vecto, Phân Tích Vecto Và Bài Tập - TÀI LIỆU RẺ

Tóm tắt tài liệu

Toggle

• Chứng minh đẳng thức vecto sau
  • Bài 1
  • Bài 6
  • Bài 8
  • Bài 13
• Bài tập có lời giải chi tiết về chứng minh đẳng thức vecto
• Xem thêm video

Trong toán học sơ cấp, véc-tơ (Vector trong tiếng Anh hay trong Hán-Việt là hướng lượng) là một đoạn thẳng có hướng. Trong Hình học 10, các bạn đã biết cụ thể về các dạng Toán liên quan đến véc-tơ, và một trong những dạng vừa dễ mà lại vừa khó đó là dạng chứng minh đẳng thức véc-tơ. Chính vì lẽ đó, TAILIEURE.COM đã tổng hợp nên tài liệu chứng minh đẳng thức vecto. Trong tài liệu, các bài tập được sắp xếp từ dễ đến khó rất hài hòa với nhau khi xem,đồng thời cung cấp đầy đủ kiến thức để làm tốt hơn dạng bài này.

TẢI XUỐNG ↓

Chứng minh đẳng thức vecto sau

Bài 1

 Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:

a) AB+ DC= AC+ DB <=> AC+ CB+ DB+ BC= AC+ DB <=> AC+ DB= AC+ DB

b) AB+ BE+ CF= AE+ BF+ CD <=> AE+ ED+ BF+ FE+ CD+ DF = AE+ BF+ CD <=> AE+ BF+ CD= AE+ BF+ CD

Bài 6

Cho tam giác ABC, M là trung điểm BC, G là trọng tâm, H là trực tâm, O là tâm đường tròn ngoại tiếp. Chứng minh rằng: a) AH= 2 OM

Lời giải: *Gọi A’ là điểm đối xứng với A qua O. => Tứ giác BHCA’ là hình bình hành. => M là trung điểm HA’

*Xét tam giác AA’H có: là trung điểm của AA’ và M là trung điểm của HA’ <=>OM là đường trung bình của tam giác AA’H <=>OM // AH và OM = 1⁄2 AH <=>AH = 2OM

b) OA+ OB+ OC= OH <=>OH+ HA+ OH+ HB+ OH+ HC= OH <=>3OH+ 2 HO= OH <=>OH=OH

Bài 8

Cho tam giác ABC. Gọi M là trung điểm của BC sao cho MB = 2MC. Chứng minh : AM=1/3AB+2/3AC. (xem thêm trong  tài liệu nhé)

Bài 13

Cho hình bình hành ABCD, đặt AB= a , AD = b.Gọi I là trung điểm của CD;G là trọng tâm của tam giác BCI. Phân tích BI,AG theo a,b. ( Xem thêm trong tài liệu )

Bài 18 : Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI . Gọi F là điểm trên cạnh BC kéo dài sao cho 5FB= 2FC.Tính AI, AFtheo AB,AC. (Xem thêm)

Bài tập có lời giải chi tiết về chứng minh đẳng thức vecto

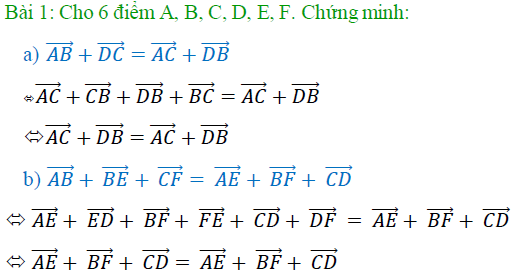
Như thế là chúng ta đã cùng đọc xong tài liệu về cách chứng minh đẳng thức vecto, cũng nắm được phần nào kiến thức về Hình học cơ bản lớp 10. Tuy rằng những bài tập trong tài liệu không khó, nhưng nó tính chọn lọc cao và có tính đặc trưng về dạng bài rất phù hợp với chương trình Hình học lớp 10. Thật tuyệt vời phải không nào?  Để học tốt phần vecto này, admin có vài kinh nghiệm nhưng trọng yếu là học “cách nhìn”. Nhìn thế nào? Đó là quan sát các cạnh xung quanh của vecto đó, và luyện nhìn luyện nhớ các bài khác nữa, nếu làm như vậy, trong một ngày thôi, khả năng làm bài vecto của các bạn sẽ nâng cao. Chúc các bạn học thật tốt nhé!

Xem thêm video