Chuỗi Fourier | Maths 4 Physics & More...
Có thể bạn quan tâm
Maths 4 Physics & more…
Blog Toán Cao Cấp (M4Ps)Tìm
Search for: Đi- Author
- Bài viết
- Bài giảng
- Giải tích 1
- Hàm số – Hàm lượng giác ngược – Hàm hyperbol
- Chia một đa thức cho tam thức bậc 2
- Giới hạn của hàm số (Limit of a function)
- Vô cùng bé (infinitesimal)
- Đạo hàm và vi phân của hàm số (derivative and differential of a function)
- Khai triển Taylor – Maclaurin (Taylor expansion)
- Khảo sát đường cong tham số
- Tích phân hữu tỷ (integration by partial fractions)
- Tích phân hàm vô tỉ (Integrals involving roots)
- Tích phân suy rộng (Improper Integrals)
- Chuỗi số. Tổng của chuỗi (Series. The total sum of series)
- Chuỗi số dương (Infinitive Series)
- Chuỗi Fourier
- Chuỗi Fourier Sine và Cosine
- Giải tích 2
- Khái niệm mở đầu về hàm nhiều biến
- Giới hạn của hàm hai biến số
- Đạo hàm riêng
- Hàm số khả vi và vi phân toàn phần
- Đạo hàm của hàm hợp
- Đạo hàm hàm số ẩn
- Cực trị (không điều kiện) của hàm 2 biến
- Cực trị có điều kiện (cực trị ràng buộc)
- Các khái niệm cơ bản của phương trình vi phân
- Phương trình tách biến, phương trình đẳng cấp cấp 1
- Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti
- Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation)
- Ứng dụng chuỗi số giải phương trình vi phân
- Tích phân hai lớp (Tích phân kép)
- Tích phân hai lớp trong tọa độ cực. Công thức đổi biến
- Tích phân đường theo tọa độ (Tp đường loại 2)
- Số phức (Complex Number)
- Đại số tuyến tính (Linear Algebra)
- Tập hợp
- Khái niệm về ma trận
- Ma trận bậc thang (Echelon matrix)
- Ma trận nghịch đảo (khả nghịch)
- Thuật toán tìm ma trận bậc thang
- Định thức (Determinants)
- Hệ phương trình tuyến tính (System of Linear Equations)
- Khái niệm về ánh xạ tuyến tính
- Không gian vectơ Euclide (Euclidean Vector Spaces)
- Trị riêng, vectơ riêng của ma trận (Eigenvalues and Eigenvectors)
- Dạng toàn phương
- Xác suất thống kê
- Bổ túc về Giải tích Tổ hợp
- Biến cố và quan hệ giữa các biến cố
- Các định nghĩa của xác suất
- Xác suất có điều kiện
- Đại lượng ngẫu nhiên 1 chiều
- Một số quy luật phân phối xác suất rời rạc
- Ước lượng tham số của tổng thể
- Kiểm định giả thiết
- Phương pháp Toán Lý (PT Đạo hàm riêng và PBĐ Laplace)
- Phép biến đổi Laplace – Các khái niệm mở đầu
- Giải tích 1
- Bài tập
- Trắc nghiệm
- Thảo luận
- Thảo luận (tiếp theo)
- Thảo luận chung (tt)
- Thảo luận về giải tích
- Thảo luận Giải tích – Trang 2
- Thảo luận ĐSTT
- Trang 2
- Trang 3
- Thảo luận XSTK
- Trang 2
- Thảo luận về tích phân bội
- Đề thi
- Ebooks
- Maths Ebooks
- Giải tích – Đại số
- XSTK – Phương pháp tính
- Hàm phức – PDEs
- Tài liệu khác
- Giáo dục – Khoa học
- Thư giãn
- Maths Ebooks
- Một thời để nhớ
- Softwares
- Links
- Sitemap
1. Các kết quả:
Biểu thức Toán học:
(1)
được gọi là chuỗi Fourier nếu (1) hội tụ.
1.1 Định nghĩa. Một đa thức Fourier là biểu thức có dạng:
Các hệ số a0, ai và bi, i = 1,2,…, n, được gọi là hệ số của Fn(x).
Đa thức Fourier là hàm tuần hoàn với chu kỳ 2π. Sử dụng các công thức lượng giác cơ bản ta có:

Chúng ta có thể chứng minh dễ dàng các công thức sau: (1) Với n ≥ 0, ta có:
và
(2) Với mọi m , n ta có:
(3) Với n ≠ m, ta có:
và
(4) Với n ≥ 1, ta có:
và
Sử dụng các công thức trên, chúng ta có kết quả sau:
1.2 Định lý: Cho
Ta có:

Định lý trên giúp ta có thể tìm được hệ số Fourier của các hàm tuần hoàn với chu kỳ T = 2π.
2. Khai triển hàm số thành chuỗi Fourier:
Định nghĩa. Cho f(x) là hàm tuần hoàn với chu kỳ T = 2π và khả tích trên đoạn [- π ; π]. Đặt:

Khi đó, chuỗi lượng giác:
được gọi là khai triển Fourier của hàm số f(x) tương ứng. Ký hiệu:
Đánh giá:
Chia sẻ:
- In
Trang: 1 2
Thảo luận
29 bình luận về “Chuỗi Fourier”
Bình luận về bài viết này Hủy trả lời
Translators & RSS
![]()
![]()
![]()

Đăng ký nhận tin
Bạn hãy nhập địa chỉ email của mình để đăng ký theo dõi tin tức từ blog này và nhận những bài viết mới nhất qua địa chỉ email.
Địa chỉ email:
Sign me up!
Tham gia cùng 2 793 người đăng ký khácĐôi lời
Bạn có thể theo dõi các lời bình liên quan đến lời bình của mình qua email bằng cách chọn dòng thông báo Báo cho bạn khi có người bình luận tiếp theo đề tài này bằng điện thư mỗi khi viết 1 lời bình.
Rất mong các bạn viết lời nhắn bằng tiếng việt có dấu nhé.
Để viết tiếng việt có dấu bạn dùng font chữ Unicode và bảng mã là Unicode UTF-8.
Để biết cách gõ công thức Toán học trong các lời nhắn ở trang web này, mời bạn đọc bài hướng dẫn tại đây hoặc bạn có thể xem bài hướng dẫn dùng MathType tại đây và bài tạo công thức trực tuyến tại đây

Lời nhắn mới nhất
| Dương Khánh Uyên trong Trang 2 | |
| Trần Thái An trong Trang 2 | |
| Chúc Chúc trong Xác suất có điều kiện | |
| Hoang Anh trong Khai triển Taylor – Macl… | |
| Trần Trung Đức trong Mẹo phân tích nhanh 1 phân… | |
| Nhung Duong trong Trang 2 | |
| khoi trong Khai triển Taylor – Macl… | |
| Minh pham trong Chuỗi Fourier Sine và Cos… | |
| Minh Phạm trong Chuỗi Fourier | |
| Anh Tuấn trong Cực trị (không điều kiện) của… |
Bài “hot”
- Khai triển Taylor - Maclaurin (Taylor expansion)
- Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti
- Ma trận nghịch đảo (khả nghịch)
- Cực trị có điều kiện (cực trị ràng buộc)
- Tích phân hai lớp (Tích phân kép)
- Cực trị (không điều kiện) của hàm 2 biến
- Phương trình tách biến, phương trình đẳng cấp cấp 1
- Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation)
- Chuỗi số. Tổng của chuỗi (Series. The total sum of series)
- Ma trận bậc thang (Echelon matrix)
Bài viết chuyên đề
- Bài giảng (20)
- Video bài giảng (4)
- Bài viết (192)
- Bài viết về ICT (59)
- Cảnh báo virus (1)
- giaovien.net (6)
- Mẹo Wordpress (13)
- Thủ thuật Gmail (7)
- Giáo dục (29)
- Khoa học (51)
- Thư giãn (45)
- Bài viết về ICT (59)
- Bí quyết học tập (20)
- Cuộc sống sinh viên (26)
- Hình ảnh và Tin tức (32)
- Làm theo lời Bác (9)
- Life's Art (61)
- nguyên tắc sáng tạo (27)
- Toán học (104)
- Lịch sử Toán học (13)
- Liên kết Toán học (6)
- Luyện thi Đại học (7)
- Đề thi thử (4)
- Vẻ đẹp Toán học (8)
- Đố vui (36)
Maths 4 Physics & more…
Tạo một blog miễn phí với WordPress.com.
Trang này sử dụng cookie. Tìm hiểu cách kiểm soát ở trong: Chính Sách Cookie- Theo dõi Đã theo dõi
-
 Maths 4 Physics & more... Đã có 938 người theo dõi Theo dõi ngay
Maths 4 Physics & more... Đã có 938 người theo dõi Theo dõi ngay - Đã có tài khoản WordPress.com? Đăng nhập.
-
-
-
 Maths 4 Physics & more...
Maths 4 Physics & more... - Theo dõi Đã theo dõi
- Đăng ký
- Đăng nhập
- URL rút gọn
- Báo cáo nội dung
- Xem toàn bộ bài viết
- Quản lý theo dõi
- Ẩn menu
-
Từ khóa » Chuỗi Fourier Là Gì
-
Chuỗi Fourier – Wikipedia Tiếng Việt
-
Biến đổi Fourier – Wikipedia Tiếng Việt
-
Chuỗi Fourier Là Gì? Chi Tiết Về Chuỗi Fourier Mới Nhất 2021
-
Sự Khác Biệt Giữa Fourier Series Và Fourier Transform - Khoa HọC
-
Fourier Là Gì
-
Loạt Fourier Là Gì? Xem Xong 5 Phút Hiểu Luôn. - Tintuctuyensinh
-
Chuỗi Fourier: Lịch Sử Và ảnh Hưởng Của Một Cơ Chế Toán Học đối ...
-
BIẾN ĐỔI FOURIER - TickLab
-
[PDF] Chuỗi Fourier Và Tích Phân Fourier - DANG TUAN HIEP
-
Fourier Là Gì - Tại Sao Biến Đổi Fourier Lại Quan Trọng Như Vậy
-
Chuỗi Fourier | Toán Cho Vật Lý
-
Chuỗi Fourier - Wiki Tiếng Việt - Du Học Trung Quốc
-
[PDF] Phần 1: Giải Tích Fourier
-
Định Nghĩa Fourier Series Là Gì?
Thầy giúp e khai triển fourier f(x)=x^2 x=(0;pi) và f(x)=x(pi-x) x=(0-pi)
ThíchThích
Được đăng bởi Minh Phạm | 03/07/2017, 18:25 Reply to this commentThầy giúp e 2 bài này với. Khai triển ham f(x) tuân hoàn chu ky 2pi thành chuỗi Florida. a. f(x)=sinax, -pi<x<pi, a#k b. f(x)=(pin-x)/2, 0<x<2.
ThíchThích
Được đăng bởi Khoa | 27/01/2015, 10:54 Reply to this commentkhai triển chuỗi Furie của hàm F(x)=x^2 (-pi,pi) thầy giúp em bài này với! e cảm ơn thầy nhiều!!
ThíchThích
Được đăng bởi bmthanh1181995 | 19/02/2014, 11:45 Reply to this commentkhai triển thành chuỗi fourier chu kì 2pi; f(x)=|X^3| trên [-pi;pi]; thầy hướng dẫn em cách làm bai này với!!! thầy có thể vẽ đồ thị bài này cho em được ko ạ?? em cám ơn thây!!!
ThíchThích
Được đăng bởi nho_pro | 23/05/2011, 22:03 Reply to this commentEm phá bỏ trị tuyệt đối, khi đó:![f(x) = \left\{\begin{array}{cc} -x^3 & ; [-\pi;0] \\ x^3 & ; [0; \pi] \\ \end{array} \right.](https://s0.wp.com/latex.php?latex=f%28x%29+%3D+%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bcc%7D+-x%5E3+%26+%3B+%5B-%5Cpi%3B0%5D+%5C%5C+x%5E3+%26+%3B+%5B0%3B+%5Cpi%5D+%5C%5C+%5Cend%7Barray%7D+%5Cright.+&bg=ffffff&fg=333333&s=0&c=20201002) Sau đó, ráp công thức hàm f(x) vào công thức khai triển. Ngoài ra, nếu em chú ý đến tính chất chẵn, lẻ của hàm f(x) thì em sẽ có
Sau đó, ráp công thức hàm f(x) vào công thức khai triển. Ngoài ra, nếu em chú ý đến tính chất chẵn, lẻ của hàm f(x) thì em sẽ có 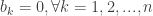
ThíchThích
Được đăng bởi 2Bo02B | 26/05/2011, 22:27 Reply to this commentE cảm ơn bài giảng của thầy. Nhờ nó mà e đã hiểu!!!!! Cảm ơn thầy rất nhiều!
ThíchThích
Được đăng bởi nguyen thi anh tuyet | 13/01/2011, 11:17 Reply to this commentHello Sir,
Thanks for uploading the Fourier Problem set. I was going through the problem set – thunhan.files.wordpress.com/2007/10/problemsfourier.pdf.
In the following problem Problem 1 (g) I think the asnwer is 2*pi.
Here is my understanding.
x(t) = 5*Cos(3*x) + 2*Cos(2*x) Fundamental Period of 5*Cos(3*x) is T1 = 2*pi/3. Fundamental Period of 2*Cos(2*x) is T2 = pi
Hence the Fundamental Period of x(t) is LCM (T1, T2) = T1*m = T2*k. where m and k are smallest possible integers so as to make LCM a integer.
(2*pi/3)*m = pi*k
Hence m is 3 and k is 2.
LCM is 2*pi.
Logically also period of 3 fundamental wave of 1st wave = period of 2 fundamentel wave of 2nd wave.
— – Harish Be exhilarated forever
ThíchThích
Được đăng bởi harish kalghatgi | 04/09/2010, 10:38 Reply to this commentThầy ơi, nếu khai triển hàm f(x) thành chuỗi Fourier trên (0, 2Pi) thì em phải làm thế nào ạ?
ThíchThích
Được đăng bởi Anh Tran | 02/11/2009, 18:13 Reply to this comment