Chương III: Bài Toán Cực Trị P điện Xoay Chiều Khi R Thay đổi
Có thể bạn quan tâm
1/ Lý thuyết toán bổ trợ vật lý: bất đẳng thức cosi: với a, b>0 a2 + b2 ≤ 2√ab2ab => (a2 + b2)min = 2ab khi a = b => (1a2+b2)(1a2+b2)max = 12ab12ab 
2/ Giá trị cực đại của P trong mạch RLC khi R thay đổi
P = I2R = U2RR2+(ZL−ZC)2U2RR2+(ZL−ZC)2 => Pmax = U2R2R|ZL−ZC|U2R2R|ZL−ZC| = U22|ZL−ZC|U22|ZL−ZC|=U22RU22R xảy ra khi Ro = |ZL – ZC|3/ R thay đổi đến giá trị R1 ≠ R2 tại đó P1 = P2 = P trong mạch RLC
P = I2R = U2RR2+(ZL−ZC)2U2RR2+(ZL−ZC)2 => R2 – U2R/P + (ZL – ZC)2 = 0 => Theo định lý viét => R1R2 = (ZL – ZC)2 = Ro2 R1 + R2 = U2/P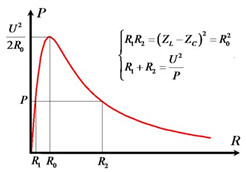
Chương III: Bài toán cực trị P điện xoay chiều khi R thay đổi
Dạng đồ thị của P theo R:
4/ Khi cuộn dây có điện trở thuần r không đổi
Pmax = U22|ZL−ZC|U22|ZL−ZC|=U22(Ro+r)U22(Ro+r) Xảy ra khi Ro + r = |ZL – ZC|Khi thay đổi R đến giá trị R1 ≠ R1 mà tại đó P1 = P2 = P
=> (R1 + r)(R2 + r) = (ZL – ZC)2 = (Ro + r)2 (R1 + r) + (R2 + r) = U2/P PR = I2R = U2R(R+r)2+(ZL−ZC)2U2R(R+r)2+(ZL−ZC)2 = U2R+r2+(ZL−ZC)2R+2rU2R+r2+(ZL−ZC)2R+2r => PR max = U22RoR+2rU22RoR+2r xảy ra khi R2 = r2 + (ZL – ZC)2Pr = I2r = U2r(R+r)2+(ZL−ZC)2U2r(R+r)2+(ZL−ZC)2
=> Pr max = U2rr2+(ZL−ZC)2U2rr2+(ZL−ZC)2 xảy ra khi R = 0Từ khóa » Cách Tính Pmax
-
Tóm Tắt Các Công Thức Về Công Suất
-
Dạng 3: Thay đổi Một Trong Các đại Lượng để Pmax
-
Bài Tập Cực Trị định Luật Ôm, Công Suất Cực đại - Vật Lí Phổ Thông
-
Thay đổi Một Trong Các đại Lượng để Pmax | 7scv
-
[Vật Lí 12] Cách Tìm Pmax | Cộng đồng Học Sinh Việt Nam
-
Công Thức Tính Công Suất - Gia Sư Tâm Tài Đức
-
Công Thức Tính Công Suất Mạch Tiêu Thụ - Chu Văn Biên - TailieuXANH
-
Tổng Hợp Các Công Thức Tính Công Suất - SPBook
-
[PDF] Cực Trị Trong Mạch điện Xoay Chiều
-
Chương II: Bài Tập định Luật Ôm, Xác định Giá Trị Cực đại - SoanBai123
-
Xác Định Giá Tối Đa (Pmax) Trên Đồ Thị | Nhật Ký Chú Cuội
-
Các Dạng Bài Tập Vật Lý 12: DẠNG 4: CÔNG SUẤT CỰC ĐẠI Pptx
-
Cách Tính Pmax Pmin,xin Giúp đỡ - Powered By Discuz! - Xaydung360
-
Bài Toán Xác định Giá Trị Cực đại Của Hiệu điện Thế Và Công Suất ...