CM Công Thức HÊ RÔNG Dùng để Tính Diện Tích Tam Giác - Hoc24

Trang chủ » Hê Rông Cho Tứ Giác » CM Công Thức HÊ RÔNG Dùng để Tính Diện Tích Tam Giác - Hoc24

Có thể bạn quan tâm

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng
  • Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Đóng Đăng nhập Đăng ký

Lớp học

  • Lớp 12
  • Lớp 11
  • Lớp 10
  • Lớp 9
  • Lớp 8
  • Lớp 7
  • Lớp 6
  • Lớp 5
  • Lớp 4
  • Lớp 3
  • Lớp 2
  • Lớp 1

Môn học

  • Toán
  • Vật lý
  • Hóa học
  • Sinh học
  • Ngữ văn
  • Tiếng anh
  • Lịch sử
  • Địa lý
  • Tin học
  • Công nghệ
  • Giáo dục công dân
  • Tiếng anh thí điểm
  • Đạo đức
  • Tự nhiên và xã hội
  • Khoa học
  • Lịch sử và Địa lý
  • Tiếng việt
  • Khoa học tự nhiên
  • Hoạt động trải nghiệm
  • Hoạt động trải nghiệm, hướng nghiệp
  • Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng
  • Lớp 10
  • Toán lớp 10

Chủ đề

  • Chương I: Mệnh đề Toán học. Tập hợp
  • Chương I: Mệnh đề và Tập hợp
  • Chương I: Mệnh đề và tập hợp
  • Chương 1: MỆNH ĐỀ, TẬP HỢP
  • Chương II: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
  • Chương II: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
  • Chương II: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
  • Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
  • Chương III: Hàm số và đồ thị
  • Chương III: Hệ thức lượng trong tam giác
  • Chương III: Hàm số bậc hai và đồ thị
  • Chương 3: PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH
  • Chương IV: Hệ thức lượng trong tam giác. Vectơ
  • Chương IV: Vectơ
  • Chương IV: Hệ thức lượng trong tam giác
  • Chương 4: BẤT ĐẲNG THỨC, BẤT PHƯƠNG TRÌNH
  • Chương V: Đại số tổ hợp
  • Chương V: Các số đặc trưng của mẫu số liệu không ghép nhóm
  • Chương V: Vectơ
  • Chương 5: THỐNG KÊ
  • Chương VI: Một số yếu tố thống kê và xác suất
  • Chương VI: Thống kê
  • Hoạt động thực hành trải nghiệm
  • Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC
  • Chương VII: Phương pháp tọa độ trong mặt phẳng
  • Chương VI: Hàm số, đồ thị và ứng dụng
  • Hoạt động thực hành và trải nghiệm
  • Ôn tập cuối năm môn Đại số
  • Chương VII: Phương pháp tọa độ trong mặt phẳng
  • Chương VII: Bất phương trình bậc hai một ẩn
  • Thực hành phần mềm GeoGebra
  • Chương VIII: Đại số tổng hợp
  • Chương VIII: Đại số tổ hợp
  • Chương 1: VECTƠ
  • Chương IX: Tính xác suất theo định nghĩa cổ điển
  • Chương IX: Phương pháp tọa độ trong mặt phẳng
  • Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
  • Chương X: Xác suất
  • Bài tập ôn tập cuối năm
  • Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
  • Hoạt động thực hành và trải nghiệm
  • Ôn tập cuối năm môn Hình học
Hình học 10
  • Lý thuyết
  • Trắc nghiệm
  • Giải bài tập SGK
  • Hỏi đáp
  • Đóng góp lý thuyết
Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp ๖ۣۜNh◕k ๖ۣۜSilver ๖ۣۜBul...
  • ๖ۣۜNh◕k ๖ۣۜSilver ๖ۣۜBul...
9 tháng 1 2016 lúc 20:37

CM công thức HÊ RÔNG dùng để tính diện tích tam giác

Lớp 10 Toán Hình học 10 3 0 Khách Gửi Hủy Võ Thị Mỹ Duyên Võ Thị Mỹ Duyên 10 tháng 1 2016 lúc 7:53

Trong hình học, Công thức Heron cho rằng diện tích (S) của một tam giác có độ dài 3 cạnh lần lượt là a, b, và c là

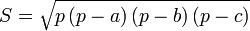
S={\sqrt {p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}

với p là nửa chu vi của tam giác:

p={\frac {a+b+c}{2}}.

Công thức Heron còn có thể được viết:

S={\ {\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}}\ \over 4}S={\ {\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\,}}\ \over 4}S={\ {\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})\,}}\ \over 4}. Đúng 0 Bình luận (0) Khách Gửi Hủy Võ Thị Mỹ Duyên Võ Thị Mỹ Duyên 10 tháng 1 2016 lúc 8:07

Trong hình học, Công thức Heron cho rằng diện tích (S) của một tam giác có độ dài 3 cạnh lần lượt là a, b, và c là

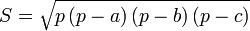
S={\sqrt {p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}

với p là nửa chu vi của tam giác:

p={\frac {a+b+c}{2}}.

Công thức Heron còn có thể được viết:

S={\ {\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}}\ \over 4}S={\ {\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\,}}\ \over 4}S={\ {\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})\,}}\ \over 4}.=> ĐPCM(Bổ sung thêm) Đúng 0 Bình luận (0) Khách Gửi Hủy ๖ۣۜNh◕k ๖ۣۜSilver ๖ۣۜBul... ๖ۣۜNh◕k ๖ۣۜSilver ๖ۣۜBul... 16 tháng 1 2016 lúc 17:31

anh_hung_lang_la  Cậu đi cảm ơn bác gồ đi!!!

 

Đúng 0 Bình luận (0) Khách Gửi Hủy Các câu hỏi tương tự Mai Hải Dương
  • Mai Hải Dương
14 tháng 2 2016 lúc 15:14

Hình thang ABCD có đáy AB= 6cm và CD =10cm.Nối AC ta dc tam giác ABC có diện tích 15 cm2.

a.tính dt của hình thnag ABCD.

blấy M và N là trung điểm của AD và BC .tính dt hình thang

Xem chi tiết Lớp 10 Toán Hình học 10 0 0 Lê Song Tuệ
  • Lê Song Tuệ
1 tháng 3 2016 lúc 19:21

a) cho ABC ,vẽ đường thẳng đi qua A cắt BC tại K và cắt trung tuyến BM tại I sao cho BI:IM= 1:2 Tính ti số diện tích của tam giác ABK và điện tích tam giác ABC   b) Cho tam giác ABC có 3 đường cao AD,BE,CF thỏa mãn AD+BC=BE+AC=CF+AB Chứng minh tam giác ABC là tam giác đều

Xem chi tiết Lớp 10 Toán Hình học 10 0 0 Phạm Vũ Anh Thư
  • Phạm Vũ Anh Thư
9 tháng 3 2016 lúc 15:53

hãy biểu diễn các điểm A(-2; 2), B(3; 3), C(2; -2) trên mặt phẳng tọa độ Oxy. Sau đó tính diện tích tam giác ABC.

Xem chi tiết Lớp 10 Toán Hình học 10 2 0 Thu Trang
  • Thu Trang
11 tháng 2 2016 lúc 14:26

 Cho (O, R) và dây cung AB cố định ( AB< 2R). Gọi C là điểm di động trên cung lớn AB. M; N là điểm chính giữa cung AC; cung AB. H là giao điểm MN và AC, K là giao điểm BM và CN. Chứng minh HKCM là tứ giác nội tiếp;Chứng minh tam giác CKM cân;Chứng minh K cách đều các cạnh tam giác ABC;Xác định vị trí điểm C để diện tích tứ giác AKBN đạt giá trị lớn nhất.

Xem chi tiết Lớp 10 Toán Hình học 10 0 0 Kiên NT
  • Kiên NT
21 tháng 2 2016 lúc 0:49 Bài 11:Cho đường tròn(O) đường kính AB2R. Điểm C thuộc đường tròn(C không trùng với A và B).Trên nửa mặt phẳng bờ AB có chứa điểm C kẻ tiếp tuyến à với (O).Gọi M là điểm chính giữa cung nhỏ AC. Tia BC cắt Ax tại Q,AM cắt BC tại N, AC cắt BM tại P.a) Gọi K là điểm chính giữa cung AB(cung không chứa C).HỎi có thể xảy ra trường hợp 3 điểm Q,M,K thẳng hàng không?b) Xác định vị trí của C trên nửa đường tròn tâm O để đường tròn ngoại tiếp tam giác MNQ tiếp xúc với (O).Bài 12: Cho tứ giác ABCD có đường...Đọc tiếp

Bài 11:Cho đường tròn(O) đường kính AB=2R. Điểm C thuộc đường tròn(C không trùng với A và B).Trên nửa mặt phẳng bờ AB có chứa điểm C kẻ tiếp tuyến à với (O).Gọi M là điểm chính giữa cung nhỏ AC. Tia BC cắt Ax tại Q,AM cắt BC tại N, AC cắt BM tại P.

a) Gọi K là điểm chính giữa cung AB(cung không chứa C).HỎi có thể xảy ra trường hợp 3 điểm Q,M,K thẳng hàng không?

b) Xác định vị trí của C trên nửa đường tròn tâm O để đường tròn ngoại tiếp tam giác MNQ tiếp xúc với (O).

Bài 12: Cho tứ giác ABCD có đường chéo BD không là phân giác của góc ABC và góc CDA.Một điểm P nằm trong tứ giác sao cho góc PBC=góc DBA; góc PDC = góc BDA.Chứng minh rằng tứ giác ABCD nội tiếp khi và chỉ khi AP=CP

Bài 13:Cho tam giác ABC có chu vi bằng 2p không đổi ngoại tiếp 1 đường tròn(O).Dựng tiếp tuyến MN với (O) sao cho MN song song với AC;M thuộc cạnh AB,N thuộc cạnh BC.Tính AC theo p để độ dài đoạn MN đạt giá trị lớn nhất.

Bài 14: Trong một tam giác cho trước hãy tìm bán kính lớn nhất của hai đường tròn bằng nhau tiếp xúc ngoài nhau đồng thời mỗi đường tròn tiếp xúc với hai cạnh của tam giác đó.

Bài 15: Trên cạnh AB của tam giác ABC lấy một điểm D sao cho đường tròn nột tiếp tam giác ACD và BCD bằng nhau

a) Tính đoạn CD theo các cạnh của tam giác

b)CMR: Điều kiện cần và đủ để góc C = 90 độ là điện tích tam giác ABC bằng diện tích hình vuông cạnh CD

Bài 16: Cho hình thang vuông ABCD có AB là cạnh đáy nhỏ,CD là cạnh đáy lớn,M là giao của AC và BD.Biết rằng hình thang ABCD ngoại tiếp đường tròn bán kính R.Tính diện tích tam giác ADM theo R

Bài 17:Cho tam giác ABC không cân,M là trung điểm cạnh BC,D là hình chiếu vuông góc của A trên BC; E và F tương ứng là các hình chiếu vuông góc của B và C trên đường kính đi qua A của đường tròn ngoại tiếp tam giác ABC.CMR: M là tâm đường tròn ngoại tiếp tam giác DEF

Bài 18: Cho đoạn thẳng AB, điểm C nằm giữa A và B, Tia Cx vuông góc với AB.Trên tia Cx lấy D và E sao cho CECB=CACD=3√CECB=CACD=3. Đường tròn ngoại tiếp tam giác ADC cắt đường tròn ngoại tiếp tam giác BEC tại H(H khác C). CMR: HC luôn đi qua một điểm cố định khi C chuyển động trên đoạn AB.Bài toán còn đúng không khi thay 3√3 bởi m cho trước(m>0)

Bài 19: Cho tam giác ABC nhọn và điểm M chuyện động trên đường thẳng BC.Vẽ trung trực của các đoạn BM và CM tương ứng cắt các đường thẳng AB và AC tại P và Q.CMR: Đường thẳng qua M và vuông góc với PQ đi qua 1 điểm cố định

Bài 20: Cho tam giác ABC và một đường tròn (O) đi qua A và C.Gọi K và N là các giao điểm của (O) với các cạnh AB,C.ĐƯờng tròn (O1) và (O2) ngoại tiếp tam giác ABC và tam giác KBN cắt nhau tại B và M.CMR: O1O2 song song với OM

 

Giúp t vs..^^^

Xem chi tiết Lớp 10 Toán Hình học 10 6 0 nguyễn hương giang
  • nguyễn hương giang
5 tháng 9 2015 lúc 17:24

Cho (O) đường kính AB=2R. Kẻ tiếp tuyến Ax với (O), lấy điểm E thuộc tia Ax sao cho AE>R. Kẻ tiếp tuyến EM tới (O) (M thuộc(O)) và M khác A a) CM OE vuông góc AM và BM // OEb) Đương thẳng vuông góc AB tại O cắt BM tại N. Xác định dạng của tứ giác OBNE?c) Cho R=3cm; OE=5cm. Tính diện tích tứ giác OBME?

Xem chi tiết Lớp 10 Toán Hình học 10 1 0 Nguyễn Ngô Anh Tuấn
  • Nguyễn Ngô Anh Tuấn
28 tháng 7 2015 lúc 9:44 LỚP 10 : HÌNH HỌC CHƯƠNG 2 :TÍCH VÔ HƯỚNG CỦA HAI VECTƠ .Bài 1 : Trong hệ tọa độ oxy . Cho 3 điểm A ( -1 ; 1 ) , B ( 1 ; 3 ) , C ( 1 ; -1 ) .a CM : 3 điểm ABC không thẳng hàng . b Tìm tọa độ trọng tâm tam giác ABC . c Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành . dCM : tam giác ABC vuông cân tại A . eTìm tọa độ điểm E sao cho tam giác ABE vuông cân tại A . g Tìm tọa độ điểm M nằm trên trục hoành sao cho tam giác OMA cân tại O .Đọc tiếp

LỚP 10 : HÌNH HỌC 

CHƯƠNG 2 :TÍCH VÔ HƯỚNG CỦA HAI VECTƠ .

Bài 1 : Trong hệ tọa độ oxy . Cho 3 điểm A ( -1 ; 1 ) , B ( 1 ; 3 ) , C ( 1 ; -1 ) .

a> CM : 3 điểm ABC không thẳng hàng . 

b> Tìm tọa độ trọng tâm tam giác ABC . 

c> Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành . 

d>CM : tam giác ABC vuông cân tại A . 

e>Tìm tọa độ điểm E sao cho tam giác ABE vuông cân tại A . 

g> Tìm tọa độ điểm M nằm trên trục hoành sao cho tam giác OMA cân tại O .

Xem chi tiết Lớp 10 Toán Hình học 10 1 1 Đoàn Minh Trang
  • Đoàn Minh Trang
25 tháng 3 2016 lúc 10:50

Tính thể tích và diện tích toàn phần của một hình chóp cụt đều có đáy lớn là hình vuông cạnh 6cm. Đáy nhỏ là hình vuông cạnh 3cm. Đường cap bằng 4cm

Xem chi tiết Lớp 10 Toán Hình học 10 1 0 Liên Mỹ
  • Liên Mỹ
31 tháng 12 2015 lúc 14:08

cho tam giác ABC có 3 cạnh góc nhọn trung tuyến AM có độ dài bằng cạnh BC. Đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự D và E. đường tròn ngoại tiếp tam giác ADE và đường tròn ngoại tiếp tam giác ABC cắt AM lần lượt tịa I và J.chứng minh BDIM  nội tiếp, BIJC là hình bình hành

Xem chi tiết Lớp 10 Toán Hình học 10 2 0

Khoá học trên OLM (olm.vn)

  • Toán lớp 10 (Kết nối tri thức với cuộc sống)
  • Toán lớp 10 (Cánh Diều)
  • Toán lớp 10 (Chân trời sáng tạo)
  • Ngữ văn lớp 10 (Kết nối tri thức với cuộc sống)
  • Ngữ văn lớp 10 (Cánh Diều)
  • Ngữ văn lớp 10 (Chân trời sáng tạo)
  • Tiếng Anh lớp 10 (i-Learn Smart World)
  • Tiếng Anh lớp 10 (Global Success)
  • Vật lý lớp 10 (Kết nối tri thức với cuộc sống)
  • Vật lý lớp 10 (Cánh diều)
  • Hoá học lớp 10 (Kết nối tri thức với cuộc sống)
  • Hoá học lớp 10 (Cánh diều)
  • Sinh học lớp 10 (Kết nối tri thức với cuộc sống)
  • Sinh học lớp 10 (Cánh diều)
  • Lịch sử lớp 10 (Kết nối tri thức với cuộc sống)
  • Lịch sử lớp 10 (Cánh diều)
  • Địa lý lớp 10 (Kết nối tri thức với cuộc sống)
  • Địa lý lớp 10 (Cánh diều)
  • Giáo dục kinh tế và pháp luật lớp 10 (Kết nối tri thức với cuộc sống)
  • Giáo dục kinh tế và pháp luật lớp 10 (Cánh diều)
  • Lập trình Python cơ bản

Khoá học trên OLM (olm.vn)

  • Toán lớp 10 (Kết nối tri thức với cuộc sống)
  • Toán lớp 10 (Cánh Diều)
  • Toán lớp 10 (Chân trời sáng tạo)
  • Ngữ văn lớp 10 (Kết nối tri thức với cuộc sống)
  • Ngữ văn lớp 10 (Cánh Diều)
  • Ngữ văn lớp 10 (Chân trời sáng tạo)
  • Tiếng Anh lớp 10 (i-Learn Smart World)
  • Tiếng Anh lớp 10 (Global Success)
  • Vật lý lớp 10 (Kết nối tri thức với cuộc sống)
  • Vật lý lớp 10 (Cánh diều)
  • Hoá học lớp 10 (Kết nối tri thức với cuộc sống)
  • Hoá học lớp 10 (Cánh diều)
  • Sinh học lớp 10 (Kết nối tri thức với cuộc sống)
  • Sinh học lớp 10 (Cánh diều)
  • Lịch sử lớp 10 (Kết nối tri thức với cuộc sống)
  • Lịch sử lớp 10 (Cánh diều)
  • Địa lý lớp 10 (Kết nối tri thức với cuộc sống)
  • Địa lý lớp 10 (Cánh diều)
  • Giáo dục kinh tế và pháp luật lớp 10 (Kết nối tri thức với cuộc sống)
  • Giáo dục kinh tế và pháp luật lớp 10 (Cánh diều)
  • Lập trình Python cơ bản

Từ khóa » Hê Rông Cho Tứ Giác