Công Thức Hàm Số Lượng Giác - Xét Tính Chẵn Lẻ, Tính Tuần Hoàn Và ...
Có thể bạn quan tâm
Hàm số lượng giác sin và hàm số lượng giác côsin
- Công thức đạo hàm
- Công thức nguyên hàm
1 . Hàm số lượng giác sin
Hàm số y=sinx có tập xác định R là −1≤sinx≤1,∀x∈R.
y=sinx là hàm số lẻ.
y=sinx là hàm số tuần hoàn với chu kì 2π.
Hàm số y=sinx nhận các giá trị đặc biệt:
* sinx=0 khi x=kπ,k∈Z.
* sinx=1 khi x=π2+k2π,k∈Z.
* sinx=−1 khi x=−π2+k2π,k∈Z.
Công thức hàm số y= sinx
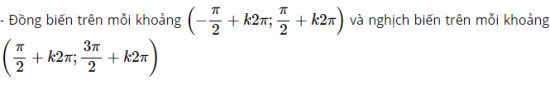
Đồ thị hàm số y=sinx:
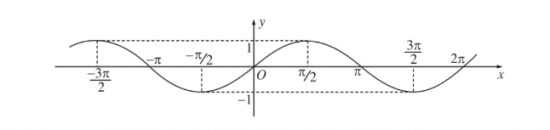
- Là hàm số lẻ
- Là hàm số tuần hoàn với chu kì 2π
Bảng biến thiên của hàm số y = sinx trên đoạn [ -π; π ]
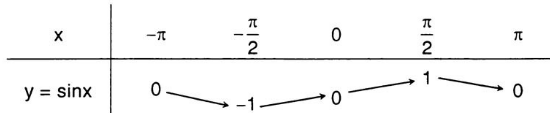
2. Hàm số lượng giác côsin
Hàm số y=cosx có tập xác định R là −1≤cosx≤1,∀x∈R.
y=cosx là hàm số chẵn.
y=cosx là hàm số tuần hoàn với chu kì 2π.
Hàm số y=cosx nhận các giá trị đặc biệt:
+ cosx=0 khi x=π2+kπ,k∈Z .
+ cosx=1 khi x=k2π,k∈Z.
+ cosx=−1 khi x=(2k+1)π,k∈Z.
Công thức hàm số y = Cosx
![]()
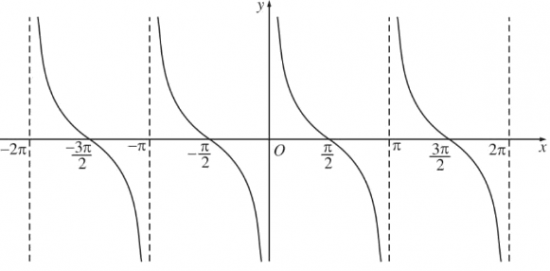
Đồ thị hàm số y=cosx:
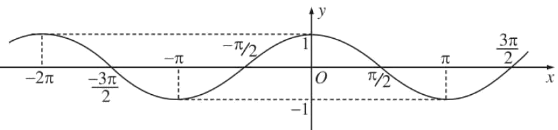
- Là hàm số chẵn
- Là hàm số tuần hoàn với chu kì 2π
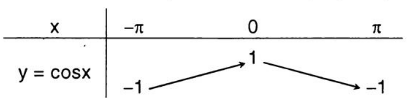
Bảng biến thiên của hàm số y = cosx trên đoạn [ -π ; π ]
Hàm số lượng giác tang và côtang
1. Hàm số lượng giác tang
Hàm số y=tanx=sinxcosx có tập xác định R là D=R∖{π2+kπ,k∈Z}.
y=tanx là hàm số lẻ.
y=tanx là hàm số tuần hoàn với chu kì π.
Hàm số y=tanx nhận các giá trị đặc biệt:
+ tanx=0 khi x=kπ,k∈Z.
+ tanx=1 khi x=π4+kπ,k∈Z.
+ tanx=−1 khi x=−π4+kπ,k∈Z .
Công thức hàm số y = tanx
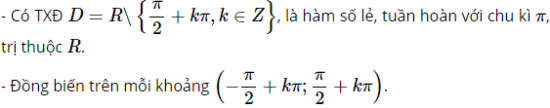
Đồ thị hàm số y=tanx:
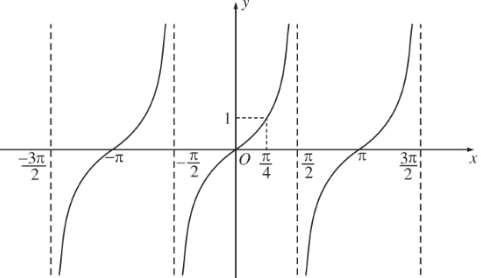
- Là hàm số lẻ
- Là hàm số tuần hoàn với chu kì π
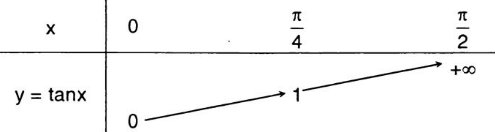
Bảng biến thiên của hàm số y = tanx trên [ 0; π/2)
2. Hàm số lượng giác côtang
Hàm số y=cotx=cosxsinx có tập xác định R là D=R∖{kπ,k∈Z}.
y=cotx là hàm số lẻ.
y=cotx là hàm số tuần hoàn với chu kì π.
Hàm số y=cotx nhận các giá trị đặc biệt:
+ cotx=0 khi x=π2+kπ,k∈Z.
+ cotx=1 khi x=π4+kπ,k∈Z.
+ cotx=−1 khi x=−π4+kπ,k∈Z.
Công thức hàm số y = cotx
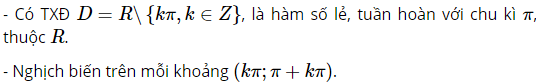
Đồ thị hàm số y=cotx:
- Là hàm số lẻ
- Là hàm số tuần hoàn với chu kì π
Sự biến thiên và đồ thị của hàm số y = cotx trên khoảng ( 0 đến π)
Từ khóa » Hàm Số Cosx
-
Lý Thuyết Hàm Số Lượng Giác | SGK Toán Lớp 11
-
Bài 1. Hàm Số Lượng Giác - Củng Cố Kiến Thức
-
Bài 1: Hàm Số Lượng Giác - Hoc24
-
Phương Pháp Giải Bài Tập Toán 11 – Phần Hàm Số Lượng Giác
-
Giải Toán 11 Bài 1. Hàm Số Lượng Giác
-
Hàm Số Lượng Giác Cơ Bản (sinx Và Cosx).
-
Hàm Số (y = Cos X ) Nghịch Biến Trên Mỗi Khoảng:
-
Lý Thuyết Hàm Số Lượng Giác - Môn Toán - Tìm đáp án, Giải Bài Tập, để
-
Lý Thuyết Và Các Công Thức Lượng Giác Đầy Đủ Nhất - Marathon
-
Dựa Vào đồ Thị Hàm Số Y = Cos X, Tìm Các Khoảng Giá Trị ... - Haylamdo
-
Đồ Thị Hàm Số Y=cosx Có Bao Nhiêu Trục đối Xứng? - MathVn.Com
-
Xét Tính Chẵn Lẻ Của Hàm Số Lượng Giác Như Thế Nào?
-
Chứng Minh Y=cosx Là Hàm Số Chẵn Chính Xác Nhất - Top Lời Giải