Công Thức Tính Gia Tốc

3.7/5 - (3 bình chọn)

Tất các công thức tính gia tốc và Bài tập liên quan. Các bạn theo dõi thông tin bài viết sau đây để có thêm thông tin hữu ích

Mục Lục

Toggle

• Gia tốc là gì?
• Các công thức liên quan đến tính gia tốc
• Bài tập liên quan đến tính gia tốc
• Công thức tính gia tốc tổng quát
• Công thức tính gia tốc tức thời
• Công thức tính Gia tốc trung bình
• Công thức tính gia tốc tiếp tuyến
• Công thức tính gia tốc trọng trường
• Công thức tính gia tốc toàn phần
• Công thức liên hệ giữa gia tốc, vận tốc và quãng đường
• Công thức tính gia tốc và gia tốc rơi tự do
• Gia tốc pháp tuyến
• Gia tốc tiếp tuyến
• Công thức tính gia tốc hướng tâm?

Gia tốc là gì?

Gia tốc là đại lượng đặc trưng cho sự thay đổi của vận tốc theo thời gian. Hiểu cách khác gia tốc là mức độ thay đổi của vận tốc trong quá trình di chuyển của một vật. Khi duy trì vận tốc không đổi nghĩa là vật đó không tăng tốc. Gia tốc chỉ xuất hiện khi có sự thay đổi của vận tốc. Vận tốc sẽ thay đổi theo ở một mức độ cố định, đối tượng đang di chuyển với một gia tốc là hằng số. Trong hệ đơn vị quốc tế SI, gia tốc có đơn vị là m/s2 nghĩa là m/s mỗi giây.

Hay nói một cách dễ hiểu hơn thì gia tốc là đại lượng vật lý đặc trưng cho sự chuyển đổi nhanh hay chậm của vận tốc cả về hướng và độ lớn, Vận tốc và gia tốc là đại lượng của véc tơ. Nhìn vào số đo của gia tốc là bạn có thể biết được vật đó thay đổi vận tốc nhanh hay chậm. Gia tốc là một trong những đại lượng quan trọng trong vật lý, vì nó giúp mô tả chuyển động của các vật trong không gian và thời gian.

Chuyển động tăng tốc khi vecto gia tốc cùng chiều với chuyển động, giảm tốc khi vecto gia tốc ngược chiều với chiều chuyển động, đổi hướng khi vecto gia tốc có phương khác với phương chuyển độn

Ví dụ: Nếu bạn đang lái xe và bất ngờ đạp chân ga thật mạnh, xe của bạn sẽ có gia tốc dương (dương vì tốc độ đang tăng lên). Ngược lại, nếu bạn đạp chân phanh thật mạnh, xe của bạn sẽ có gia tốc âm (âm vì tốc độ đang giảm xuống).

Một số loại gia tốc mà chúng ta thường sẽ găp như sau:

– Gia tốc tức thời

– Gia tốc trung bình

– Gia tốc pháp tuyến

– Gia tốc tiếp tuyến

– Gia tốc toàn phần

– Gia tốc trọng trường

Các công thức liên quan đến tính gia tốc

– Công thức tính gia tốc tổng quát:

– Công thức tính gia tốc tức thời:

Gia tốc tức thời của vật là biểu diễn cho sự thay đổi vận tốc của vật đó trong môt khoảng cách thời gian vô cùng nhỏ ( tức thời)

Trong đó thì:

v là vận tốc đơn vị m/s

t là thời gian đơn vị s

– Công thức tính gia tốc trung bình: Gia tốc trung bình của vật biểu diễn cho sự thay đổi vận tốc của vật đó trong một khoảng thời gian nhất định. Gia tốc trung bình là biến thiên của vận tốc được chai cho biến thiên thời gian.

Trong đó thì:

v là tốc độ tức thời m/s

r là độ bán kính cong m

Lưu ý: Trong trường hợp vật chuyển động tròn đều, thì v và R đều là các đại lượng không đổi. Do đó gia tốc pháp tuyến trong trường hợp này là gia tốc hướng tâm và không đổi.

– Công thức tính gia tốc tiếp tuyến: Gia tốc tiếp tuyến là đại lương mô tả cho sự thay đổi độ lớn vecto vận tốc. Gia tốc tiếp tuyến thì có các điểm như là phương trùng với phương của tiếp tuyến, cùng chiều khi chuyển động nhanh dần và ngược chiều khi chuyển động chậm dần

Quan hệ giữa gia tốc tiếp tuyến và gia tốc pháp tuyến. Gia tốc trong chuyển động hình cong bao gồm có hai phần.

+ Gia tốc pháp tuyến: đây là đặc trưng cho sự thay đổi về phương của vận tốc theo thời gian

+ Gia tốc tuyến tuyến đặc trưng cho sự thay đổi về hướng và vận tốc theo thời gian

– Công thức tính gia tốc toàn phần: Gia tốc toàn phần là tổng của hai gia tốc là gia tốc tiếp tuyến và gia tốc pháp tuyến theo vecto.

– Công thức liên hệ giữa gia tốc, vận tốc và quãng đường.

Theo đó thì ta sẽ chứng minh mối liên hệ của gia tốc, vận tốc và quãng đường như sau:

Để áp dụng công thức tính gia tốc để giải quyết các bài tập vật lý liên quan đến gia tốc, bạn có thể làm theo các bước sau đây:

Bước 1: Xác định các thông số về vận tốc và thời gian. Để tính gia tốc, bạn cần biết các thông số về vận tốc và thời gian. Vận tốc có thể được cho trong đề bài hoặc được tính toán từ các thông số khác như quãng đường di chuyển và thời gian di chuyển. Thời gian cũng có thể được cho trong đề bài hoặc là kết quả của phép tính thời gian.

Bước 2: Áp dụng công thức tính gia tốc.

Sử dụng công thức gia tốc: a = (v – v0)/(t – t0) = Δv/Δt, trong đó a là gia tốc, v là vận tốc hiện tại, v0 là vận tốc ban đầu, t là thời gian hiện tại, t0 là thời gian ban đầu, Δv là sự thay đổi vận tốc và Δt là sự thay đổi thời gian. Dựa trên các thông số đã xác định ở bước 1, bạn có thể tính toán gia tốc của vật.

Bước 3: Giải quyết bài tập vật lý liên quan đến gia tốc.

Dựa trên kết quả tính toán gia tốc thu được, bạn có thể sử dụng nó để giải quyết các bài tập vật lý liên quan đến gia tốc, chẳng hạn như tính lực tác động lên vật, khoảng cách di chuyển của vật hoặc tốc độ của vật sau một khoảng thời gian nhất định. Với những bài tập phức tạp hơn, bạn có thể cần sử dụng nhiều công thức và phương pháp tính toán khác nhau để giải quyết. Việc rèn luyện và nắm chắc kiến thức vật lý cơ bản sẽ giúp bạn giải quyết các bài tập liên quan đến gia tốc một cách dễ dàng và chính xác.

Bài tập liên quan đến tính gia tốc

1: Một chiếc xe tăng tốc đều từ 18,5 m/s lên 46,1 m/s trong vòng 2,37 giây. Gia tốc trung bình của nó là bao nhiêu?

Viết phương trình: a = Δv / Δt = (vf – vi)/(tf – ti)

Xác định các biến: vf = 46,1 m/s, vi = 18,5 m/s, tf = 2,47 s, ti = 0 s.

Giải: a = (46,1 – 18,5)/2,47 = 11,17 m/s2.

2: Vật chuyển động theo chiều Dương của trục Ox với vận tốc v không đổi.

A. Thì tọa độ của vật luôn có giá trị (+).

B. vận tốc của vật luôn có giá tri (+).

C tọa độ và vận tốc của vật luôn có giá trị (+).

D. tọa độ luôn trùng với quãng đường.

Đáp án chính xác: B. vận tốc của vật luôn có giá tri (+).

3: Xe chạy quảng đường 48km hết t giây. Trong 1/4 khoảng thời gian đầu nó chạy với tốc độ trung bình là v1 = 30 km/h. Tìm vận tốc trung bình trong khoảng thời gian còn lại:

A. 56 km/h.

B. 50 km/h.

C. 52 km/h.

D. 54 km/h.

Đáp án chính xác: D. 54 km/h.

Lời giải:

Quãng đường xe chạy từ A đến B sẽ là: s = 48t.

Quãng đường xe chạy trong t/4: s1 = 30.t/4

Tốc độ trung bình trong khoảng thời gian còn lại là:

Vtb= (48t- 7,5t)/0,75t= 54km/h

4.Một đối tượng được ném lên với vận tốc ban đầu 20 m/s và đạt đến độ cao 10 m. Tính thời gian mà đối tượng đạt đến độ cao này và gia tốc của đối tượng tại thời điểm đó.

Giải:

Đối tượng đạt đến độ cao 10 m tương ứng với thời gian di chuyển lên tại đó được tính bằng công thức: S = 1/2 x a x t^2

Trong đó,

S là quãng đường di chuyển, a là gia tốc, và t là thời gian.

10 = 1/2 x 9,8 x t^2

t = √(10/4.9) = 1,43 s

Thời gian di chuyển lên tại độ cao 10 m là 1,43 s.

Gia tốc của đối tượng tại thời điểm này được tính bằng công thức:

a = v^2/2h

Trong đó, v là vận tốc ban đầu của đối tượng, và h là độ cao đối tượng đạt được.

a = 20^2/(2*10) = 20 m/s^2

Vậy gia tốc của đối tượng tại thời điểm đạt đến độ cao 10 m là 20 m/s^2.

Công thức tính gia tốc tổng quát

Công thức tính gia tốc tổng quát

Công thức tính gia tốc tức thời

Gia tốc tức thời của vật là biểu diễn cho sự thay đổi vận tốc của vật đó trong một khoảng thời gian vô cùng nhỏ (tức thời).

Công thức:

Trong đó với:

• v là vận tốc đơn vị m/s
• t là thời gian đon vị s

Công thức tính Gia tốc trung bình

Gia tốc trung bình của vật biểu diễn cho sự thay đôi vận tốc của vật đó trong một khoảng thời gian nhất định.

Gia tốc trung bình là biễn thiên của vận tốc được chia cho biễn thiên thời gian

Công thức:

Trong đó:

• v là tốc độ tức thời (m/s)
• R là độ dài bán kính cong (m)

Lưu ý: Trong trường hợp vật chuyển động tròn đều, thì v và R đều là các đại lượng không đổi. Do đó gia tốc pháp tuyến trong trường hợp này là gia tốc hướng tâm và không đổi.

Tính gia tốc trung bình từ hai vận tốc

Xác định phương trình gia tốc trung bình

Bạn có thể tính gia tốc trung bình của một vật trong một khoảng thời gian nào đó dựa vào vận tốc của nó (tốc độ di chuyển theo một hướng cụ thể) trước và sau quãng thời gian đó. Để làm vậy, bạn cần biết phương trình gia tốc: a = Δv / Δt, trong đó, a là gia tốc, Δv là độ thay đổi của vận tốc và Δt là thời gian cần để có được sự thay đổi đó.

Đơn vị tính của gia tốc là mét trên giây trên giây hay m/s2.

Gia tốc là một đại lượng véc-tơ, nghĩa là nó có cả độ lớn lẫn hướng. Độ lớn của gia tốc là tổng lượng gia tốc, còn hướng là đường di chuyển của đối tượng. Khi đối tượng di chuyển chậm dần, ta có gia tốc âm.

Hiểu các biến số

Bạn có thể định nghĩa kỹ hơn Δv và Δt: Δv = vf – vi và Δt = tf – ti, trong đó vf là vận tốc cuối cùng, vi là vận tốc ban đầu, tf là thời gian kết thúc và ti là thời gian bắt đầu.

Bởi gia tốc là một đại lượng có hướng, việc luôn lấy vận tốc cuối để trừ cho vận tốc ban đầu là vô cùng quan trọng. Nếu làm ngược lại, hướng của gia tốc sẽ không chính xác.

Trừ khi bài toán cho khác đi, thời gian bắt đầu thường là 0 giây.

Dùng công thức tính gia tốc

Đầu tiên, hãy viết ra phương trình và mọi biến đã biết của bạn. Phương trình là a = Δv / Δt = (vf – vi)/(tf – ti). Lấy hiệu giữa vận tốc cuối và vận tốc ban đầu rồi chia kết quả thu được cho quãng thời gian. Kết quả cuối cùng chính là gia tốc trung bình trong thời gian đó.

Nếu vận tốc cuối nhỏ hơn vận tốc ban đầu, gia tốc sẽ là đại lượng mang giá trị âm hay đó chính là tốc độ di chuyển chậm lại của đối tượng.

Ví dụ 1: Một chiếc xe tăng tốc đều từ 18,5 m/s lên 46,1 m/s trong vòng 2,37 giây. Gia tốc trung bình của nó là bao nhiêu?

Viết phương trình: a = Δv / Δt = (vf – vi)/(tf – ti)

Xác định các biến: vf = 46,1 m/s, vi = 18,5 m/s, tf = 2,47 s, ti = 0 s.

Giải: a = (46,1 – 18,5)/2,47 = 11,17 m/s2.

Ví dụ 2: Một người đi mô-tô đang di chuyển với tốc độ 22,4 m/s thì đạp thắng và dừng lại sau 2,55 s. Tìm gia tốc của người đó.

Viết phương trình: a = Δv / Δt = (vf – vi)/(tf – ti)

Xác định các biến: vf = 0 m/s, vi = 22,4 m/s, tf = 2,55 s, ti = 0 s.

Giải: a = (0 – 22,4)/2,55 = -8,78 m/s2.

Công thức tính gia tốc tiếp tuyến

Gia tốc tiếp tuyến là đại lượng mô tả cho sự thay đổi độ lớn vecto vận tốc. Gia tốc tiếp tuyến có các điểm lưu ý sau:

• Phương trùng với phương của tiếp tuyến
• Cùng chiều khi chuyển động nhanh dần và ngược chiều khi chuyển động chậm dần.

Công thức gia tốc tiếp tuyến:

Quan hệ giữa gia tốc tiếp tuyến và gia tốc pháp tuyến: Gia tốc trong chuyển động hình cong bao gồm hai phần:

• Gia tốc pháp tuyến – Đặc trưng cho sự thay đổi về phương của vận tốc theo thời gian
• Gia tốc tuyến tuyến – Đặc trưng cho sự thay đổi về hướng của vận tốc theo thời gian

Công thức tính gia tốc trọng trường

– Gia tốc trọng trường (g) là gia tốc do lực hấp dẫn tác dụng lên một vật.

– Tại một nơi nhất định trên Trái Đất và ở gần mặt đất, mọi vật đều rơi tự do với cùng gia tốc g. Gia tốc rơi tự do ở các vĩ độ khác nhau trên Trái Đất thì khác nhau. Người ta thường lấy g ≈ 9,8 m/s2 hoặc g ≈ 10 m/s2 .

– Theo Niu – tơn thì trọng lực mà Trái Đất tác dụng lên một vạt là lực hấp dẫn giữa Trái Đất và vật đó. Trọng lực đặt vào một điểm đặc biệt của vật, gọi là trọng tâm của vật. Độ lớn của trọng lực (tức trọng lượng) bằng:

Công thức

Trong đó:

+ h là độ cao của vật so với mặt đất (m)

+ M và R lần lượt là khối lượng và bán kính của Trái Đất

+ m là khối lượng của vật

Kiến thức mở rộng

Cũng như vận tốc, gia tốc trọng trường là đại lượng có hướng.

– Lập tỉ số ta tính được gia tốc tại độ cao h so với mặt đất:

Trong đó:

+ gh là gia tốc tại độ cao h so với mặt đất

+ g0 là gia tốc tại mặt đất

+ R là bán kính của Trái đất

+ h là độ cao của vật so với mặt đất

Gia tốc trọng trường là gì?

Gia tốc trọng trường là đại lượng của gia tốc do lực hấp dẫn tác dụng lên vật. Khi bỏ qua ma sát do lực cản không khí, theo nguyên lý tương đương thì mọi vật đều chịu một gia tốc trong trường hấp dẫn là giống nhau đối với tâm khối lượng của vật.

Gia tốc trọng trường giống nhau đối với mọi vật chất và khối lượng. Gia tốc trọng trường thường do lực hút của tái đất gây nên thường khác nhau tại các điểm và dao động từu: 9.78 – 9.83. Tuy nhiên, trong các bài tập thì người ta thường lấy bằng 10 m/s2

Bài tập minh họa

Câu 1:Tìm gia tốc rơi tự do tại một nơi có độ cao bằng nửa bán kính trái đất. Biết gia tốc trọng trường tại mặt đất là g=10 m/s2.

Lời giải:

Gia tốc ở mặt đất:

Gia tốc ở độ cao h:

Câu 2: Gia tốc rơi tự do trên bề mặt của mặt trăng là 1,6m/s2 và RMT = 1740km. Hỏi ở độ cao nào so với mặt trăng thì g = 1/9 gMT.

Lời giải:

Công thức tính gia tốc toàn phần

Gia tốc toàn phần hiểu đơn giản là tổng của hai gia tốc là gia tốc tiếp tuyến và gia tốc pháp tuyến theo vecto. Công thức tính như sau:

Công thức liên hệ giữa gia tốc, vận tốc và quãng đường

Ta sẽ chứng minh mối liên hệ của gia tốc, vận tốc và quãng đường

Chứng minh:

Một số bài tập về gia tốc

A. Trắc nghiệm

Câu 1: Đoạn đường dài 40km với vận tốc trung bình 80km/h. Trên đoạn đường 40 km tiếp theo với tốc độ trung bình là 40 km/h. Tìm tốc độ trung bình xe trong cả quãng đường 80km bao nhiêu?

A. 53 km/h.

B. 65 km/h.

C. 60 km/h.

D. 50 km/h.

Gợi ý đáp án

A. 53 km/h.

Bởi vì

Thời gian chuyển động trên đoạn đường 80 km của xe là: t = 0,5 + 1 = 1,5 h

Suy ra: Tốc độ trung bình vtb = 80/15 ≈ 53 km/h.

Câu 2: Xe chạy quảng đường 48km hết t giây. Trong 1/4 khoảng thời gian đầu nó chạy với tốc độ trung bình là v1 = 30 km/h. Tìm vận tốc trung bình trong khoảng thời gian còn lại:

A. 56 km/h.

B. 50 km/h.

C. 52 km/h.

Gợi ý đáp án

D. 54 km/h.

giải chi tiết như sau:

• Quãng đường xe chạy từ A đến B sẽ là: s = 48t.
• Quãng đường xe chạy trong t/4: s1 = 30.t/4

Tốc độ trung bình trong khoảng thời gian còn lại là:

Câu 3: Một chiếc xe chuyển động vối vận tốc v. Khẳng định nào sau đây là đúng?

A. Xe chắc chắn chuyển động thẳng đều với tốc độ là v.

B. Quãng đường xe chạy được tỉ lệ thuận với thời gian chuyển động.

C. Tốc độ trung bình trên các quãng đường khác nhau trên đường thẳng AB có thể là khác nhau.

D. Thời gian chạy tỉ lệ với tốc độ v.

Gợi ý đáp án

C. Tốc độ trung bình trên các quãng đường khác nhau trên đường thẳng AB có thể là khác nhau.

Câu 4, Vật chuyển động theo chiều Dương của trục Ox với vận tốc v không đổi. Thì

A. tọa độ của vật luôn có giá trị (+).

B. vận tốc của vật luôn có giá tri (+).

C. tọa độ và vận tốc của vật luôn có giá trị (+).

D. tọa độ luôn trùng với quãng đường.

Gợi ý đáp án

B. vận tốc của vật luôn có giá tri (+).

Câu 5: Xe chuyển động trên quãng đường từ A đến B dài 10km sau đó lập tức quay ngược lại. Thời gian của hành trình này là 20 phút. Tính tốc độ trung bình của xe trong khoảng thời gian trên:

A. 20 km/h.

B. 30 km/h.

C. 60 km/h.

D. 40 km/h.

Gợi ý đáp án

C. 60 km/h.

Công thức tính gia tốc và gia tốc rơi tự do

Công thức tính gia tốc tổng quát

Gia tốc là mức độ thay đổi vận tốc trong quá trình chuyển động của một vật. Khi duy trì vận tốc không đổi, nghĩa là vật không tăng tốc. Gia tốc chỉ xuất hiện khi có sự thay đổi vận tốc. Khi vận tốc thay đổi theo một mức độ cố định, đối tượng đang di chuyển với một gia tốc là hằng số . Bạn có thể tính gia tốc theo đơn vị mét/giây/giây, dựa vào thời gian cần dùng để chuyển từ vận tốc này sang vận tốc khác hoặc dựa vào khối lượng của đối tượng.

Công thức tính gia tốc rơi tự do

Trước khi bắt tìm hiểu về công thức tính gia tốc rơi tự do bạn cần lưu ý những kiến thức liên quan đến sự rơi tự do.

Sự rơi của các vật trong không khí:

– Trong không khí không phải bao giờ vật nặng cũng rơi nhanh hơn vật nhẹ.

– Lực cản của không khí là nguyên nhân làm cho vật rơi nhanh, chậm khác nhau.

Sự rơi của các vật trong chân không (Sự rơi tự do):

– Nếu loại bỏ được ảnh hưởng của không khí thì mọi vật sẽ rơi nhanh như nhau. Sự rơi của các vật trong trường hợp này gọi là sự rơi tự do.

– Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực.

Gia tốc rơi tự do

– Tại một nơi nhất định trên Trái Đất và ở gần mặt đất, các vật đều rơi tự do với cùng một gia tốc 

– Gia tốc rơi tự do ở các nơi khác nhau trên Trái đất là khác nhau.

– Nếu không đòi hỏi độ chính xác cao, ta có thể lấy g = 9,8 m/s2 hoặc g ≈ 10 m/s2

Những đặc điểm của chuyển động rơi tự do

– Chuyển động rơi tự do:

+ có phương thẳng đứng.

+ có chiều từ trên xuống dưới.

+ là chuyển động thẳng nhanh dần đều.

– Khi thả vật rơi tự do không vận tốc đầu, có:

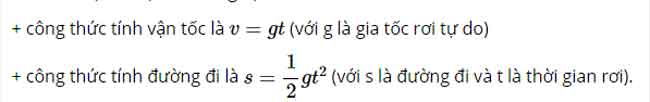
Gia tốc pháp tuyến

Gia tốc pháp tuyến đặc trưng cho sự thay đổi về phương của vận tốc. Đặc điểm gia tốc pháp tuyến sẽ là:

Phương vuông góc với tiếp tuyến của quỹ đạo vật

Chiều luôn hướng về phía lõm của quỹ đạo

Công thức của gia tốc pháp tuyến:

Trong đó:

v là tốc độ tức thời (m/s)

R là độ dài bán kính cong (m)

Lưu ý: Trong trường hợp vật chuyển động tròn đều, thì v và R đều là các đại lượng không đổi. Do đó gia tốc pháp tuyến trong trường hợp này là gia tốc hướng tâm và không đổi.

Gia tốc tiếp tuyến

Gia tốc tiếp tuyến là đại lượng mô tả cho sự thay đổi độ lớn vecto vận tốc. Gia tốc tiếp tuyến có các điểm lưu ý sau:

Phương trùng với phương của tiếp tuyến

Cùng chiều khi chuyển động nhanh dần và ngược chiều khi chuyển động chậm dần.

Công thức gia tốc tiếp tuyến:

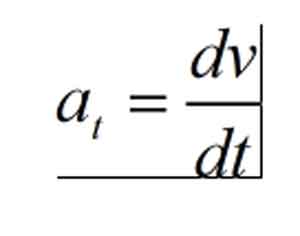
Quan hệ giữa gia tốc tiếp tuyến và gia tốc pháp tuyến: Gia tốc trong chuyển động hình cong bao gồm hai phần:

Gia tốc pháp tuyến – Đặc trưng cho sự thay đổi về phương của vận tốc theo thời gian

Gia tốc tuyến tuyến – Đặc trưng cho sự thay đổi về hướng của vận tốc theo thời gian

Bài tập về gia tốc

Câu 1: Một chiếc xe chuyển động vối vận tốc v. Khẳng định nào sau đây là đúng?

1. Xe chắc chắn chuyển động thẳng đều với tốc độ là v.

1. Quãng đường xe chạy được tỉ lệ thuận với thời gian chuyển động.

1. Tốc độ trung bình trên các quãng đường khác nhau trên đường thẳng AB có thể là khác nhau.

1. Thời gian chạy tỉ lệ với tốc độ v.

Đáp án chính xác:

C. Tốc độ trung bình trên các quãng đường khác nhau trên đường thẳng AB có thể là khác nhau.

Câu 2: Vật chuyển động theo chiều Dương của trục Ox với vận tốc v không đổi. Thì

1. tọa độ của vật luôn có giá trị (+).

1. vận tốc của vật luôn có giá tri (+).

1. tọa độ và vận tốc của vật luôn có giá trị (+).

1. tọa độ luôn trùng với quãng đường.

Đáp án chính xác:

B. vận tốc của vật luôn có giá tri (+).

Câu 3: Xe chuyển động trên quãng đường từ A đến B dài 10km sau đó lập tức quay ngược lại. Thời gian của hành trình này là 20 phút. Tính tốc độ trung bình của xe trong khoảng thời gian trên:

1. 20 km/h.

1. 30 km/h.

1. 60 km/h.

1. 40 km/h.

Đáp án chính xác:

C. 60 km/h.

Câu 4: Đoạn đường dài 40km với vận tốc trung bình 80km/h. Trên đoạn đường 40 km tiếp theo với tốc độ trung bình là 40 km/h. Tìm tốc độ trung bình xe trong cả quãng đường 80km bao nhiêu?

1. 53 km/h.

1. 65 km/h.

1. 60 km/h.

1. 50 km/h.

Đáp án chính xác: A. 53 km/h.

Lời giải:

Thời gian chuyển động trên đoạn đường 80 km của xe là: t = 0,5 + 1 = 1,5 h

Suy ra: Tốc độ trung bình vtb = 80/15 ≈ 53 km/h.

Câu 5: Xe chạy quảng đường 48km hết t giây. Trong 1/4 khoảng thời gian đầu nó chạy với tốc độ trung bình là v1 = 30 km/h. Tìm vận tốc trung bình trong khoảng thời gian còn lại:

1. 56 km/h.

1. 50 km/h.

1. 52 km/h.

1. 54 km/h.

Đáp án chính xác: D. 54 km/h.

Lời giải:

Quãng đường xe chạy từ A đến B sẽ là: s = 48t.

Quãng đường xe chạy trong t/4: s1 = 30.t/4

Tốc độ trung bình trong khoảng thời gian còn lại là:

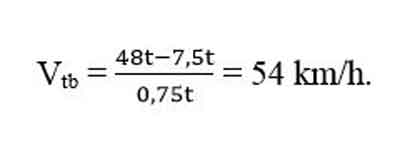
Bài tập tính gia tốc có lời giải

Ví dụ 1: Một chiếc xe tăng tốc đều từ 18,5 m/s lên 46,1 m/s trong vòng 2,37 giây. Gia tốc trung bình của nó là bao nhiêu?

Viết phương trình: a = Δv / Δt = (vf – vi)/(tf – ti)

Xác định các biến: vf = 46,1 m/s, vi = 18,5 m/s, tf = 2,47 s, ti = 0 s.

Giải: a = (46,1 – 18,5)/2,47 = 11,17 m/s2.

Ví dụ 2: Một người đi mô-tô đang di chuyển với tốc độ 22,4 m/s thì đạp thắng và dừng lại sau 2,55 s. Tìm gia tốc của người đó.

Viết phương trình: a = Δv / Δt = (vf – vi)/(tf – ti)

Xác định các biến: vf = 0 m/s, vi = 22,4 m/s, tf = 2,55 s, ti = 0 s.

Giải: a = (0 – 22,4)/2,55 = -8,78 m/s2.

Ví dụ 3: Một đoàn tàu bắt đầu chuyển động nhanh dần đều khi đi hết 1km thứ nhất thì v1 = 10m/s. Tính vận tốc v sau khi đi hết 2km

Quãng đường đầu: v2 – v02 = 2.a.s ⇒ a = 0,05 m/s2

Vận tốc sau: v12 – v02 = 2.a.s’ ⇒ v12 – 0 = 2.0,05.2000 ⇒ v1 = 10√2 m/s

Ví dụ 5: Một chiếc canô chạy với v = 16 m/s, a = 2 m/s2 cho đến khi đạt được v = 24 m/s thì bắt đầu giảm tốc độ cho đến khi dừng hẳn. Biết canô từ lúc bắt đầu tăng vận tốc cho đến khi dừng hẳn là 10s. Hỏi quãng đường canô đã chạy.

Hướng dẫn:

Thời gian cano tăng tốc là:

Từ công thức: v = v0 + at1⇔ 24 = 16 + 2.t1 ⇒ t1 = 4s

Vậy thời gian giảm tốc độ: t2 = t – t1 = 6s

Quãng đường đi được khi tăng tốc độ:

Công thức tính gia tốc hướng tâm?

Bài tập ví dụ về gia tốc hướng tâm:

Ví dụ 1:

Một vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất trên một quỹ đạo có tâm là tâm Trái Đất và có bán kính 7000 km. Tốc độ dài của vệ tinh là 7,57 km/s. Tính gia tốc hướng tâm của vệ tinh.

Giải:

Xem thêm

Gia sư vật lý

Công thức tính áp suất chất lỏng

Công thức tính gia tốc

Công thức ma sát trượt