Công Thức Tính Nhanh động Học Chất điểm (chuẩn)

CÔNG THỨC TÍNH NHANH  ĐỘNG HỌC CHẤT ĐIỂM (CHUẨN)

I. Chuyển động thẳng đều:

    1. Vận tốc trung bình

    a.  Trường hợp tổng quát: \(v_{tb}=\frac{S}{t}\)

    b. Công thức khác: \(v_{tb}=\frac{v_{1}t_{1}+v_{2}t_{2}+...+v_{n}t_{n}}{t_{1}+t_{2}+...+t_{n}}\)

    c. Một số bài toán thường gặp:

Bài toán 1: Vật chuyển động trên một đoạn đường thẳng từ địa điểm A đến địa điểm B phải mất khoảng thời gian t. vận tốc của  vật trong nửa đầu của khoảng thời gian này là v1 trong nửa cuối là  v2. vận tốc trung bình  cả đoạn đường AB: \(v_{tb}=\frac{v_{1}+v_{2}}{2}\)

Bài toán 2: Một vật  chuyển động thẳng đều, đi một nửa quãng đường đầu với vận tốc v1, nửa quãng đường còn lại với vận tốc v2  Vận tốc trung  bình trên cả quãng đường: \(v=\frac{2v_{1}v_{2}}{v_{1}+v_{2}}\) 

    2. Phương trình chuyển động của chuyển động thẳng đều:     x = x0 + v.t

Dấu của x0	Dấu của v
x0 > 0 Nếu tại thời điểm ban đầu chất điểm ở vị thí thuộc phần 0x x0 < 0 Nếu tại thời điểm ban đầu chất điểm ở vị thí thuộc phần 0x,  x0 = 0 Nếu tại thời điểm ban đầu chất điểm ở gốc toạ độ.	v > 0 Nếu  cùng chiều 0x v < 0 Nếu  ngược chiều 0x

3. Bài toán chuyển động của hai chất điểm trên cùng một phương:

    Xác định phương trình chuyển động của chất điểm 1:

x1 = x01 + v1.t (1)

    Xác định phương trình chuyển động của chất điểm 2:

x2 = x02 + v2.t (2)

    Lúc hai chất điểm gặp nhau x1 = x2  t thế t vào (1) hoặc (2) xác định được vị trí gặp nhau

     Khoảng cách giữa hai chất điểm tại thời điểm t: \(d=\begin{vmatrix} x_{01}-x_{02}+(v_{01}-v_{02})t \end{vmatrix}\)

II. Chuyển động thẳng biến đổi đều

1. Vận tốc:  v = v0  + at

2. Quãng đường: \(s=v_{0}t+\frac{at^{2}}{2}\)

3. Hệ thức liên hệ: \(v^{2}-{v_{0}}^{2}=2as\rightarrow v=\sqrt{{v_{0}}^{2}+2as}=\frac{v^{2}-{v_{0}}^{2}}{2a}\)

4. Phương trình chuyển động: \(x=x_{0}+v_{0}t+\frac{at^{2}}{2}\)

Chú ý: Chuyển động thẳng nhanh dần đều a.v > 0.; Chuyển động thẳng chậm dần đều a.v < 0

Dấu của x0	Dấu của v0 ; a
x0 > 0 Nếu tại thời điểm ban đầu chất điểm ở vị thí thuộc phần 0x x0 < 0 Nếu tại thời điểm ban đầu chất điểm ở vị thí thuộc phần 0x,  x0 = 0 Nếu tại thời điểm ban đầu chất điểm ở gốc toạ độ.	v0; a > 0 Nếu \(\overrightarrow{v},\overrightarrow{a}\) cùng chiều 0x v ; a < 0 Nếu \(\overrightarrow{v},\overrightarrow{a}\) ngược chiều 0x

   

5. Bài toán gặp nhau của chuyển động thẳng biến đổi đều:

    - Lập phương trình toạ độ của mỗi chuyển động : \(x_{1}=x_{01}+v_{01}t+\frac{a_{1}t^{2}}{2},x_{1}=x_{02}+v_{02}t+\frac{a_{2}t^{2}}{2}\)

    - Khi hai chuyển động gặp nhau: x1 = x2  Giải phương trình này để đưa ra các ẩn của bài toán.

     Khoảng cách giữa hai chất điểm tại thời điểm t: \(d=\begin{vmatrix} x_{1}-x_{2} \end{vmatrix}\)

6. Một số bài toán thường gặp:

Bài toán 1: Một vật chuyển động thẳng nhanh dần đều đi được những đoạn đường s1và s2  trong hai khoảng thời gian liên tiếp bằng nhau là  t. Xác định vận tốc đầu và gia tốc của vật.

    Giải hệ phương trình: 

 

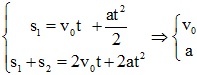
Bài toán 2: Một vật bắt đầu chuyển động thẳng nhanh dần đều. Sau khi đi được quãng đường s1 thì vật đạt vận tốc v1. Tính vận tốc của vật  khi đi được quãng đường s2  kể từ khi vật bắt đầu chuyển động.

\(v_{2}=v_{1}\sqrt{\frac{s_{2}}{s_{1}}}\)

Bài toán 3:Một vật bắt đầu chuyển động nhanh dần đều không vận tốc đầu:

    - Cho gia tốc a thì quãng đường vật đi được trong giây thứ n: \(\Delta s=na-\frac{a}{2}\)

    - Cho quãng đường vật đi được trong giây thứ n thì gia tốc xác định bởi: \(a=\frac{\Delta s}{n-\frac{1}{2}}\)   

Bài toán 4: Một vật đang chuyển động với vận tốc v0 thì chuyển động chầm dần đều:

    - Nếu cho gia tốc a thì quãng đường vật đi được cho đến khi dừng hẳn: \(s=\frac{-{v_{0}}^{2}}{2a}\)

    - Cho quãng đường vật đi được cho đến khi dừng hẳn s, thì gia tốc: \(a=\frac{-{v_{0}}^{2}}{2s}\)

    - Cho  a. thì thời gian chuyển động: t = \(\frac{-v_{0}}{a}\)

    - Nếu cho gia tốc a, quãng đường vật đi được trong giây cuối cùng: \(\Delta s=v_{0}+at-\frac{a}{2}\)

    - Nếu cho quãng đường vật đi được trong giây cuối cùng là \(\Delta s\), thì gia tốc : \(a=\frac{\Delta s}{t-\frac{1}{2}}\)

Bài toán 5: Một vật chuyển động thẳng biến đổi đều với gia tốc a, vận tốc ban đầu v0:

    - Vận tốc trung bình của vật từ thời điểm t1 đến thời điểm t2: \(v_{tb}=v_{0}+\frac{\left ( t_{1}+t_{2} \right )a}{2}\)

    - Quãng đường vật đi được từ thời điểm t1 đến thời điểm t2: \(s=v_{0}(t_{2}-t_{1})+\frac{\left ( t_{2}^{2}-t_{1}^{2} \right )a}{2}\)

Bài toán 6:  Hai xe chuyển động thẳng đều trên cùng 1 đường thẳng với các vận tốc không đổi. Nếu đi ngược chiều nhau, sau thời gian t khoảng cách giữa 2 xe giảm một lượng a.  Nếu đi cùng chiều nhau, sau thời gian t khoảng cách giữa 2 xe giảm một lượng b. Tìm vận tốc mỗi xe.       

Giải hệ phương trình:

 

III. Sự rơi tự do: Chọn gốc tọa độ tại vị trí rơi, chiều dương hướng xuông, gốc thời gian lúc vật bắt đầu rơi.

    1. Vận tốc rơi tại thời điểm t: v = gt.

    2. Quãng đường đi được của vật sau thời gian t: \(s=\frac{1}{2}gt\)

    3. Công thức liên hệ:  v2 = 2gs

    4. Phương trình chuyển động: \(y=\frac{1}{2}gt^{^{2}}\)

    4. Một số bài toán thường gặp:

Bài toán 1: Một vật rơi tự do từ độ cao h: 

    - Thời gian rơi xác định bởi: \(t=\sqrt{\frac{2h}{g}}\)

    - Vận tốc lúc chạm đất xác định bởi: \(v=\sqrt{2gh}\)

    - Quãng đường vật rơi trong giây cuối cùng: \(\Delta s=\sqrt{2gh}-\frac{g}{2}\)

Bài toán 2: Cho quãng đường vật rơi trong giây cuối cùng:

    -Thời gian rơi xác định bởi: \(t=\frac{\Delta s}{g}+\frac{1}{2}\)

    - Vận tốc lúc chạm đất: \(v=\Delta s+\frac{g}{2}\)

    - Độ cao từ đó vật rơi: \(h=\frac{g}{2}.\left ( \frac{\Delta s}{g} +\frac{1}{2}\right )^{2}\)

Bài toán 3: Một vật rơi tự do:

    - Vận tốc trung bình của chất điểm từ thời điểm t1 đến thời điểm t2: \(v_{tb}=\frac{(t_{1}+t_{2})g}{2}\)

    - Quãng đường vật rơi được từ thời điểm t1 đến thời điểm t2: \(s=\frac{(t_{2}^{2}-t_{1}^{2})g}{2}\)

IV. Chuyển động ném đứng  từ dưới lên từ mặt đất với vận tốc ban đầu v0: Chọn chiểu dương thẳng đứng hướng lên, gốc thời gian lúc ném vật.

    1. Vận tốc: v = v0 - gt

    2. Quãng đường: \(s=v_{0}t-\frac{gt^{2}}{2}\)

    3. Hệ thức liên hệ: \(v^{2}-v_{0}^{2}=-2gs\)

    4. Phương trình chuyển động: \(y=y_{0}t-\frac{gt^{2}}{2}\)

    5. Một số bài toán thường gặp:

Bài toán 1: Một vật được ném thẳng đứng lên cao từ mặt đất với vận tốc đầu v0 :

    - Độ cao cực đại mà vật lên tới: \(h_{max}=\frac{v_{0}^{2}}{2g}\)

    - Thời gian chuyển động của vật: \(t=\frac{2v_{0}}{g}\)

Bài toán 2: Một vật được ném thẳng đứng lên cao từ mặt đất . Độ cao cực đại mà vật lên tới là h max

    - Vận tốc ném: \(v_{0}=\sqrt{2gh_{max}}\)

    - Vận tốc của vật tại độ cao h1: \(v=\pm \sqrt{v_{0}^{2}-2gh_{1}}\)

V. Chuyển động ném đứng  từ dưới lên từ  độ cao h0  với vận tốc ban đầu v0 :

    Chọn gốc tọa độ tại mặt đất chiểu dương thẳng đứng hướng lên, gốc thời gian lúc ném vật.

    1. Vận tốc: v = v0 - gt

    2. Quãng đường: \(s=v_{0}t-\frac{gt^{2}}{2}\)

    3. Hệ thức liên hệ: \(v^{2}-v_{0}^{2}=-2gs\)

    4. Phương trình chuyển động: \(y=h_{0}+v_{0}t-\frac{gt^{2}}{2}\)

    5. Một số bài toán thường gặp:

Bài toán 1: Một vật ở độ cao h0 được ném thẳng đứng lên cao với vận tốc đầu v0 :

    - Độ cao cực đại mà vật lên tới: \(h_{max}=h_{0}+\frac{v_{0}^{2}}{2g}\)

    -  Độ lớn vận tốc lúc chạm đất: \(v=\sqrt{v_{0}^{2}+2gh_{0}}\)

    - Thời gian chuyển động: \(t=\frac{\sqrt{v_{0}^{2}+2gh_{0}}}{g}\)       

Bài toán 2: Một vật ở độ cao h0 được ném thẳng đứng lên cao. Độ cao cực đại mà vật lên tới là hmax :

    - Vận tốc ném: \(v_{0}=\sqrt{2g(h_{max}-h_{0})}\)

    - Vận tốc của vật tại độ cao h1: \(v=\pm \sqrt{v_{0}^{2}+2g(h_{0}-h_{1})}\)

    - Nếu bài toán chưa cho h0 , cho  v0 và hmax thì: \(h_{0}=h_{m_{ax}}-\frac{v_{0}^{2}}{2g}\) 

VI. Chuyển động ném đứng từ trên xuống : Chọn gốc tọa độ tại vị trí ném ; chiểu dương thẳng đứng hướng vuống, gốc thời gian lúc ném vật.

    1. Vận tốc: v = v0 + gt

    2. Quãng đường: \(s=v_{0}t+\frac{gt}{2}\)

    3. Hệ thức liên hệ: \(v^{2}-v_{0}^{2}=2gs\)

    4. Phương trình chuyển động: \(y=y_{0}+\frac{gt^{2}}{2}\)

    5. Một số bài toán thường gặp:

Bài toán 1: Một vật ở độ cao h được ném thẳng đứng hướng xuống với vận tốc đầu v0:

    - Vận tốc lúc chạm đất: \(v_{max}=\sqrt{v_{0}^{2}+2gh}\)

    - Thời gian chuyển động của vật: \(t=\frac{\sqrt{v_{0}^{2}+2gh-v_{0}}}{g}\)

    - Vận tốc của vật tại độ cao h1: \(v=\sqrt{v_{0}^{2}+2g(h-h_{1})}\)