Công Thức Vật Lý 12 ( Cô đọng, đầy đủ)

CÔNG THỨC VẬT LÝ 12

DAO ĐỘNG ĐIỀU HÒA

* Chọn gốc tọa độ tại vị trí cân bằng: 

- Phương trình dao động: \(x=Acos\left ( \omega t+\varphi \right )\)

- Phương trình vận tốc: v = \(-\omega Asin(\omega t+\varphi )\)

- Phương trình gia tốc: \(a=-\omega ^{2}cos(\omega t+\varphi )=-\omega ^{2}x\)

( x: li độ dao động, A: biên độ dao động, \(\varphi\): pha ban đầu (rad), \(\omega\): tần số góc(rad/s) )

* Các giá trị cực đại: \(x_{max}=A\), \(v_{max}=A\omega\) (tại VTCB), \(a_{max}=A\omega ^{2}\) (tại biên)

* Hệ thức độc lập

- \(A^{2}=x^{2}+\frac{v^{2}}{\omega ^{2}}\)

- \(A^{2}=\frac{a^{2}}{\omega ^{4}}+\frac{v^{2}}{\omega ^{2}}\) \(\rightarrow v=\pm \omega \sqrt{A^{2}-x^{2}}\)

+ Tại ví trí cân bằng: x = 0, \(v_{max}=\omega A\), a = 0

+ Tại biên: \(x_{max}=A\), v = 0, \(a_{max}=\omega ^{2}A\)

+ Tốc độ trung bình trong 1 chu kỳ: \(\overline{v}=\frac{4A}{T}\)

+ Liên hệ về pha:  v sớm pha \(\frac{\pi }{2}\) hơn x, a sớm pha \(\frac{\pi }{2}\) hơn v, a ngược pha với x

CON LẮC LÒ XO

- Tần số góc: \(\omega =\sqrt{\frac{k}{m}}\rightarrow k=m\omega ^{2}(\omega =2\pi f)\)

- Chu kì: T = \(\frac{2\pi }{\omega }=2\pi \frac{k}{m}\)

- Tần số: \(f=\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\)

* Nếu \(m_{1}=m_{1}+m_{2}\) \(\rightarrow T^{2}=T_{1}^{2}+T_{2}^{2}\)

* Nếu \(m_{1}=m_{1}-m_{2}\) \(\rightarrow T^{2}=T_{1}^{2}-T_{2}^{2}\)

- Lập phương trình dao động điều hòa:

Phương trình có dạng: \(x=Acos\left ( \omega t+\varphi \right )\)

+ Tìm \(\omega\): \(\omega =\sqrt{\frac{k}{m}}=\frac{2\pi }{T}=2\pi f...\) 

+ Tìm A: \(A^{2}=\frac{a^{2}}{\omega ^{4}}+\frac{v^{2}}{\omega ^{2}}\), l = 2A, \(v_{max}=A\omega ...\)

+ Tìm \(\varphi\): Chọn t = 0 lúc vật qua vị trí \(x_{0}\): \(x_{0}=Acos\varphi\Rightarrow cos\varphi =\frac{x_{0}}{A}=cos\phi \Rightarrow \left\{\begin{matrix} \varphi =\theta \\ \varphi =-\phi \end{matrix}\right.\)

- Năng lượng dao động điều hòa: 

+ Động năng: \(W_{d}=\frac{mv^{2}}{2}=\frac{kA^{2}}{2}sin^{2}(\omega t+\varphi )\)

+ Thế năng: \(W_{t}=\frac{kx^{2}}{2}=\frac{kA^{2}}{2}cos^{2}(\omega t+\varphi )\)

+ Cơ năng: \(W=W_{d}+W_{t}=\) hằng số, \(W=\frac{kA^{2}}{2}=\frac{{m\omega ^{2}A^{2}}}{2}=\frac{mv_{max}^{2}}{2}\)

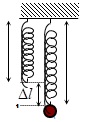
- Con lắc lò xo treo thẳng đứng:

Gọi \(l_{0}\): chiều dài tự nhiên của lò xo, \(\Delta l\): độ dãn của lò xo khi vật ở VTCB, \(l_{b}\): chiều dài khi vật ở VTCB.

\(\Rightarrow l_{b}=l_{0}+\Delta l\)

* Khi vật ở VTCB: \(F_{dh}=P\rightarrow k\Delta l=mg\)

.............................................................................................................................................................................

PHẢN ỨNG HẠT NHÂN

* Trong phản ứng hạt nhân: \(_{Z_{1}}^{A_{1}}\textrm{X1}+_{Z_{2}}^{A_{2}}\textrm{X2}\rightarrow _{Z_{3}}^{A_{3}}\textrm{X3}+_{Z_{4}}^{A_{4}}\textrm{X4}\)

- Bảo toàn số nuclon: \(A_{1}+A_{2}= A_{3}+A_{4}\)

- Bảo toànsố điện tích: \(Z_{1}+Z_{2}=Z_{3}+Z_{4}\)

- Năng lượng tỏa ra hoặc thu vào trong phản ứng hạt nhân: 

 \(\Delta E=(m_{1}+m_{2}-m_{3}-m_{4})c^{2}=(m_{1}+m_{2}-m_{3}-m_{4}).931,5MeV\)

 \(\Delta E=(\Delta m_{3}+\Delta m_{4}-\Delta m_{1}-\Delta m_{2})c^{2}\)

 \(\Delta E=K_{4}+K_{3}-K_{2}-K_{1}\)

+ Nếu m1 + m2> m3 + m4ΔE> 0 thì phản ứng hạt nhân tỏa năng lượng.

+ Nếu m1 + m2< m3 + m4ΔE< 0thì phản ứng hạt nhân thu năng lượng.

* Đơn vị khối lượng nguyên tử: 1u = 931,5\(\frac{MeV}{c^{2}}\), 1MeV = 1,6.10-13 J

* Động lượng: \(\overrightarrow{P_{1}}+\overrightarrow{P_{2}}= \overrightarrow{P_{3}}+\overrightarrow{P_{4}}\)

- Động lượng trọng phóng xạ: \(P_{\alpha }=P_{con}\)

- Liên hệ động năng: \(p^{2}=2mK\)

* Thuyết tương đối hẹp anhxtanh: \(mc^{2}=m_{0}c^{2}+K\)

- Năng lượng tương đối: \(E= m_{0}c^{2}+\frac{m_{0}c^{2}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\)

- Khối lượng tương đối: \(m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\)

- Động năng tương đối: \(K=W_{d}=m_{0}\left ( \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} -1\right )\)