Dải Mobius Là Gì? Những Điều Kỳ Diệu Về Dải Mobius

• Trang chủ
• Diễn đàn Bài viết mới Tìm kiếm
• Tin mới Nổi bật Bài viết mới Nhật ký mới Hoạt động
• Tiện ích Up ảnh miễn phí Kiểm tra chính tả Kiếm tiền Online Mua bitcoin làm giàu Thẻ điện thoại miễn phí
• Thành viên Đã đăng ký Đang truy cập Nhật ký mới Tìm kiếm
• Danh bạ New items New comments Latest reviews Tìm kiếm danh bạ Mark read

Đăng nhập Đăng ký Trực tiếp Tìm kiếm

Tìm kiếm

Mọi nơi Đề tài thảo luận Diễn đàn này This thread Chỉ tìm trong tiêu đề Note Bởi: Tìm kiếm Tìm nâng cao…

• Bài viết mới
• Tìm kiếm

Danh mục Đăng nhập Đăng ký Install the app Install How to install the app on iOS

Follow along with the video below to see how to install our site as a web app on your home screen.

Note: This feature may not be available in some browsers.

You are using an out of date browser. It may not display this or other websites correctly.You should upgrade or use an alternative browser.

• Thread starter Thread starter Swaka Nguyệt Lam
• Ngày gửi Ngày gửi 22 Tháng bảy 2021

• Trang chủ
• Diễn đàn
• E - CÁC CÂU LẠC BỘ
• CLB Học Tập
• Khoa Học

• Tặng tiền điện tử miễn phí
• Phát thẻ điện thoại miễn phí
• Những nhiệm vụ kiếm tiền
• Hướng dẫn kiếm tiền Binance

Đặt quảng cáo Binance kiếm tiền thông báo chơi game 2048 text link facebook cách viết bài thẻ điện thoại BOT giao dịch MEXC tự sướng 5 triệu Dải Mobius là gì? Những điều kỳ diệu về dải Mobius [Xóa] 1 người đang xem Theo dõi S

Swaka Nguyệt Lam

Giai Nguyệt Lam

Xu 39,211 16,603 ❤︎ Bài viết: 695 Kiếm tiền Swaka Nguyệt Lam đã kiếm được 27430 đ Dải Mobius là gì? Bạn rất có thể đã bắt gặp những đồ vật một mặt hàng trăm lần trong cuộc sống hàng ngày của mình - như biểu tượng phổ quát về tái chế, được in trên mặt sau của lon nhôm và chai nhựa. ​ Đối tượng toán học này được gọi là dải Mobius. Nó đã thu hút các nhà môi trường học, nghệ sĩ, kỹ sư, nhà toán học và nhiều người khác kể từ khi được phát hiện vào năm 1858 bởi August Möbius, một nhà toán học người Đức đã qua đời 150 năm trước, vào ngày 26 tháng 9 năm 1868. Möbius phát hiện ra dải một mặt vào năm 1858 khi đang là chủ nhiệm bộ môn thiên văn học và cơ học cao hơn tại Đại học Leipzig. (Một nhà toán học khác tên là Listing thực sự đã mô tả nó vài tháng trước đó, nhưng không công bố công trình của mình cho đến năm 1861) Möbius dường như đã gặp dải Mobius trong khi nghiên cứu lý thuyết hình học của khối đa diện, các hình đặc bao gồm các đỉnh, các cạnh và mặt phẳng. Có thể tạo dải Mobius bằng cách lấy một dải giấy, tạo cho nó một số nửa xoắn lẻ, sau đó dán các đầu lại với nhau để tạo thành một vòng. Nếu bạn lấy bút chì và vẽ một đường dọc theo tâm của dải, bạn sẽ thấy rằng đường dường như chạy dọc theo cả hai bên của vòng lặp. Khái niệm về một vật thể một mặt đã truyền cảm hứng cho các nghệ sĩ như nhà thiết kế đồ họa người Hà Lan M. C. Escher, người có bức tranh khắc gỗ "Möbius Strip II" cho thấy những con kiến đỏ đang bò lần lượt dọc theo dải Mobius. Dải Mobius có nhiều hơn một đặc tính đáng ngạc nhiên. Ví dụ, hãy thử lấy một chiếc kéo và cắt dải giấy làm đôi dọc theo đường bạn vừa vẽ. Bạn có thể ngạc nhiên khi thấy rằng bạn thu được hai dải Mobius một mặt nhỏ hơn, mà thay vào đó là một dải dài hai mặt. Nếu bạn không có một mảnh giấy trong tay, bức tranh khắc gỗ "Möbius Strip I" của Escher cho thấy điều gì sẽ xảy ra khi một dải Mobius bị cắt dọc theo đường chính giữa của nó. 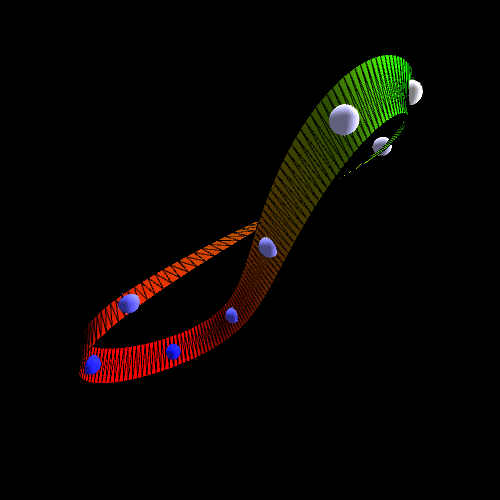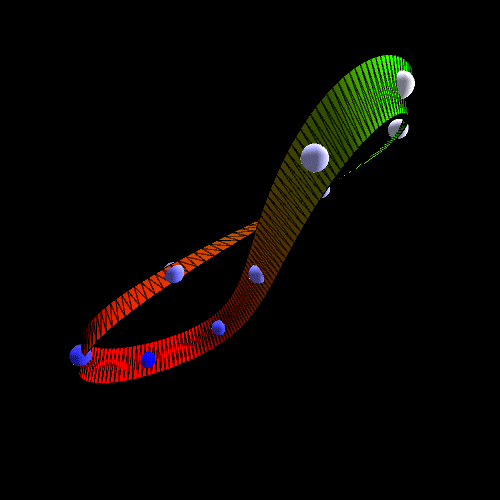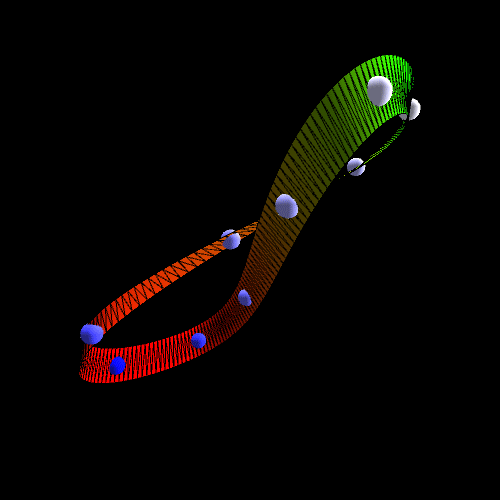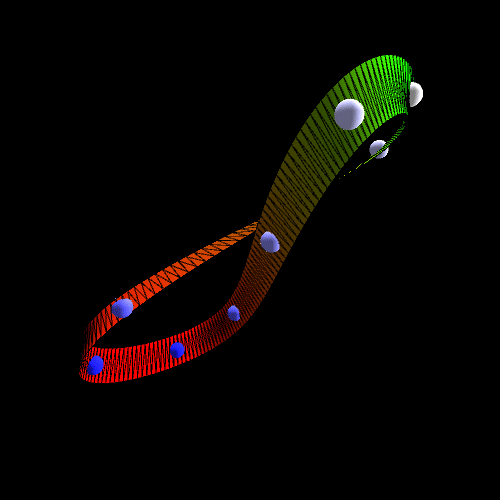Mặc dù dải này chắc chắn có sức hấp dẫn trực quan, nhưng tác động lớn nhất của nó là trong toán học, nơi nó đã giúp thúc đẩy sự phát triển của toàn bộ lĩnh vực được gọi là cấu trúc liên kết. Một nhà cấu trúc học nghiên cứu các đặc tính của các đối tượng được bảo toàn khi di chuyển, uốn cong, kéo căng hoặc xoắn, mà không cần cắt hoặc dán các bộ phận lại với nhau. Ví dụ: Một cặp tai nghe bị rối theo nghĩa cấu trúc liên kết giống như một cặp tai nghe không bị rối, bởi vì việc thay đổi một cặp tai nghe khác chỉ cần di chuyển, uốn cong và xoắn. Không cần cắt hoặc dán để chuyển đổi giữa chúng. Một cặp vật thể khác giống nhau về mặt cấu trúc là một tách cà phê và một chiếc bánh rán. Bởi vì cả hai vật chỉ có một lỗ, một vật có thể bị biến dạng thành vật kia chỉ bằng cách kéo căng và uốn cong. Số lượng lỗ trên một vật thể là một thuộc tính chỉ có thể thay đổi thông qua việc cắt hoặc dán. Thuộc tính này - được gọi là "chi" của một vật thể - cho phép chúng ta nói rằng một cặp tai nghe và một chiếc bánh donut khác nhau về mặt cấu trúc, vì một chiếc bánh donut có một lỗ, trong khi một cặp tai nghe không có lỗ. Thật không may, một dải Mobius và một vòng lặp hai mặt, giống như một dây đeo cổ tay silicone điển hình, dường như đều có một lỗ, vì vậy đặc tính này không đủ để phân biệt chúng - ít nhất là theo quan điểm của một nhà cấu trúc học. Thay vào đó, đặc tính phân biệt dải Mobius với vòng hai mặt được gọi là khả năng định hướng. Giống như số lượng lỗ, khả năng định hướng của vật thể chỉ có thể được thay đổi thông qua việc cắt hoặc dán. Hãy tưởng tượng bạn đang viết một ghi chú trên một bề mặt có thể nhìn xuyên qua, sau đó đi dạo một vòng trên bề mặt đó. Bề mặt có thể định hướng được nếu khi bạn đi bộ về, bạn luôn có thể đọc được ghi chú. Trên một bề mặt dễ nhận biết, bạn có thể quay lại sau chuyến đi bộ của mình chỉ để thấy rằng những từ bạn viết dường như đã biến thành hình ảnh phản chiếu của chúng và chỉ có thể đọc từ phải sang trái. Trên vòng lặp hai mặt, ghi chú sẽ luôn đọc từ trái sang phải, bất kể hành trình của bạn đã đưa bạn đến đâu. Vì dải Mobius là không thể đi qua, trong khi vòng lặp hai mặt có thể định hướng được, điều đó có nghĩa là dải Mobius và vòng lặp hai mặt khác nhau về mặt cấu trúc. ​ Khái niệm về khả năng định hướng có ý nghĩa quan trọng. Lấy chất đối quang. Các hợp chất hóa học này có cấu trúc hóa học giống nhau ngoại trừ một điểm khác biệt chính: Chúng là hình ảnh phản chiếu của nhau. Ví dụ, hóa chất L-methamphetamine là một thành phần trong Vicks Vapor Inhalers. Hình ảnh phản chiếu của nó, D-methamphetamine, là một loại ma túy bất hợp pháp loại A. Nếu chúng ta sống trong một thế giới không ai biết đến, những hóa chất này sẽ không thể phân biệt được. Khám phá của August Möbius đã mở ra những cách mới để nghiên cứu thế giới tự nhiên. Nghiên cứu về cấu trúc liên kết tiếp tục tạo ra những kết quả đáng kinh ngạc. Ví dụ, năm ngoái, cấu trúc liên kết đã dẫn dắt các nhà khoa học khám phá ra những trạng thái mới lạ của vật chất. Huy chương Fields năm ấy, danh hiệu cao quý nhất trong toán học, được trao cho Akshay Venkatesh, một nhà toán học đã giúp tích hợp cấu trúc liên kết với các lĩnh vực khác như lý thuyết số. Chỉnh sửa cuối: 23 Tháng bảy 2021 Từ khóa: Sửa

• Từ khóa Từ khóa kiến thức kiến thức cuộc sống kiến thức khoa học

Những người đang xem chủ đề này

Tổng: 2 Thành viên: 0, Khách: 2

Các chủ đề tương tự

Review Truyện [Manhwa] Dải Hợp Âm Trên Đại Dương Xanh - Wwa100

• BonggMi
• 5 Tháng tám 2023
• Sách - Truyện

Trả lời 0 Đọc 2K 5 Tháng tám 2023 BonggMi S Đọc hiểu Chợ tết: Dải mây trắng đỏ dần trên đỉnh núi - Đoàn Văn Cừ

• Swaka Nguyệt Lam
• 14 Tháng tư 2023
• Học Online

Trả lời 0 Đọc 7K 14 Tháng tư 2023 Swaka Nguyệt Lam S [Lyrics + Vietsub] Dành Tặng Anh Cả Dải Ngân Hà - Ycccc

• Nhiên Trần
• 2 Tháng mười 2022
• Quốc Tế

Trả lời 0 Đọc 1K 2 Tháng mười 2022 Nhiên Trần T Review Phim Movie 35: Nobita Và Đội Vệ Binh Dải Ngân Hà

• Thomas
• 27 Tháng bảy 2022
• Cần Sửa Bài

Trả lời 0 Đọc 1K 27 Tháng bảy 2022 Thomas T Đọc hiểu: Dải đồng bằng thương nhớ - Đoàn Tuấn

• Thùy Minh
• 30 Tháng năm 2022
• Học Online

Trả lời 3 Đọc 22K 14 Tháng mười hai 2024 Thùy Minh Share: Facebook X Bluesky LinkedIn Reddit Tumblr Email Share Link

Nội dung nổi bật

• Hướng dẫn kiếm tiền từ việc đăng ảnh
  • Admin
  • 25 Tháng ba 2019
  Trả lời: 1
• Các nhiệm vụ kiếm tiền online tại diễn đàn
  • Admin
  • 18 Tháng tư 2018
  Trả lời: 17
• Giới thiệu thành viên - Kiếm tiền không giới hạn
  • Admin
  • 16 Tháng tư 2018
  Trả lời: 9
• Hướng dẫn cách kiếm nhiều xu từ việc giới thiệu bạn bè
  • Admin
  • 31 Tháng bảy 2019
  Trả lời: 40
• Hướng dẫn cách chia sẻ bài viết lên Facebook, Twitter kiếm tiền
  • Admin
  • 26 Tháng mười một 2015
  Trả lời: 1

Xu hướng nội dung

• M [Dịch] Tuyệt Thế Binh Vương - Tiêu Thần Tô Tình - Vũ Công Cô Đơn
  • mrgu21
  • 5 Tháng sáu 2025
  Trả lời: 5K
• Nối chữ tiếng Việt
  • luuxinh69
  • 16 Tháng tám 2020
  Trả lời: 5K
• Nối chữ tiếng Anh
  • Xuân Lê
  • 24 Tháng mười một 2020
  Trả lời: 4K
• Trò chơi Tìm từ ba chân
  • Wall-E
  • 26 Tháng tư 2018
  Trả lời: 2K
• Nối từ tiếng Việt online
  • Muối
  • 29 Tháng tư 2018
  Trả lời: 2K

Chia sẻ trang này

Facebook X Bluesky LinkedIn Reddit Tumblr Email Share Link

• Trang chủ
• Diễn đàn
• E - CÁC CÂU LẠC BỘ
• CLB Học Tập
• Khoa Học

• Tuyển QTV phát triển diễn đàn

Back