[THTT] Dải Băng Kỳ Diệu Mobius Và Những Nghịch Lý Trong Cuộc ...

Góp ý và báo lỗi cho YBOX tại đây

Thao Tran

~100.000 followers

Theo dõi Nhắn tin

Thông tin

• Đang cập nhật...
• Đang cập nhật...
• Đang cập nhật... ~ 100.000 người

Sở thích

Chưa có thông tin

Cần tim bạn

Chưa có thông tin

• Đang cập nhật...

Thao Tran@Triết Học Tuổi Trẻ

8 năm trước

[THTT] Dải Băng Kỳ Diệu Mobius Và Những Nghịch Lý Trong Cuộc Sống

Mặt mobius hay dải băng mobius về toán học là một khái niệm topo cơ bản về một dải chỉ có một phía và một biên. Vậy thì cái lý thuyết toán học mang tính chất hàn lâm này nó ảnh hưởng gì đến đời sống của chúng ta? Nếu bạn thấy chả có gì “thú vị” với cái lý thuyết ngớ ngẩn này thì chắc chắn bạn đã lầm to rồi, vì tôi sẽ cho bạn thấy những nghịch lý trong cuộc sống của chúng ta gắn liền với cái dải băng “xoắn não” này.

Mặt mobius được đặt theo tên một nhà toán học và thiên văn học người Đức August Ferdinand Möbius, ông đã phát hiện ra dải băng này năm 1853. Ta có thể tạo một dải băng Mobius đơn giản bằng cách lấy một băng giấy dài chữ nhật, lật ngược một đầu băng giấy và nối vào đầu kia - trong toán học gọi là mặt Mobius một mặt nghiêng và một biên. Tùy vào chiều xoay mà ta có 2 loại mặt Mobius: mặt Mobius thuận chiều và ngược chiều kim đồng hồ. Lúc đầu chỉ như một trò chơi vì xuất xứ từ một dải băng giấy (do Mobius công bố) được dán dính hai đầu sau khi lật ngược một đầu từ 1 đến 2 lần, về sau trở thành công thức toán và được áp dụng rất nhiều lĩnh vực trong đời sống. Nếu đọc đến đây bạn vẫn chưa tài nào hiểu được những gì tôi muốn đề cập thì cứ bình tĩnh và đọc tiếp bạn sẽ chiêm nghiệm ra được thôi.

1. Từ số nguyên tố Palindrome đến bản nhạc Bach

Trong toán học, số nguyên tố Palindrome hay số xuôi ngược nguyên tố là số nguyên tố viết xuôi viết ngược chỉ cho ra một số. Lấy ví dụ cụ thể như sau: 11411,15551,…

Trong âm nhạc có một bản nhạc tương tự có tên là bản nhạc canon con cua do thiên tài âm nhạc J.S. Bach sáng tác vào khoảng giữa thế kỷ thứ 18. Bản nhạc này là do 2 tay chơi, một tay chơi các nốt ở dòng trên và một tay chơi các nốt ở dòng dưới. Nhưng khi chơi tới cuối bài, thì thấy một điều là phần cuối của dòng trên trùng với phần đầu của dòng dưới, và phần cuối của dòng dưới trùng với phần đầu của dòng trên. Tức là bản nhạc này có sự đối xứng giữa đầu và đuôi như một palindrome.

2. Phép ẩn dụ trong dải băng mobius

Phép ẩn dụ trong dải băng mobius được mô tả thông qua nhận thức của người thứ nhất và người thứ ba.Nhận thức của một người có thể thay đổi và khi bị thay đổi nó sẽ không thể trở lại nguyên bản nữa bởi vì nó sẽ có sự xuất hiện của nhân tố tác động đến sự thay đổi đó. Đơn giản dễ hiểu là một khi nhận thức của bạn bị một đối tượng khác tác động thì nó sẽ không thể như ban đầu được nữa và bạn sẽ thực hiện lại điều đó với một đối tượng khác trong hoàn cảnh tương tự. Giống như trong một mối quan hệ, nhận thức của chúng ta giữ vai trò quan trọng trong cách chúng ta thể hiện bản thân với người khác và cách chúng ta đối xử với đối phương.

Tương tự như dải băng mobius, đối với các mối quan hệ trong quá khứ của chúng ta đều có tác động đến các mối quan hệ hiện tại và tương lai của chúng ta. Có nghĩa là chúng ta sẽ vô hình chung đối xử với người thứ ba giống như cách người thứ nhất đã từng đối xử với chúng ta. Nếu một người có sự áp đặt, tác động đến tư tưởng của chúng ta và thay đổi quan điểm lẫn thế giới quan của chúng ta thì chúng ta sẽ có xu hướng thực hiện điều đó tương tự với người khác. Cho một ví dụ dễ hiểu trong cuộc sống, nếu một thanh niên từ nhỏ hay bị bố đánh đập tàn nhẫn vì cho rằng đó mới là dạy dỗ chúng và tương lai khi thanh niên này lớn lên cũng ở vị trí tương tự đó bỗng nhiên anh ta cũng tỏ thái độ y hệt bố của anh ta lúc trước và đánh đập con cái mình. Lý giải này giúp các bạn phần nào dễ hiểu hơn nhiều rồi phải không? Nó để lại ấn tượng mạnh mẽ và sâu đậm trong tiềm thức khi họ hồi tưởng về những sự việc tương tự đã từng xảy ra, nó như một vết sẹo không thể nhìn thấy bằng mắt thường nhưng luôn chảy liền mạch trong suy nghĩ của họ một cách vô thức bào mòn đi lý trí con người. Đừng vô tình làm tổn thương người khác bởi những việc bạn đã từng bị người khác đối xử giống vậy. Bạn thất bại trong tình cảm, bị người khác phản bội không có nghĩa những người khác đều xấu như vậy.

3. Nghịch lý “đúng”, “sai”

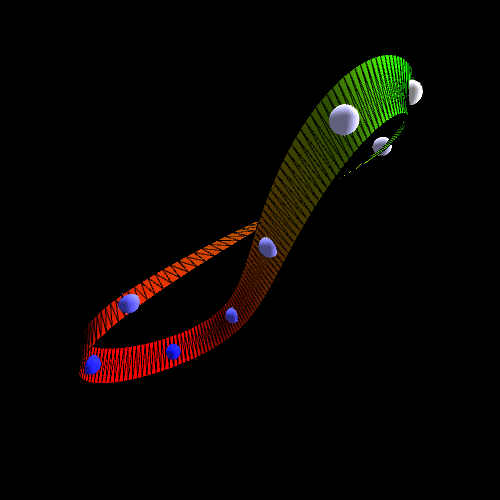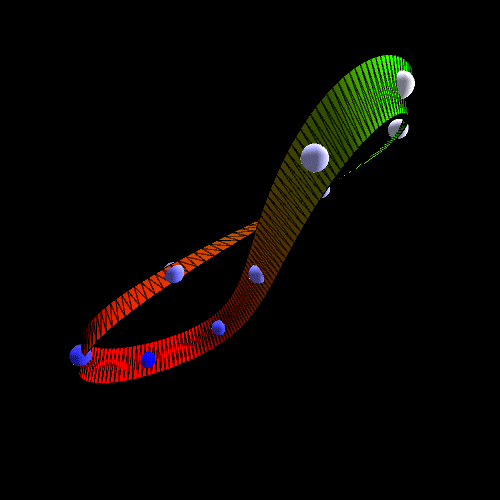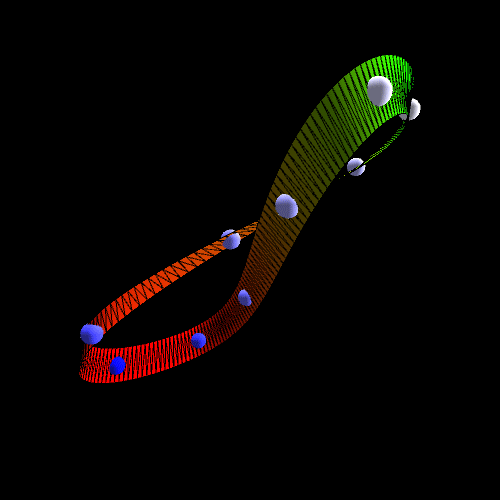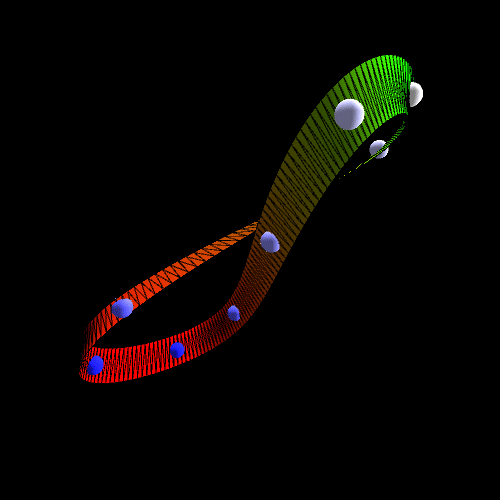
Nếu ta hình dung có một con kiến bò trên dải băng Mobius này (theo hướng quay vòng, chứ không bò ra biên), thì một lúc sau nó sẽ thành bị “lộn đầu”, tức là bò ở mặt bên kia của dải băng ! Nói cách khác, thay vì có hai mặt như là dải băng bình thường, dải băng này chỉ có 1 mặt thôi ! Tính chất này trong toán học gọi là tính “không định hướng được” (non-orientable), có nghĩa là không thể gọi đâu là mặt trên đâu là mặt dưới được.

Nếu chúng ta gọi một mặt của dải mobius là “đúng” còn dải biên là “sai” ta sẽ thấy một điều khá thú vị xảy ra: Khi chúng ta đi vòng quanh chúng ta sẽ thấy mình đang đi xen kẽ giữa “đúng” và “sai”. Điều này dẫn đến một nghịch lý khác nếu chúng ta gọi một bên là “I=1” và phía bên kia là “I=-1” đi lòng vòng chúng ta lật qua lật lại giữa 1/-1, có một phương trình “I=-1/I” nếu I có giá trị là 1 thì -1/1 là -1 vì vậy “I=-1”, tương tự nếu I có giá trị là -1 thì -1/-1 là “I=1”. Trở lại với nghịch lý “đúng”,”sai” ở phía trên, ta sẽ có hai trường hợp xảy ra như sau.

+ Nếu ta đi theo lộ trình “rời rạc” tức là lật mặt của vấn đề như lật bánh tráng ấy giống ở ví dụ phương trình I chúng ta sẽ thấy sự thay đổi rõ rệt về cách nhìn nhận “đúng” và “sai”.

+ Nhưng nếu chúng ta đi theo lộ trình “liên tục” thì ta sẽ thấy sự song hành của cả hai mặt “đúng” và “sai”.

Do đó tuy nghe có vẻ “nghịch lý” nhưng thực chất chúng có tính nhất quán với nhau. Hơn nữa nếu bạn chấm một điểm ở mặt “đúng”, khi bạn đi ở mặt “sai” bạn vẫn sẽ thấy cái điểm “đúng” ở phía bên kia, giống hình thái cực đồ âm dương trong văn hóa phương Đông, dù bạn đi theo lộ trình nào thì nghịch lý “đúng”, “sai” kia vẫn luôn tồn tại như một điều hiển nhiên trong chiều sâu vô thức. Mọi sự việc trong cuộc sống của chúng ta nghe có vẻ đối lập nhưng thực chất chúng luôn tồn tại song hành, chỉ khác ở cách thức bạn nhìn nhận một vấn đề mà thôi. Bạn nhìn nhận nó “đúng” nhưng chưa chắc nó đã “đúng” hoàn toàn như bạn nghĩ, bạn thấy điều đó có vẻ “sai” nhưng không hẳn nó hoàn toàn “sai”. Về mọi phương diện, bạn nên đặt bản thân ở vị trí thứ ba để có cái nhìn tổng thể toàn bộ sự việc, dù đúng dù sai vẫn nằm ở sự lựa chọn.

4.Biểu tượng vô cực “infinity” và vòng lặp không hồi kết

Nếu ta lấy dải băng bình thường, rồi lấy kéo cắt theo đường giữa (cách đều 2 bên mép của dải băng), thì thành được 2 dải băng. Thế nhưng, nếu lấy dải băng Mobius mà cắt theo đường giữa như vậy, thì vẫn chỉ được 1 dải băng thôi, có điều nó dài gấp đôi dải cũ! Bạn thử lấy giấy dán thành dải băng vòng tròn “lộn đầu đuôi” Bach-Mobius rồi cắt ở giữa mà xem ? Sau khi đã nhìn tận mắt thấy đúng là cắt đôi vẫn ra chỉ 1 dải rồi, thì thử giải thích vì sao lại vậy ?

Biểu tượng vô cực trong toán học biểu hiện sự vô tận trong cái tận cùng mà bạn chẳng biết là bạn đang đi đâu nữa. Điều này minh chứng rõ ràng cho việc khi bạn đào sâu tìm hiểu một vấn đề thì bạn càng gặp rắc rối do chính bạn tạo ra, không những không sáng tỏ mà nó còn càng biến chất so với ban đầu. Nghe có vẻ kinh khủng nhỉ, nhưng đó là sự thật, giống như ví dụ về đàn kiến ở phía trên tôi có đề cập. Khi bạn đang đi ở xuất phát điểm này bạn thấy mọi người đang đi hướng ngược lại phía bên kia, bạn hoang mang cố gắng chạy thật nhanh để theo kịp người khác nhưng rồi bạn không nhận ra rằng cái vị trí hiện tại bạn đang đứng cũng chính là cái vị trí người khác đã từng đi qua rồi. Cứ yên tâm và an ủi bản thân bạn là chúng ta ai cũng ở trong cái vòng lặp đó và không ai thoát được cả đâu, việc bạn cần làm là cứ bình tĩnh và luôn giữ tâm trí ổn định, tinh thần thật sáng suốt thông tuệ nếu bạn không muốn là đứa mãi chạy theo cái vòng lặp vô tận kia.

Kết:

Dải băng mobius là một biểu tượng đầy lý thú và mang tính triết lý sâu sắc nên nếu bạn có trí tưởng tượng phong phú và chịu khó “động não” sẽ phát hiện khá nhiều điều thú vị. Đại diện cho sự thay đổi liên tục trong tâm trí ta và trong cuộc sống, một dãy “xoắn” đem lại niềm tin cho chúng ta về hiện diện lẽ phải và giá trị sống tinh thần mà ta buộc phải chấp nhận nhiều thứ. Ở đây tôi đã cố gắng dùng ngôn từ đơn giản, dễ hiểu, gần gũi cho tất cả mọi người có thể dễ dàng hình dung những quy luật sống mà các bạn nên nắm rõ để có cái nhìn sâu sắc và toàn diện hơn.

Tác Giả: Thao Tran

Sinh viên Đại học Tài Nguyên Và Môi Trường TPHCM

Kết bạn và theo dõi facebook của tác giả tại link: https://www.facebook.com/profile.php?id=100008449053008

--------------------------------

Bạn đam mê viết lách, nhận giải thưởng (1 triệu VNĐ / tháng, sách, chứng nhận Social Impact Awards) và muốn được tạo thương hiệu cá nhân tới hàng triệu người trong cộng đồng của YBOX.VN? Xem chi tiết tại link:http://bit.ly/TrietHocTuoiTre-Info

(*) Bản quyền bài viết thuộc về Cuộc thi Triết học Tuổi trẻ do Ybox đồng sáng lập và tổ chức. Khi chia sẻ, cần phải trích dẫn nguồn đầy đủ tên tác giả và nguồn là "Tên tác giả - Nguồn: Triết Học Tuổi Trẻ". Các bài viết trích nguồn không đầy đủ cú pháp đều không được chấp nhận và phải gỡ bỏ.

----------------------------

Hợp Tác Cùng YBOX.VN Truyền Thông Miễn Phí - Trả Phí Theo Yêu Cầu tại http://bit.ly/YBOX-Partnership

18,907 lượt xem, 17,561 người xem - 17561 điểm

Thích 0Không thích 0Chia sẻ Lưu bài Có thể bạn thích