Đại Số 8/Chương IV/§4. Bất Phương Trình Bậc Nhất Một ẩn - VLOS
Có thể bạn quan tâm



Với 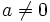 , nếu , nếu 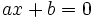 thì thì 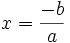 . Thế còn . Thế còn 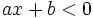 thì thì 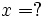 |
Mục lục
- 1 Lí thuyết
- 1.1 Định nghĩa
- 1.2 Hai quy tắc biến đổi bất phương trình
- 1.2.1 Quy tắc chuyển vế
- 1.2.2 Quy tắc nhân với một số
- 1.3 Giải bất phương trình bậc nhất một ẩn
- 1.4 Giải bất phương trình đưa được về dạng bậc nhất một ẩn
- 2 BÀI TẬP
- 3 Xem thêm
- 4 Tài liệu tham khảo
Lí thuyết[sửa]
Định nghĩa[sửa]
Bất phương trình dạng: 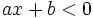 (hoặc |
| Hoạt động 1 | Trong các bất phương trình sau, hãy cho biết bất phương trình nào là bất phương trình bậc nhất một ẩn: a) 2x - 3 < 0; b) 0.x + 5 > 0; c) 5x - 15 ≥ 0; d) x2 > 0. |
Hai quy tắc biến đổi bất phương trình[sửa]
Quy tắc chuyển vế[sửa]
Từ liên hệ giữa thứ tự và phép cộng, ta có quy tắc sau (gọi là quy tắc chuyển vế) để biến đổi tương đương bất phương trình:
| Khi chuyển vế một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó. |
| VÍ DỤ 1 | Giải các bất phương trình sau: a) x - 5 < 18; b) 3x > 2x + 5 (có biểu diễn tập nghiệm trên trục số). |
| Lời giải | a) Ta có: x - 5 < 18  x < 18 + 5 (Chuyển vế -5 và đổi dấu thành 5) x < 18 + 5 (Chuyển vế -5 và đổi dấu thành 5)  x < 23. x < 23. Vậy tập nghiệm của bất phương trình là b) Ta có: 3x > 2x + 5 3x - 2x > 5 (Chuyển vế 2x và đổi dấu thành -2x) 3x - 2x > 5 (Chuyển vế 2x và đổi dấu thành -2x)  x > 5. x > 5. Vậy tập nghiệm của bất phương trình là Tập nghiệm này được biểu diễn trên trục số như sau: |
| Hoạt động 2 | Giải các bất phương trình sau: a) x + 12 > 21; b) -2x > -3x - 5. |
Quy tắc nhân với một số[sửa]
Từ liên hệ giữa thứ tự và phép nhân, ta có quy tắc sau (gọi là quy tắc nhân) để biến đổi tương đương bất phương trình:
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
|
| VÍ DỤ 2 | Giải các bất phương trình sau: a) 0,5x < 3; b) |
| Lời giải | a) Ta có: 0,5x < 3  0,5x.2 < 3.2 (Nhân cả hai vế với 2) 0,5x.2 < 3.2 (Nhân cả hai vế với 2)  x < 6. x < 6. Vậy tập nghiệm của bất phương trình là b) Ta có: 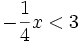 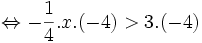 (Nhân cả hai vế với -4 và đổi chiều) (Nhân cả hai vế với -4 và đổi chiều)  x > -12. x > -12. Vậy tập nghiệm của bất phương trình là Tập nghiệm này được biểu diễn trên trục số như sau: |
| Hoạt động 3 | Giải các bất phương trình sau (dùng quy tắc nhân): a) 2x < 24; b) -3x < 27. |
| Hoạt động 4 | Giải thích sự tương đương: a) x + 3 < 7 |
Giải bất phương trình bậc nhất một ẩn[sửa]
| VÍ DỤ 3 | Giải bất phương trình 2x - 3 < 0 và biểu diễn tập nghiệm trên trục số. |
| Lời giải | Ta có: 2x - 3 < 0  2x < 3 (Chuyển -3 sang vế phải và đổi dấu) 2x < 3 (Chuyển -3 sang vế phải và đổi dấu)  2x:2 < 3:2 (Chia hai vế cho 2) 2x:2 < 3:2 (Chia hai vế cho 2)  x < 1,5. x < 1,5. Vậy tập nghiệm của bất phương trình là |
| Hoạt động 5 | Giải bất phương trình -4x - 8 < 0 và biểu diễn tập nghiệm trên trục số. Hướng dẫn: Làm tương tự ví dụ 3, nhưng lưu ý khi nhân hai vế với số âm. |
- Không ghi câu giải thích;
- Khi có kết quả x < 1,5 (ở ví dụ 3) thì coi là giải xong và viết đơn giản:
| VÍ DỤ 4 | Giải bất phương trình -4x + 12 < 0. |
| Lời giải | Ta có: -4x + 12 < 0  12 < 4x 12 < 4x  12:4 < 4x : 4 12:4 < 4x : 4  3 < x. 3 < x. Vậy nghiệm của bất phương trình là x > 3. |
Giải bất phương trình đưa được về dạng bậc nhất một ẩn[sửa]
| VÍ DỤ 5 | Giải bất phương trình 3x + 5 < 5x - 7. |
| Lời giải | Ta có: 3x + 5 < 5x - 7  3x - 5x < -5 - 7 3x - 5x < -5 - 7  -2x < -12 -2x < -12  -2x : (-2) > -12 : (-2) -2x : (-2) > -12 : (-2)  x > 6. x > 6. Vậy nghiệm của bất phương trình là x > 6. |
| Hoạt động 6 | Giải bất phương trình -0,2x - 0,2 > 0,4x - 2. |
BÀI TẬP[sửa]
8. Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (Kể ba bất phương trình có cùng tập nghiệm).
a)
b)
9. Kiểm tra xem giá trị x = -2 có là nghiệm của bất phương trình sau không:
a) 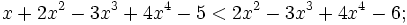
b) 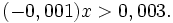
Xem thêm[sửa]
- Đại số 8/Chương IV/§3. Bất phương trình một ẩn
Tài liệu tham khảo[sửa]
- Sách in: Toán 8, tập 2, Nhà xuất bản Giáo dục, 2004, trang 43.
<<< Đại số 8
Bài này là bài sơ thảo. Bạn có thể hoàn thiện bằng cách viết bổ sung vào đây. (Xin xem phần trợ giúp để biết thêm về cách sửa đổi bài.)Liên kết đến đây
- Đại số 10/Chương IV/§2. Bất phương trình và hệ bất phương trình một ẩn
Từ khóa » Khi Nào đổi Chiều Dấu Lớn Bé
-
Lí Thuyết Bất Phương Trình Bậc Nhất Một ẩn Và Cách Giải Hay
-
Quy Tắc Biến đổi Phương Trình Và Bất Phương Trình Bậc Nhất Một ẩn
-
Lý Thuyết Bất Phương Trình Bậc Nhất Một ẩn | SGK Toán Lớp 8
-
Bất Phương Trình Bậc Nhất Một ẩn
-
HAI QUY TẮC BIẾN ĐỔI BẤT PHƯƠNG TRÌNH - Tài Liệu Text - 123doc
-
Nêu Quy Tắc Biến đổi Phương Trình,bất Phương Trình
-
Lý Thuyết Bất Phương Trình Bậc Nhất Một ẩn Toán 8
-
Cách đổi Dấu Trong Tính Toán? | Cộng đồng Học Sinh Việt Nam
-
Lưu ý Khi Giải Bất Phương Trình? - TopLoigiai
-
[CHUẨN NHẤT] Quy Tắc đổi Dấu Lớp 8 - Toploigiai
-
Phát Biểu Quy Tắc Chuyển Vế để Biến đổi Bất Phương Trình - Khóa Học
-
Khi Nào đổi Dấu Phương Trình đổi Dấu Lớn Bé á Câu Hỏi 1862789
-
Bất Phương Trình Bậc Nhất Một ẩn - Toán Lớp 8 [Online Math - ]
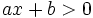 ,
, 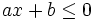 ,
, 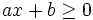 )
)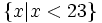 .
.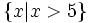 .
.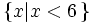 .
.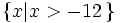 .
.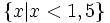 và được biểu diễn trên trục số như sau:
và được biểu diễn trên trục số như sau: