Đạo Hàm Riêng – Wikipedia Tiếng Việt

Một phần của loạt bài về
Vi tích phân
Định lý cơ bản Quy tắc tích phân Leibniz Giới hạn của hàm số Tính liên tục Định lý giá trị trung bình Định lý Rolle
Vi phân Định nghĩa Đạo hàm (Tổng quát) Vi phân vô cùng bé hàm số toàn phần Khái niệm Ký hiệu vi phân Đạo hàm bậc hai Vi phân ẩn Định lý Taylor Quy tắc và đẳng thức Cộng Nhân Dây chuyền Lũy thừa Chia Quy tắc l'Hôpital Hàm ngược Leibniz tổng quát Công thức Faà di Bruno
Tích phân Danh sách tích phân Biến đổi tích phân Định nghĩa Nguyên hàm Tích phân (suy rộng) Tích phân Riemann Tích phân Lebesgue Tích phân theo chu tuyến Tích phân của hàm ngược Kỹ thuật Từng phần Đĩa Vỏ Thế (lượng giác, Weierstrass, Euler) Công thức Euler Đổi trật tự Công thức truy hồi Lấy đạo hàm dưới dấu tích phân
Chuỗi Hình học (số học-hình học) Điều hòa Đan dấu Lũy thừa Nhị thức Taylor Tiêu chuẩn hội tụ Số hạng d'Alembert Cauchy Tích phân So sánh So sánh giới hạn Chuỗi đan dấu Cô đọng Cauchy Dirichlet Abel
Vectơ Gradien Div Rot Laplace Đạo hàm có hướng Đẳng thức Định lý Gauss Gradient Green Kelvin–Stokes Stokes
Nhiều biến Chủ đề Ma trận Tenxơ Đạo hàm ngoài Hình học Định nghĩa Đạo hàm riêng Tích phân bội Tích phân đường Tích phân mặt Tích phân thể tích Ma trận Jacobi Ma trận Hesse
Chuyên ngành Malliavin Ngẫu nhiên Phép tính biến phân
Thuật ngữ Thuật ngữ giải tích
x t s

Trong toán học, đạo hàm riêng của một hàm số đa biến là đạo hàm theo một biến, các biến khác được xem như là hằng số(khác với đạo hàm toàn phần, khi tất cả các biến đều biến thiên). Đạo hàm riêng được sử dụng trong giải tích vector và hình học vi phân.

Đạo hàm riêng của f đối với biến x được ký hiệu khác nhau bởi

f x ′ ,   f x ,   f , x ,   ∂ x f ,  hoặc  ∂ f ∂ x {\displaystyle f_{x}^{\prime },\ f_{x},\ f_{,x},\ \partial _{x}f,{\text{ hoặc }}{\frac {\partial f}{\partial x}}}

Ký hiệu của đạo hàm riêng là ∂. Ký hiệu này được giới thiệu bởi Adrien-Marie Legendre và được chấp nhận rộng rãi sau khi nó được giới thiệu lại bởi Carl Gustav Jacob Jacobi.[1]

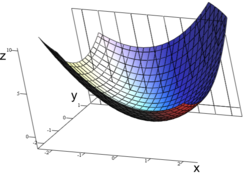Đồ thị của hàm số z = x2 + xy + y2. Đạo hàm riêng tại điểm (1, 1, 3) với y là hằng số tương ứng với đường tiếp tuyến song song với mặt phẳng xz.Mặt cắt của đồ thị trên tại y= 1

Định nghĩa

[sửa | sửa mã nguồn]

Ví dụ sau sẽ giúp giải thích định nghĩa của đạo hàm riêng theo biến y.Giả sử một hàm theo hai biến x,y được xem như là một họ các hàm theo y được đánh số theo x

f ( x , y ) = f x ( y ) = x 2 + x y + y 2 . {\displaystyle f(x,y)=f_{x}(y)=\,\!x^{2}+xy+y^{2}.\,}

Nói một cách khác, mỗi giá trị của x định nghĩa một hàm số, ký hiệu là fx, mà nó là hàm số một biến. Nghĩa là

f x ( y ) = x 2 + x y + y 2 . {\displaystyle f_{x}(y)=x^{2}+xy+y^{2}.\,}

Một khi giá trị của x được chọn, ví dụ là a, thì f(x,y) xác định một hàm số fa

f a ( y ) = a 2 + a y + y 2 . {\displaystyle f_{a}(y)=a^{2}+ay+y^{2}.\,}

Trong công thức này, a là hằng số, không phải là biến số, do đó fa là một hàm số một biến và do vậy ta có thể sử dụng định nghĩa đạo hàm cho hàm một biến:

f a ′ ( y ) = a + 2 y . {\displaystyle f_{a}'(y)=a+2y.\,}

Quy trình trên có thể được áp dụng cho bất cứ lựa chọn nào của a. Khi đem gộp lại tất cả những đạo hàm đó ta có được sự biến thiên của hàm số f theo hướng của y:

∂ f ∂ y ( x , y ) = x + 2 y . {\displaystyle {\frac {\partial f}{\partial y}}(x,y)=x+2y.\,}

Đây là đạo hàm riêng của f theo biến số y. Ổ đây ∂ được gọi là ký hiệu đạo hàm riêng.

Một cách tổng quát, đạo hàm riêng của một hàm số f(x1,...,xn) theo hướng xi tại điểm (a1,...,an) được định nghĩa là:

∂ f ∂ x i ( a 1 , … , a n ) = lim h → 0 f ( a 1 , … , a i + h , … , a n ) − f ( a 1 , … , a i , … , a n ) h . {\displaystyle {\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{i},\dots ,a_{n})}{h}}.}

Trong tỷ số bên trên, tất cả các biến ngoại trừ xi được giữ cố định. Do vậy ta chỉ có hàm số theo một biến f a 1 , … , a i − 1 , a i + 1 , … , a n ( x i ) = f ( a 1 , … , a i − 1 , x i , a i + 1 , … , a n ) {\displaystyle f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})} , và do định nghĩa,,

d f a 1 , … , a i − 1 , a i + 1 , … , a n d x i ( x i ) = ∂ f ∂ x i ( a 1 , … , a n ) . {\displaystyle {\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(x_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).}

Một ví dụ quan trọng của đạo hàm riêng: Cho một hàm số f(x1,...xn) đinh nghĩa trên một miền của Rn (ví dụ, trên R2 hay là R3). Trong trường hợp này f có các đạo hàm riêng ∂f/∂xj đối với mỗi biến xj. Tại điểm a, những đạo hàm riêng này định ra vector

∇ f ( a ) = ( ∂ f ∂ x 1 ( a ) , … , ∂ f ∂ x n ( a ) ) . {\displaystyle \nabla f(a)=\left({\frac {\partial f}{\partial x_{1}}}(a),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a)\right).}

Vector này được gọi là gradient của f tại a. Nếu f khả vi tại mọi điểm trong một miền nào đó, thì gradient là hàm số có trị là vectơ ∇f đưa điểm a đến vectơ ∇f(a). Do đó gradient là một trường vectơ.

Ghi chú

[sửa | sửa mã nguồn]

1. ^ Jeff Miller (ngày 14 tháng 6 năm 2009). “Earliest Uses of Symbols of Calculus”. Earliest Uses of Various Mathematical Symbols. Truy cập ngày 20 tháng 2 năm 2010.

Liên kết ngoài

[sửa | sửa mã nguồn]

• Partial Derivatives trên MathWorld