Định Lí Pi-ta-go - Chuyên đề Toán Học Lớp 7

• • 
    • 

      Mầm non

    • 

      Lớp 1

    • 

      Lớp 2

    • 

      Lớp 3

    • 

      Lớp 4

    • 

      Lớp 5

    • 

      Lớp 6

    • 

      Lớp 7

    • 

      Lớp 8

    • 

      Lớp 9

    • 

      Lớp 10

    • 

      Lớp 11

    • 

      Lớp 12

    • 

      Thi vào lớp 6

    • 

      Thi vào lớp 10

    • 

      Thi Tốt Nghiệp THPT

    • 

      Đánh Giá Năng Lực

    • 

      Khóa Học Trực Tuyến

    • 

      Hỏi bài

    • 

      Trắc nghiệm Online

    • 

      Tiếng Anh

    • 

      Thư viện Học liệu

    • 

      Bài tập Cuối tuần

    • 

      Bài tập Hàng ngày

    • 

      Thư viện Đề thi

    • 

      Giáo án - Bài giảng

    • 

      Tất cả danh mục

  • Mầm non
  • Lớp 1
  • Lớp 2
  • Lớp 3
  • Lớp 4
  • Lớp 5
  • Lớp 6
  • Lớp 7
  • Lớp 8
  • Lớp 9
  • Lớp 10
  • Lớp 11
  • Lớp 12
  • Thi Chuyển Cấp

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày

• Hôm nay +3
• Ngày 2 +3
• Ngày 3 +3
• Ngày 4 +3
• Ngày 5 +3
• Ngày 6 +3
• Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 8 Bài tập Toán 8 Bài tập Định lí Pythagore lớp 8 Chuyên đề Toán học lớp 8 Bài trước Tải về Bài sau Lớp: Lớp 7 Môn: Toán Loại File: Word Phân loại: Tài liệu Tính phí

Chuyên đề Toán học lớp 8: Định lí Pythagore được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.

Chuyên đề: Định lí Pythagore

• A. Lý thuyết
  • 1. Định lý Pythagore
  • 2. Định lý Pythagore đảo
• B. Bài tập trắc nghiệm về định lí Pythagore
• C. Bài tập tự luận 
  • 1. Dạng 1. Tính độ dài cạnh của tam giác vuông
  • 2. Dạng 2: Nhận biết tam giác vuông 
  • 3. Dạng 3. Dùng định lý Pythagore giải quyết một số bài toán thực tế liên quan.
• D. Bài tập tự luyện

A. Lý thuyết

1. Định lý Pythagore

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Δ ABC vuông tại A ⇒ BC2 = AB2 + AC2

2. Định lý Pythagore đảo

Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

Δ ABC có BC2 = AB2 + AC2 thì \(\widehat{BAC}\) = 90o

B. Bài tập trắc nghiệm về định lí Pythagore

Bài 1: Cho tam giác ABC vuông tại B. Khi đó

A. AB2 + BC2 = AC2 B. AB2 – BC2 = AC2

C. AB2 + AC2 = BC2 D. AB2 = AC2 + BC2

Giải thích: Ta có tam giác ABC vuông tại B, theo định lí Pythagore ta có: AB2 + BC2 = AC2

Chọn đáp án A.

Bài 2: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB = AC = 2 dm

A. BC = 4 dm B. BC = √6 dm

C. BC = 8 dm D. BC = √8 dm

Giải thích: Áp dụng định lí Pythagore ta có: BC2 = AB2 + AC2

Khi đó ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{4+4}=\sqrt{8}\) (dm)

Chọn đáp án D.

Bài 3: Một tam giác vuông có cạnh huyền bằng 26 cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?

A. 10 cm, 22 cm B. 10 cm, 24 cm

C. 12 cm, 24 cm D. 15 cm, 24 cm

Giải thích: Gọi độ dài các cạnh góc vuông lần lượt là x, y (x, y > 0)

Áp dụng định lí Pythagore ta có:

x2 + y2 = 262 ⇔ x2 + y2 = 676

Theo bài ra ta có: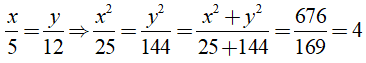

Khi đó ta có: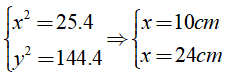

Chọn đáp án B.

Bài 4: Cho tam giác ABC vuông tại A có AC = 20 cm. Kẻ AH vuông góc với BC. Biết BH = 9 cm, HC = 16 cm. Tính độ dài cạnh AB, AH?

A. AH = 12 cm, AB = 15 cm

B. AH = 10 cm, AB = 15 cm

C. AH = 15 cm, AB = 12 cm

D. AH = 12 cm, AB = 13 cm

Giải thích:

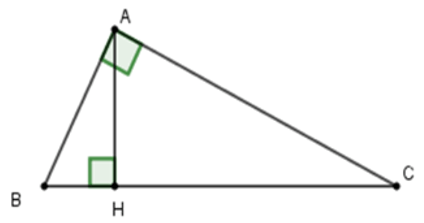
Ta có: BC = HB + HC = 9 + 16 = 25 (cm)

Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:

BC2 = AB2 + AC2

⇒ AB2 = BC2 – AC2

= 252 – 202 = 225

⇒ AB = 15 cm

Xét tam giác ABH vuông tại H, theo định lí Pythagore ta có:

HB2 + HA2 = AB2

⇒ AH2 = AB2 – HB2

= 152 – 92 = 144

⇒ AH = 12 cm

Vậy AH = 12 cm, AB = 15 cm

Chọn đáp án A.

Bài 5: Cho hình vẽ. Tính x

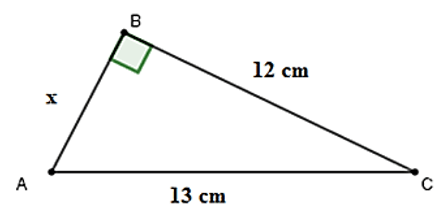
A. x = 10 cm

B. x = 11 cm

C. x = 8 cm

D. x = 5 cm

Giải thích: Xét tam giác ABC vuông tại B ta có:

⇒ x2 + 122 = 132 ⇒ x2 = 132 – 122 = 25

Khi đó: x = 5 cm

Chọn đáp án D.

C. Bài tập tự luận 

1. Dạng 1. Tính độ dài cạnh của tam giác vuông

Ví dụ 1: Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 8 cm.

a) Tính độ dài cạnh BC.

b) Kẻ AH vuông góc với BC tại H. Biết AH = 4,8 cm. Tính BH, CH.

Lời giải:

a) Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có: 

BC2 = AB2 + AC2 = 62 + 82 = 100

⇒ BC = 10 cm

b) Xét tam giác ABH vuông tại H, áp dụng định lí Pythagore, ta có:

AB2 = AH2 + HB2  

⇒ BH2 = AB2 - AH2 = 62 - 4,82 = 12,96

⇒ BH = 3,6 cm

Do đó CH = BC - BH = 10 - 3,6 = 6,4 cm.

2. Dạng 2: Nhận biết tam giác vuông 

Ví dụ 2: Kiểm tra xem tam giác nào là tam giác vuông trong các tam giác có độ dài sau:

a) 4 cm, 7 cm, 6 cm;

b) 5 cm, 13 cm, 12 cm.

Lời giải:

a) Ta có 42 + 62 = 52 ≠ 49 = 72 nên tam giác này không phải là tam giác vuông.

b) Ta có: 52 + 122 = 169 = 132 nên tam giác này là tam giác vuông.

Ví dụ 3: Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 8 cm. D là một điểm sao cho BD = 16 cm, CD = 24 cm. Chứng minh tam giác BCD không thể là tam giác vuông.

Lời giải:

Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:

BC2 = AB2 + AC2 = 62 + 82 = 100

⇒ BC = 10 cm

Ta có: BC2 + BD2 = 356 ≠ 576 = 242 nên tam giác BCD không thể là tam giác vuông.

3. Dạng 3. Dùng định lý Pythagore giải quyết một số bài toán thực tế liên quan.

Ví dụ 4: Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170 m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80 m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2 m.

Lời giải:

Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:

BC2 = AB2 + AC2

⇒ AB2 = BC2 - AC2 = 1702 - 802 = 22 500

⇒ AB = 150 m

Vậy độ cao của con diều so với mặt đất là: 150 + 2 = 152 cm.

D. Bài tập tự luyện

Tải file để xem đáp án chi tiết!

Tải về Chọn file muốn tải về:

Bài tập Định lí Pythagore lớp 8

393 KB

• Chia sẻ bởi: Nguyễn Nam Hoài

26 23.023 Bài viết đã được lưu Bài trước Mục lục Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin 1 Bình luận Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi

• linh nguyễn

  good

  Thích · Phản hồi · 1 · 16/02/22

Tìm bài trong mục này

• SỐ HỮU TỈ

  • Tập hợp các số hữu tỉ
  • Cộng trừ số hữu tỉ
  • Nhân, chia số hữu tỉ
  • Lũy thừa với số mũ tự nhiên của một số hữu tỉ
  • Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

• SỐ THỰC

  • Số thập phân hữu hạn - Số thập phân vô hạn tuần hoàn
  • Số vô tỉ. Căn bậc hai số học
  • Tập hợp các số thực

• GÓC VÀ ĐƯỜNG THẲNG SONG SONG

  • Góc ở vị trí đặc biệt
  • Tia phân giác của một góc
  • Hai đường thẳng song song
  • Tiên đề Euclid. Tính chất của hai đường thẳng song song
  • Định lý

• TAM GIÁC BẰNG NHAU

  • Tổng ba góc của một tam giác
  • Hai tam giác bằng nhau
  • Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
  • Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
  • Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
  • Các trường hợp bằng nhau của tam giác vuông
  • Tam giác cân. Đường trung trực của đoạn thẳng

• TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LÊ

  • Tỉ lệ thức
  • Tính chất của dãy tỉ số bằng nhau
  • Đại lượng tỉ tệ thuận
  • Đại lượng tỉ lệ nghịch

• BIỂU THỨC ĐẠI SỐ VÀ ĐA THỨC MỘT BIẾN

  • Khái niệm về biểu thức đại số
  • Giá trị của một biểu thức đại số
  • Đơn thức
  • Đơn thức đồng dạng
  • Đa thức
  • Cộng, trừ đa thức
  • Đa thức một biến
  • Cộng, trừ đa thức một biến
  • Nghiệm của đa thức một biến

• QUAN HỆ GIỮA CÁC YÊU TỐ TRONG TAM GIÁC

  • Quan hệ giữa góc và cạnh đối diện trong một tam giác
  • Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
  • Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác
  • Tính chất ba đường trung tuyến của tam giác
  • Tính chất ba đường phân giác của tam giác
  • Tính chất đường trung trực của một đoạn thẳng
  • Tính chất ba đường trung trực của tam giác
  • Tính chất ba đường cao của tam giác

• MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN

  • Hình hộp chữ nhật
  • Hình lập phương
  • Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

• XÁC SUẤT

• Lớp 8

• Bài tập Toán 8

• Đề thi giữa kì 1 lớp 8

• Đề thi học kì 1 lớp 8

• Đề thi giữa kì 2 lớp 8

• Đề thi học kì 2 lớp 8

• Đề kiểm tra 15 phút lớp 8

• Thi học sinh giỏi lớp 8

• Toán 8

• Toán 8 Kết nối tri thức

• Toán 8 Chân trời sáng tạo

• Toán 8 Cánh diều

• Giải Bài Tập Toán 8

• Lý thuyết Toán 8

• Soạn Toán 8 VNEN

Tham khảo thêm

• Bài tập Định lí Pythagore lớp 8

• Giải bài tập SBT Toán 7 bài 7: Định lí Pi-ta-go

• Bài tập Phân thức đại số Toán 8

• Bài tập Định lý Thales trong tam giác lớp 8

• Bài tập phân tích đa thức thành nhân tử lớp 8

• Bài tập nâng cao Toán lớp 8: Phân tích đa thức thành nhân tử

• Bài tập Tính chất đường phân giác của tam giác lớp 8

• Bài tập Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8

• Bài tập nâng cao Toán lớp 8: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

• Bài tập Đường trung bình của tam giác lớp 8

Bài tập Toán 8

• Bài tập Phân thức đại số Toán 8

• Bài tập Định lý Thales trong tam giác lớp 8

• Bài tập Định lí Pythagore lớp 8

• Bài tập Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8

• Bài tập Đường trung bình của tam giác lớp 8

• Bài tập Tính chất đường phân giác của tam giác lớp 8

Xem thêm

Gợi ý cho bạn

• Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1

• Được 18-20 điểm khối A1 nên đăng ký trường nào?

• Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao

• TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4

Xem thêm

Bài tập Định lí Pythagore lớp 8

Bài tập Định lí Pythagore lớp 8

Chỉ mua tài liệu trên 25.000đ Ưu đãi kèm thêm

Mua gói VnDoc Pro chỉ với giá

79.000đ 59.000đ

• 30 lượt tải tài liệu thường
• 10.000+ bài luyện Trắc nghiệm trực tuyến
• Không quảng cáo

Mua tài liệu này và Gói Thành viên 84.000đ ×

Thông tin thanh toán nhanh

Tên tài liệu:

Bài tập Định lí Pythagore lớp 8

25.000đ

Số điện thoại/email

Vui lòng nhập số điện thoại hoặc email hợp lệ.

Tải nhanh tài liệu này 25.000đ Hỗ trợ Zalo × ← Thanh toán 25.000đ để tải tài liệu

• Tên tài khoản:CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META
• Số tài khoản:1038633514Copy
• Ngân hàng:Vietcombank
• Số tiền:25.000đ
• Nội dung bắt buộc*: Copy

Vui lòng giữ đúng nội dung KH khi chuyển khoản và giữ nguyên cửa sổ này để tải tài liệu tự động.

Hỗ trợ Zalo