Định Nghĩa, Tính Chất, Dấu Hiệu Nhận Biết Các Hình Học Phẳng Lớp 8
Có thể bạn quan tâm
-
-

-
Mầm non
-
Lớp 1
-
Lớp 2
-
Lớp 3
-
Lớp 4
-
Lớp 5
-
Lớp 6
-
Lớp 7
-
Lớp 8
-
Lớp 9
-
Lớp 10
-
Lớp 11
-
Lớp 12
-
Thi vào lớp 6
-
Thi vào lớp 10
-
Thi Tốt Nghiệp THPT
-
Đánh Giá Năng Lực
-
Khóa Học Trực Tuyến
-
Hỏi bài
-
Trắc nghiệm Online
-
Tiếng Anh
-
Thư viện Học liệu
-
Bài tập Cuối tuần
-
Bài tập Hàng ngày
-
Thư viện Đề thi
-
Giáo án - Bài giảng
-
Tất cả danh mục
-
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp
-
- Hôm nay +3
- Ngày 2 +3
- Ngày 3 +3
- Ngày 4 +3
- Ngày 5 +3
- Ngày 6 +3
- Ngày 7 +5
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloĐịnh nghĩa, tính chất, dấu hiệu nhận biết các hình học phẳng lớp 8
- I/ Hình Thang cân
- 1/ Định nghĩa hình thang cân
- 2/ Tính chất hình thang cân
- 3/ Dấu hiệu nhận biết hình thang cân
- 4. Bài tập minh họa
- II/ Hình bình hành
- 1/ Định nghĩa hình bình hành
- 2/ Tính chất hình bình hành
- 3/ Dấu hiệu nhận biết hình bình hành
- III/ Hình chữ nhật
- 1/ Định nghĩa hình chữ nhật
- 2/ Tính chất hình chữ nhật
- 3/ Dấu hiệu nhận biết hình chữ nhật
- IV/ Hình thoi
- 1/ Định nghĩa hình thoi
- 2/ Tính chất hình thoi
- 3/ Dấu hiệu nhận biết hình thoi
- 4/ Bài tập minh họa
- V/ Hình vuông
- 1/ Định nghĩa hình vuông
- 2/ Tính chất hình vuông
- 3/ Dấu hiệu nhận biết hình vuông
- VI/ Bài tập vận dụng
Định nghĩa, tính chất, dấu hiệu nhận biết các hình học phẳng giúp các em nắm được định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân, hình bình hành, hình thoi, hình vuông, từ đó áp dụng tốt vào giải các bài tập Toán 8. Dưới đây là nội dung chi tiết các em tham khảo nhé.
- Bài tập phân tích đa thức thành nhân tử
- Toán lớp 8: 7 Hằng Đẳng Thức Đáng Nhớ Và Hệ Quả
I/ Hình Thang cân
1/ Định nghĩa hình thang cân
– Hình thang cân là hình thang có hai góc kề 1 đáy bằng nhau
2/ Tính chất hình thang cân
– Hình thang cân có:
• Hai góc kề một đáy bằng nhau
• Hai cạnh bên bằng nhau
• Hai đường chéo bằng nhau
3/ Dấu hiệu nhận biết hình thang cân
– Hình thang có:
• hai góc kề bằng nhau là hình thang cân
• hai đường chéo bằng nhau là hình thang cân
4. Bài tập minh họa
Bài tập 1: Chứng minh hình thang cân:
Ví dụ 1: Hình thang ABCD (AB // CD) có góc ACD = góc BDC. Chứng minh rằng ABCD là hình thang cân.
Lời giải:
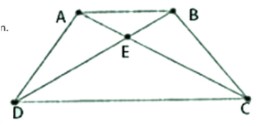
Gọi E là giao điểm của AC và BD.
Do góc ACD = góc BCD nên tam giác ECD có góc C1 = góc D1, nên là tam giác cân.
Từ đó suy ra EC = ED. (1)
Tương tự do góc ACD = góc BCD và AB // CD nên tam giác EAB cân tại E, suy ra EA = EB. (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED ⇒ AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên hình thang ABCD là hình thang cân (điều phải chứng minh).
Ví dụ 2: Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng mình EA = EB, EC = ED.
Lời giải:

Do ABCD là hình thang cân (giả thiết) nên AD = BC, AC = BD (tính chất hình thang cân)
Xét tam giác ADC và tam giác BCD có:
AD = BC (chứng minh trên)
AC = BD (chứng mình trên)
DC chung
⇒ Tam giác ADC = tam giác BCD (cạnh – cạnh – cạnh)
Suy ra góc ACD = góc BDC (2 góc tương ứng)
Do đó tam giác EDC cân tại E (dấu hiệu nhận biết tam giác cân)
⇒ EC = ED (tính chất tam giac cân)
Lại có: AC = BD (chứng minh trên), EC = ED (chứng minh trên)
⇒ AC – CE = BD – ED
⇒ EA = EB
Vậy EA = EB và EC = ED (điều phải chứng minh).
II/ Hình bình hành
1/ Định nghĩa hình bình hành
– Là tứ giác có các cạnh đối song song
2/ Tính chất hình bình hành
– Hình bình hành có:
• Các cạnh đối bằng nhau
• Các góc đối bằng nhau
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường
3/ Dấu hiệu nhận biết hình bình hành
– Tứ giác có:
• Các cạnh đối song song là hình bình hành
• Các cạnh đối bằng nhau là hình bình hành
• Hai cạnh đối song song và bằng nhau là hình bình hành
• Các góc đối bằng nhau là hình bình hành
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
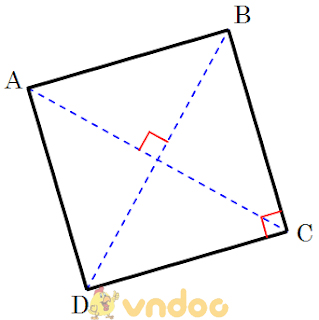
III/ Hình chữ nhật
1/ Định nghĩa hình chữ nhật
– Là tứ giác có 4 góc vuông
2/ Tính chất hình chữ nhật
– Hình chữ nhật có:
• Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
• tất cả các tính chất của hình thang cân và hình thoi.
3/ Dấu hiệu nhận biết hình chữ nhật
– Tứ giác có 3 góc vuông là hình chữ nhật
– Hình thang cân có 1 góc vuông là hình chữ nhật
– Hình bình hành có 1 góc vuông là hình chữ nhật
– Hình bình hành có 2 đường chéo bằng nhau là hình chữ nhật
IV/ Hình thoi
1/ Định nghĩa hình thoi
– Hình thoi là tứ giác có 4 cạnh bằng nhau
2/ Tính chất hình thoi
– Trong hình thoi có:
• Hai đường chéo vuông góc với nhau
• Hai đường chéo là các đường phân giác của các góc của hình thoi và cắt nhau tại trung điểm của mỗi đường
• Tất cả các tính chất của hình bình hành
3/ Dấu hiệu nhận biết hình thoi
– Tứ giác có 4 cạnh bằng nhau là hình thoi
– Hình bình hành có hai cạnh kề bằng nhau là hình thoi
– Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
– Hình bình hành có 1 đường chéo là đường phân giác của một góc là hình thoi
4/ Bài tập minh họa
Ví dụ 1: Cho hình thoi ABCD, độ dài mỗi cạnh là 13 cm. Gọi O là giao điểm của hai đường chéo. Vẽ OH vuông góc AD. Biết OH = 6 cm, tính tỉ số của hai đường chéo BD và AC.
Lời giải:
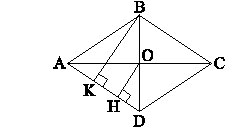
Vẽ BK vuông góc AD.
Xét DBKD có OH // BK (vì cùng vuông góc với AD) và OB = OD nên KH = HD.
Vậy OH là đường trung bình của DBKD.
Suy ra do đó BK = 12 cm.
Xét DABK vuông tại K có:
AK2 = AB2 – BK2 = 132 – 122 = 25
⇒ AK = 5 cm do đó KD = 8 cm.
Xét tam giác BKD vuông tại K có:
BD2 = BK2 + KD2 = 122 + 82 = 208.
Xét tam giác AOH vuông tại H có:
OA2 = OH2 + AH2 = 62 + 92 = 117.
Ví dụ 2: Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là hình chiếu của G trên AB và AC. Chứng minh rằng tứ giác DNGM là hình thoi.
Lời giải:
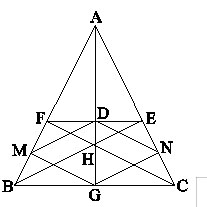
Tam giác ABE = Tam giác ACF (cạnh huyền, góc nhọn)
⇒ AE = AF và BE = CF.
Vì H là trực tâm của DABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.
Vì H là trực tâm của DABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.
Xét DEBC có GN // BE (cùng vuông góc với AC) và GB = GC nên NE = NC.
Chứng minh tương tự ta được MF = MB.
Dùng định lí đường trung bình của tam giác ta chứng minh được DM // GN và DM = GN nên tứ giác DNGM là hình bình hành.
Mặt khác, DM = DN (cùng bằng ![]() \(\frac{1}{2}\) của hai cạnh bằng nhau) nên DNGM là hình thoi.
\(\frac{1}{2}\) của hai cạnh bằng nhau) nên DNGM là hình thoi.
V/ Hình vuông
1/ Định nghĩa hình vuông
– Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
2/ Tính chất hình vuông
– Hình vuông có các tính chất của hình chữ nhật và hình thoi.
3/ Dấu hiệu nhận biết hình vuông
– Hình chữ nhật có hai cạnh kể bằng nhau là hình vuông
– Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông
– Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông
– Hình thoi có một góc vuông là hình vuông
– Hình thoi có hai đường chéo bằng nhau là hình vuông.
VI/ Bài tập vận dụng
Bài 1: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a) Tứ giác BDEC là hình gì? Vì sao?
b) Các điểm D, E ở vị trí nào thì BD = DE = EC?
Bài 2: Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo. Gọi P và Q lần lượt là trung điểm của OB, OD. Kẻ PM vuông góc với AB tại M, QN vuông góc với CD tại N. Chứng minh ba điểm M, O, N thẳng hàng và các đường thẳng AC, MN, PQ đồng quy.
Bài 3: Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh tam giác PIQ cân.
Bài 4: Cho tam giác vuông ABC tại A, M là một điểm thuộc cạnh BC. Qua M vẽ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC, AB theo thứ tự tại E và F.
a) Tứ giác AFME là hình gì?
b) Xác định vị trí điểm M trên cạnh BC để tứ giác AFME là hình vuông.
Tải về Chọn file muốn tải về:Định nghĩa, tính chất, dấu hiệu nhận biết các hình học phẳng
103,5 KB Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này! Đóng 79.000 / tháng Mua ngay Đặc quyền các gói Thành viên PRO Phổ biến nhất PRO+ Tải tài liệu Cao cấp 1 Lớp 30 lượt tải tài liệu Xem nội dung bài viết Trải nghiệm Không quảng cáo Làm bài trắc nghiệm không giới hạn Tìm hiểu thêm Mua cả năm Tiết kiệm tới 48%- Chia sẻ bởi:
 Công chúa Tuyết
Công chúa Tuyết

Có thể bạn quan tâm
Xác thực tài khoản!Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất-
 Lớp 8
Lớp 8 -
 Toán 8
Toán 8 -
 Bài tập Toán 8
Bài tập Toán 8 -
 Đề thi giữa kì 1 lớp 8
Đề thi giữa kì 1 lớp 8 -
 Đề thi học kì 1 lớp 8
Đề thi học kì 1 lớp 8 -
 Đề thi giữa kì 2 lớp 8
Đề thi giữa kì 2 lớp 8 -
 Đề thi học kì 2 lớp 8
Đề thi học kì 2 lớp 8 -
 Đề kiểm tra 15 phút lớp 8
Đề kiểm tra 15 phút lớp 8 -
 Thi học sinh giỏi lớp 8
Thi học sinh giỏi lớp 8 -
 Toán 8 Kết nối tri thức
Toán 8 Kết nối tri thức -
 Toán 8 Chân trời sáng tạo
Toán 8 Chân trời sáng tạo -
 Toán 8 Cánh diều
Toán 8 Cánh diều -
 Giải Bài Tập Toán 8
Giải Bài Tập Toán 8 -
 Lý thuyết Toán 8
Lý thuyết Toán 8 -
 Soạn Toán 8 VNEN
Soạn Toán 8 VNEN
Tham khảo thêm
-
Bài tập Đồ thị của hàm số bậc nhất y = ax + b, a ≠ 0
-
Bộ đề thi học kì 1 lớp 8 môn Ngữ Văn năm học 2021 - 2022
-
Bài tập Phương trình bậc nhất một ẩn và cách giải
-
Thuyết minh về cục tẩy
-
Bộ đề Đọc hiểu Ngữ văn 8 học kì 1
-
20 Bộ đề thi Hóa 8 học kì 2 Có đáp án
-
80 Đề thi học kì 1 lớp 8 môn Toán
-
Từ vựng tiếng Anh lớp 8 Global Success cả năm
-
Bài tập Hàm số bậc nhất y = ax + b, a ≠ 0
-
Bằng phương pháp hóa học hãy nhận biết các chất sau

Bài tập Toán 8
-
Bài tập Hàm số bậc nhất y = ax + b, a ≠ 0
-
Bài tập Phương trình bậc nhất một ẩn và cách giải
-
Bài tập Định lí Pythagore lớp 8
-
Bài tập ôn tập các trường hợp đồng dạng của tam giác
-
Bài tập Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8
-
Bài tập Đồ thị của hàm số bậc nhất y = ax + b, a ≠ 0

Gợi ý cho bạn
-
TOP 14 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4
-
Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1
-
Tổng hợp cấu trúc và từ vựng tiếng Anh lớp 3 Global Success
-
Tổng hợp từ vựng tiếng Anh lớp 9 chương trình mới
Từ khóa » Cách Tính Chất Hình Học Lớp 8
-
Công Thức Hình Học Lớp 8 đầy đủ Cả Năm, Chi Tiết Nhất
-
TỔNG HỢP KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 8 - Hocmai
-
Tổng Hợp Kiến Thức Lý Thuyết Hình Học Lớp 8 (Ngắn Gọn Nhất)
-
Định Nghĩa, Tính Chất, Dấu Hiệu Nhận Biết Các Hình Học Phẳng Lớp 8
-
Tổng Hợp Công Thức Toán Học Lớp 8 Phần Hình Học
-
CÁC CÁCH CM HÌNH HỌC 8 - Tài Liệu Text - 123doc
-
Lý Thuyết Tứ Giác Cần Ghi Nhớ - Toán Lớp 8 - Trường Quốc Học
-
✓ Công Thức Toán Lớp 8 - Gia Sư Tâm Tài Đức
-
Công Thức Hình Học Không Gian Lớp 8 - Học Toán 123
-
Tổng Hợp Lý Thuyết Chương 1 Phần Hình Học: Tứ Giác | Giải Toán 8
-
MÔN TOÁN - LỚP 8 | HÌNH HỌC: TÍNH CHẤT ĐƯỜNG PHÂN GIÁC ...
-
Cách Chứng Minh Hình Học Lớp 8 - Hàng Hiệu
-
Toán Lớp 8 Cơ Bản - Hình Học - 03. Ôn Tập Tính Góml
-
Lý Thuyết Hình Chữ Nhật | SGK Toán Lớp 8
































