Đường Chéo Hình Vuông : Công Thức, Tính Chất Và Cách Tính.
Có thể bạn quan tâm
Trong bài toán về đường chéo hình vuông có thể còn rất nhiều bạn chưa lắm rõ kiến thức về công thức tính đường chéo hình vuông, trong đó có các tính chất và chứng minh đường chéo hình vuông. Bài viết này sẽ giúp ích học sinh rất nhiều trong cách tính đường chéo hình vuông áp dụng vào các bài kiểm tra.
- Xem thêm : Công thức tính đường chéo hình hộp chữ nhật
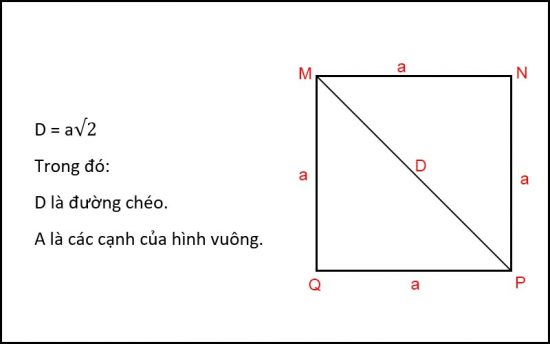
Đường chéo hình vuông là gì?
Hình vuông là tứ giác đều có 4 cạnh bằng nhau và bốn góc bằng nhau bằng. Có thể coi hình vuông là hình chữ nhật có 2 cạnh kề bằng nhau hoặc hình thoi có 2 đường chéo bằng nhau.
Đường chéo hình vuông là đường thẳng nối liền hai góc vuông đối diện nhau và chia hình vuông thành hai nửa tam giác bằng nhau.
Tính chất của đường chéo hình vuông.
Mỗi hình vuông có hai đường chéo bằng nhau, giao nhau tại trung điểm của mỗi đường và vuông góc với nhau.
+ Đường chéo sẽ chia hình vuông thành hai tam giác bằng nhau.
+ Giao điểm của hai đường chéo hình vuông là tâm của đường tròn ngoại tiếp và đường tròn nội tiếp.
+ Giao của các đường phân giác, trung tuyến, trung trực đều tùng tại một điểm.
+ Hình vuông có tất cả tính chất của hình thoi như:
- Các góc trong hình sẽ bằng nhau và đối nhau.
- Có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường và là đường phân giác của các góc trong hình.
+ Hình vuông có đầy đủ tính chất của chữ nhật:
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường và tạo thành 4 tam giác cân.
- Có 4 góc vuông bằng nhau.
- Các cạnh đối song song và bằng nhau.
Kết luận đường chéo hình vuông có 3 tính chất cần lưu ý:
- Hai đường chéo bằng nhau
- Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường
- Đường chéo chia hình vuông thành hai hình và hình đó chính là tam giác vuông cân.
Công thức tính đường chéo hình vuông.
Gọi cạnh hình vuông là a, đường chéo là b ta có:
Áp dụng định lý Pytago :
![]()
Trong đó :
- b là độ dài đường chéo hình vuông
- a là cạnh của hình vuông
Chứng minh công thức đường chéo hình vuông
Giả sử các bạn có hình vuông ABCD độ dài cạnh a, đường chéo AC chia hình vuông thành 2 tam giác vuông cân ABC và ACD.
Áp dụng định lý Pytago cho tam giác vuông cân ABC:

Bài tập ví dụ cách tính đường chéo hình vuông
Ví dụ1 : Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng bao nhiêu?
Lời giải:
Áp dụng công thức, ta có:
AC² = AB² + BC² = 3² + 3² = 18
=> đường chéo hình vuông = √18 cm
Ví dụ 2 : Cho hình vuông ABCD có cạnh a = 5cm, tính đường chéo AC, BD?

Trên đây là toàn bộ công thức tính đường chéo hình vuông và các lý thuyết tính chất, chứng minh đường chéo hình vuông mà các em cần ghi nhớ.
Ôn tập lại kiến thức :
- Tính chu vi hình vuông
- Tính diện tích hình vuông
- Tính chất và dấu hiệu nhận biết hình vuông
Từ khóa » Tính Chất Hình Vuông Và đường Chéo
-
Công Thức Tính đường Chéo Hình Vuông Chính Xác Và Bài Tập Vận Dụng
-
Đường Chéo Hình Vuông – Tính Chất Và Cách Tính - PDIAM
-
Đường Chéo Hình Vuông Có Những Tính Chất Gì - Vi Tường - HOC247
-
Công Thức Tính đường Chéo Hình Vuông
-
Công Thức Tính đường Chéo Hình Vuông, đường Chéo Hình Chữ Nhật
-
Hình Vuông Là Gì ? Tính Chất Hình Vuông ? Đường Chéo Hình Vuông ?
-
Đường Chéo Hình Vuông: Công Thức Và Bài Tập Công Thức Tính ...
-
Đường Chéo Hình Vuông,Cách Tính Và Tính Chất
-
Hình Vuông – Wikipedia Tiếng Việt
-
Cách Tính đường Chéo Hình Vuông, Hình Chữ Nhật
-
Tính Chất Hình Vuông, Dấu Hiệu Nhận Biết, định Nghĩa đầy đủ Từ A - Z
-
Công Thức Tính đường Chéo Hình Vuông - Luật Hoàng Phi
-
Định Nghĩa, Tính Chất Của Hình Vuông
-
Hình Vuông Có Mấy Tính Chất Của đường Chéo