Đường Tiệm Cận Của đồ Thị Hàm Số: Lý Thuyết Và Cách Tìm ... - Marathon

Warning: mysqli_query(): (HY000/1): Can't create/write to file '/tmp/#sql-temptable-b851-b9aaf-17d5.MAI' (Errcode: 28 "No space left on device") in /opt/bitnami/wordpress/wp-includes/wp-db.php on line 2162

Trong chương trình toán học 12 thì đường tiệm cận là khái niệm mới mà các em học sinh cần phải sử dụng nhiều để giải các bài toán. Vậy đường tiệm cận là gì? Cách tìm đường tiệm cận như thế nào? Cùng Team Marathon Education theo dõi và tìm hiểu ngay qua bài viết dưới đây.

>>> Xem thêm: Đạo Hàm Là Gì? Các Công Thức Tính Đạo Hàm Thường Gặp

Khái niệm đường tiệm cận của đồ thị hàm số

Ta có: Cho đường thẳng y = f(x) có đồ thị C:

Đường tiệm cận đứng

Đồ thị C có đường tiệm cận đứng là x = a nếu như f(x) thỏa mãn được 1 trong 4 điều kiện sau:

\begin{aligned} &\lim\limits_{x\to a^+}f(x)=+\infin\\ &\lim\limits_{x\to a^+}f(x)=-\infin\\ &\lim\limits_{x\to a^-}f(x)=+\infin\\ &\lim\limits_{x\to a^-}f(x)=-\infin\\ \end{aligned}

Đường tiệm cận ngang

Đường thẳng y = b sẽ là tiệm cận ngang của đồ thị (C) nếu thỏa mãn ít nhất một trong các điều kiện sau:

\begin{aligned} &\lim\limits_{x\to +\infin}f(x)=b\\ &\lim\limits_{x\to-\infin}f(x)=b\\ \end{aligned}

Lưu ý: Đối với hàm số đa thức thì không có đường tiệm cận ngang và đường tiệm cận đứng. Do đó, đối với các bài toán dạng này các em không cần thực hiện tìm các đường tiệm cận này.

Đường tiệm cận xiên

Đường thẳng y = ax + b (a ≠ 0) được gọi là đường tiệm xiên của đồ thị (C) nếu như đường thẳng này thỏa mãn được ít nhất một trong 2 điều kiện dưới đây:

\begin{aligned} \left[ \begin{array}{c} \lim\limits_{x\to +\infin}[f(x)-(ax+b)]=0\\\lim\limits_{x\to -\infin}[f(x)-(ax+b)]=0 \end{array}\right. \end{aligned}

Trong đó:

\begin{cases} a=\lim\limits_{x\to +\infin}\frac{f(x)}{x}\\ b=\lim\limits_{x\to +\infin}[f(x)-ax] \end{cases} \text{ hoặc } \begin{cases} a=\lim\limits_{x\to -\infin}\frac{f(x)}{x}\\ b=\lim\limits_{x\to -\infin}[f(x)-ax] \end{cases}

>>> Xem thêm: Cách Tính Đạo Hàm Hàm Hợp Và Bài Tập Ứng Dụng

ĐĂNG KÝ NGAY

Cách tìm đường tiệm cận và các dạng bài tập

Đối với mỗi dạng hàm số khác nhau sẽ có những phương pháp giải tìm đường tiệm cận riêng. Dưới đây là hướng dẫn cách để tìm đường tiệm cận chi tiết và dễ hiểu nhất mà các em có thể áp dụng đối với 3 dạng toán: Tìm đường tiệm cận của hàm số phân thức bậc nhất, hàm số phân thức hữu tỉ và hàm số căn thức:

Cách Tính Đạo Hàm Cos2x Và Bài Tập Vận Dụng Có Đáp Án

Dạng 1: Tìm đường tiệm cận của hàm số phân thức bậc nhất

Phương pháp giải 

Cho hàm số phân thức bậc nhất:

y=\frac{ax+b}{cx+d} \begin{aligned} &\small\text{Để hàm số trên tồn tại các đường tiệm cận thì hàm số phải thỏa mãn điều kiện: } c ≠ 0 \text{ và } ad\ – \ bc ≠ 0\\ &\small\text{Khi đó ta sẽ được các đường tiệm cận đứng }x=-\frac{d}{c} \text{ và đường tiệm cận ngang }y=\frac{a}{c}. \end{aligned}

Ví dụ: Xác định đường tiệm cận đứng và tiệm cận ngang của hàm số:

y=\frac{2x-1}{x+2}

Giải:

\begin{aligned} &\small\text{TXĐ: } D=\R \setminus \{-2\}\\ &\small\text{Ta có: }\\ &\lim\limits_{x\to -\infin}y=\lim\limits_{x\to -\infin}\frac{2x-1}{x+2}=2\\ &\lim\limits_{x\to +\infin}y=\lim\limits_{x\to +\infin}\frac{2x-1}{x+2}=2\\ &\small\text{Vậy hàm số trên có đường tiệm cận ngang là }y = 2.\\ &\small\text{Ta có: }\\ &\lim\limits_{x\to (-2)^-}y=\lim\limits_{x\to (-2)^-}\frac{2x-1}{x+2}=-\infin\\ &\lim\limits_{x\to (-2)^+}y=\lim\limits_{x\to (-2)^+}\frac{2x-1}{x+2}=+\infin\\ &\small\text{Vậy hàm số trên có đường tiệm cận đứng là }x = -2. \end{aligned}

Kết luận: Đồ thị hàm số hàm số đã cho có đường tiệm cận ngang là y = 2 và đường tiệm cận đứng là x = -2.

Dạng 2: Tìm đường tiệm cận của hàm số phân thức hữu tỉ

Phương pháp giải

\begin{aligned} &\small \text{Tìm đường tiệm cận của đồ thị hàm số }y=\frac{A}{f(x)} \text{ với A là số thực khác 0 và f(x) là đa thức bậc n}\\ &\small \text{(n> 0).}\\ &\small \bull\text{Đồ thị hàm số } y=\frac{A}{f(x)} \text{ luôn có một tiệm cận ngang y = 0.}\\ &\small \bull\text{Tiệm cận đứng của hàm số } y=\frac{A}{f(x)} \text{là } x = x_0 \text{ nếu như thỏa mãn điều kiện }x_0 \text{ là nghiệm của}\\ &\small \text{đa thức }f(x) \text{ hay } f(x) = 0.\\ &\small \bull\text{Tiệm cận của }y=\frac{f(x)}{g(x)} \end{aligned}

TH2:

\begin{aligned} &\small \text{Tìm đường tiệm cận của đồ thị hàm số }y=\frac{f(x)}{g(x)}, \text{trong đó f(x) và g(x) là các đa thức bậc khác 0.}\\ &\small \bull\text{Hàm số } y=\frac{f(x)}{g(x)} \text{có tiệm cận ngang nếu như thỏa mãn điều kiện bậc đa thức f(x) nhỏ hơn bậc }\\ &\small \text{của đa thức g(x).}\\ &\small \bull\text{Để đường thẳng }x = x_0 \text{ trở thành tiệm cận đứng của đồ thị hàm số }y=\frac{f(x)}{g(x)} \text{ thì }x_0 \text{ phải là }\\ &\small \text{ nghiệm của g(x) nhưng không phải của f(x) hoặc đồng thời }x_0 \text{ là nghiệm}\\ &\small \text{bội n của g(x) và nghiệm bội m của f(x) }(m < n). \end{aligned}

Ví dụ: Tìm tiệm cận ngang và tiệm cận đứng của hàm số

y=\frac{x^2-x+1}{x-1}

Giải:

Lý Thuyết Toán 10 Phương Trình Đường Thẳng

\begin{aligned} &\small\text{TXĐ: } D=\R \setminus \{1\}\\ &\small\text{Ta có: }\\ &\lim\limits_{x\to +\infin}y=\lim\limits_{x\to +\infin}\frac{x^2-x+1}{x-1}=+\infin\\ &\lim\limits_{x\to -\infin}y=\lim\limits_{x\to -\infin}\frac{x^2-x+1}{x-1}=-\infin\\ &\small\text{Vậy hàm số trên không có đường tiệm cận ngang.}\\ &\small\text{Ta có: }\\ &\lim\limits_{x\to 1^+}y=\lim\limits_{x\to 1^+}\frac{x^2-x+1}{x-1}=+\infin\\ &\lim\limits_{x\to 1^-}y=\lim\limits_{x\to 1^-}\frac{x^2-x+1}{x-1}=-\infin\\ &\small\text{Vậy hàm số trên có đường tiệm cận đứng là }x = 1 \end{aligned}

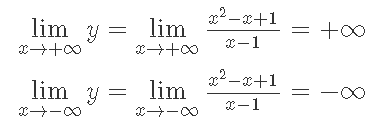
Kết luận: Đồ thị hàm số có đường tiệm cận đứng là x = 1.

Dạng 3: Tìm đường tiệm cận của hàm số căn thức

Phương pháp giải:

Cho hàm số y = f(x) với f(x) là hàm số chứa căn.

Tìm tập xác định D của f(x)

Để hàm số y = f(x) có tồn tại tiệm cận ngang thì:

\begin{aligned} &\small\bull \text{Trong tập xác định D của hàm số phải chứa ít nhất một trong hai kí hiệu -∞ hoặc +∞ }\\ &\small\bull \text{Một trong 2 giới hạn }\lim\limits_{x\to -\infin}y \text{ hoặc }\lim\limits_{x\to +\infin}y \text{ hữu hạn.} \end{aligned}

Ví dụ 1: Xác định tiệm cận ngang và tiệm cận đứng của hàm số

y=\frac{\sqrt{x^2+1}}{x}

Giải: 

\begin{aligned} &\small\text{TXĐ: } D=\R \setminus \{0\}\\ &\small\text{Ta có: }\\ &\lim\limits_{x\to +\infin}y=\lim\limits_{x\to +\infin}\frac{\sqrt{x^2+1}}{x}=-1\\ &\lim\limits_{x\to -\infin}y=\lim\limits_{x\to -\infin}\frac{\sqrt{x^2+1}}{x}=-1\\ &\small\text{Vậy đường thẳng }y = -1 \text{ là tiệm cận ngang của đồ thị hàm số.}\\ &\small\text{Ta có: }\\ &\lim\limits_{x\to 0^+}y=\lim\limits_{x\to 0^+}\frac{\sqrt{x^2+1}}{x}=+\infin\\ &\lim\limits_{x\to 0^-}y=\lim\limits_{x\to 0^-}\frac{\sqrt{x^2+1}}{x}=-\infin\\ &\small\text{Vậy hàm số trên có đường tiệm cận đứng là }x = 0 \end{aligned}

Ví dụ 2: Xac định tiệm cận ngang và tiệm cận đứng của hàm số

y=1+\sqrt{1-x^2}

Giải: 

Ta có:

y=1+\sqrt{1-x^2} \Leftrightarrow\begin{cases}-1 \le x\le 1\\ y\ge 1 \\ x^2+(y-1)^2=1\end{cases}

Vậy đồ thị hàm số là nửa đường tròn bán kính R = 1, tâm I(0;1) nên đồ thị không có đường tiệm cận.

>>> Xem thêm: Lý Thuyết Toán 12 Cực Trị Của Hàm Số Và Phương Pháp Tìm Cực Trị

Tham khảo ngay các khoá học online của Marathon Education

Gia sư Online Công Thức Tính Đạo Hàm Căn Bậc 3 Và Một Số Ví Dụ Minh Họa Học Online Toán 12 Học Online Hóa 10 Học Online Toán 11 Học Online Toán 6 Học Online Toán 10 Học Online Toán 7 Học Online Lý 10 Học Online Lý 9 Học Online Toán 8 Học Online Toán 9 Học Tiếng Anh 6 Học Tiếng Anh 7

Trên đây là chia sẻ của Team Marathon Education về kiến thức toán học 12 đường tiệm cận và các phương pháp giải dễ hiểu nhất. Hi vọng qua bài viết này các em sẽ nắm rõ hơn được kiến thức và áp dụng vào các bài toán của mình thành công. Chúc các em đạt nhiều thành tích cao trong học tập.

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!