Giải Bài 1 Trang 18 SGK Giải Tích 12
Có thể bạn quan tâm
LG a
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :
\(y{\rm{ }} = {\rm{ }}2{x^{3}} + {\rm{ }}3{x^2}-{\rm{ }}36x{\rm{ }}-{\rm{ }}10\) ;
Phương pháp giải:
Quy tắc 1 tìm cực trị của hàm số:
Bước 1: Tìm tập xác định.
Bước 2: Tính \(f'\left( x \right)\). Tìm các điểm mà tại đó \(f'\left( x \right)\) bằng 0 hoặc \(f'\left( x \right)\) không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Lời giải chi tiết:
Tập xác định: \(D = \mathbb R\)
\(\eqalign{& y' = 6{{\rm{x}}^2} + 6{\rm{x}} - 36;y' = 0 \cr & \Leftrightarrow \left[ \matrix{x = 2\Rightarrow {y = - 54} \hfill \cr x = - 3 \Rightarrow {y = 71} \hfill \cr} \right. \cr} \)
\(\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( { - 3;2} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( {2; + \infty } \right)\end{array}\)
\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
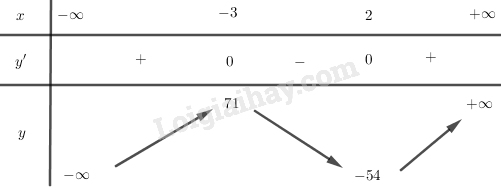
Bảng biến thiên:
Hàm số đạt cực đại tại \(x = -3\) và \(y\)CĐ \(= 71\)
Hàm số đạt cực tiểu tại \(x = 2\) và \(y\)CT \(= -54\)
Từ khóa » Cực Trị Của Hàm Số Bài Tập Trang 18
-
Giải Bài 1 Trang 18 Sgk Giải Tích 12
-
Giải Bài 2 Trang 18 Sgk Giải Tích 12
-
Giải Bài Tập Trang 18 SGK Giải Tích 12 Bài 1, 2, 3, 4, 5, 6 - Cực Trị
-
Bài 1,2,3,4,5,6 Trang 18 SGK Giải Tích Lớp 12 ( Bài Tập Cực Trị Hàm Số )
-
Cực Trị Của Hàm Số - Giải Toán 12 Trang 18
-
Giải Bài Tập Trang 18 SGK Giải Tích Lớp 12: Cực Trị Của Hàm Số
-
Bài Tập 1 Trang 18 SGK Giải Tích 12 (Cực Trị Của Hàm Số) (a,b,c)
-
Hướng Dẫn Giải Bài 1 2 3 4 5 6 Trang 18 Sgk Giải Tích 12
-
Giải Bài 1 Trang 18 – SGK Môn Giải Tích Lớp 12 - Chữa Bài Tập
-
Giải Bài Tập Cực Trị Của Hàm Số Lớp 12 (Hay Nhất)
-
Giải Bài 1, 2, 3 Trang 18 SGK Giải Tích 12
-
Bài Tập 6 Trang 18 SGK Giải Tích 12 (Cực Trị Của Hàm Số)
-
Áp Dụng Quy Tắc 1, Hãy Tìm Các điểm Cực Trị Của Các Hàm Số Sau
-
Hướng Dẫn Giải Bài Tập Giải Tích 12 Trang 18 Sách Giáo Khoa