Giải Bài 9, 10, 11 Trang 59, 60 Sách Giáo Khoa Hình Học 10

Bài 9 trang 59 sgk hình học 10

Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng :

$${m^2} + {n^2} = 2({a^2} + {b^2})$$

Giải

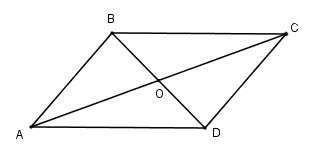
Áp dụng định lí về đường trung tuyến:

\(OA^2 =\frac{AD^{2}+AB ^{2}}{2} - \frac{BD^{2}}{4}\)

Thay \(OA = \frac{n}{2}, AB = a\)

\(AD = BC = b\) và \(BD = m\)

\({\left( {{n \over 2}} \right)^2} = {{{b^2} + {a^2}} \over 2} - {{{m^2}} \over 4} \Rightarrow {n^2} = 2{b^2} + 2{a^2} - {m^2} \)

\(\Rightarrow {m^2} + {n^2} = 2({a^2} + {b^2})\)

 

Bài 10 trang 60 sgk hình học 10

Hai chiếc tàu thủy \(P\) và \(Q\) cách nhau \(300m\).Từ \(P\) và \(Q\) thẳng hàng với chân \(A\) của tháp hải đăng \(AB\) ở trên bờ biển người ta nhìn chiều cao \(AB\) của tháp dưới các góc \(\widehat {BPA} = {35^0},\widehat {BQA} = {48^0}\)

Tính chiều cao của tháp.

Giải

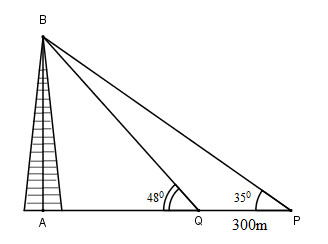
Ta có: \(AQ = AB\cot48^0\) 

\(AP = AB\cot35^0\) 

\(QP = AB(cot35^0- cot48^0)\) 

\(AB = {{300} \over {\cot {{35}^0} - \cot {{48}^0}}} \approx {{300} \over {1,4281 - 0,9004}} \approx 568,457m\)

 

Bài 11 trang 60 sgk hình học 10

 Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12cm\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3cm\). Gọi \(D\) là đỉnh tháp và hai điểm \(A_1,B_1\) cùng thẳng  hàng với \(C_1\) thuộc chiều cao \(CD\) của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^0}\) và \(\widehat {D{B_1}{C_1}} = {35^0}\)

Tính chiều cao của  \(CD\) của tháp đó.

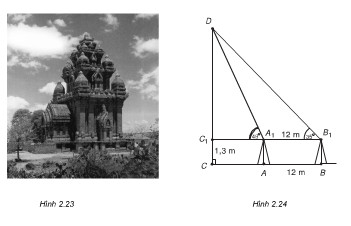
Giải

Ta có: Chiều cao của tháp \(DC = DC_1+ C_1C = 1,3 + DC_1\)

\(DC = 1,3 + {{12} \over {\cot {{35}^0} - \cot {{49}^0}}} \approx 22,8m\)

 

Giaibaitap.me