Giải Bài Tập Toán 10 SBT Bài 3 Chương 2 - Hàm Số Bậc Hai

Có thể bạn quan tâm

- - Mầm non
  - Lớp 1
  - Lớp 2
  - Lớp 3
  - Lớp 4
  - Lớp 5
  - Lớp 6
  - Lớp 7
  - Lớp 8
  - Lớp 9
  - Lớp 10
  - Lớp 11
  - Lớp 12
  - Thi vào lớp 6
  - Thi vào lớp 10
  - Thi Tốt Nghiệp THPT
  - Đánh Giá Năng Lực
  - Khóa Học Trực Tuyến
  - Hỏi bài
  - Trắc nghiệm Online
  - Tiếng Anh
  - Thư viện Học liệu
  - Bài tập Cuối tuần
  - Bài tập Hàng ngày
  - Thư viện Đề thi
  - Giáo án - Bài giảng
  - Tất cả danh mục
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 10 Giải Vở BT Toán 10 Giải bài tập Toán 10 SBT bài 3 chương 2 Hàm số bậc hai Bài trước Tải về Bài sau Lớp: Lớp 10 Môn: Toán Dạng tài liệu: Giải bài tập Loại File: PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Toán 10 - Hàm số bậc hai

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 3 chương 2, tài liệu gồm 6 bài tập trang 40 kèm theo đáp án sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán 10 một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT bài 5 chương 1

Giải bài tập Toán 10 SBT ôn tập chương 1

Giải bài tập Toán 10 SBT bài 1 chương 2

Giải bài tập Toán 10 SBT bài 2 chương 2

Giải bài tập Toán 10 SBT bài 3

Bài 14 trang 40 Sách bài tập (SBT) Toán Đại số 10

Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.

a) y=2x2−x−2

b) y=−2x2−x+2

c) $y = - {1 \over 2}{x^2} + 2x - 1$ $y = - {1 \over 2}{x^2} + 2x - 1$

d) $y = - {1 \over 2}{x^2} + 2x - 1$ $y = - {1 \over 2}{x^2} + 2x - 1$

Gợi ý làm bài

a) Ở đây $a = 2;b = - 2;c = - 2$. Ta có $\Delta = {( - 1)^2} - 4.2.( - 2) = 17$ $\Delta = {( - 1)^2} - 4.2.( - 2) = 17$

Trục đối xứng là đường thẳng $x = {1 \over 4}$ $x = {1 \over 4}$ ; đỉnh $I({1 \over 4}; - {{17} \over 8})$ $I({1 \over 4}; - {{17} \over 8})$ giao với trục tung tại điểm (0;-2).

Để tìm giao điểm với trục hoành ta giải phương trình

$2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = {{1 \pm \sqrt {17} } \over 4}$ $2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = {{1 \pm \sqrt {17} } \over 4}$

Vậy các giao điểm với trục hoành là $({{1 + \sqrt {17} } \over 4};0 )$ $({{1 + \sqrt {17} } \over 4};0 )$ và $({{1 - \sqrt {17} } \over 4};0 )$ $({{1 - \sqrt {17} } \over 4};0 )$

b) Trục đối xứng $x = - {1 \over 4}$ $x = - {1 \over 4}$ ; đỉnh $I( - {1 \over 4}; - {{17} \over 8})$ $I( - {1 \over 4}; - {{17} \over 8})$ giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm $( - {{1 + \sqrt {17} } \over 4};0)$ $( - {{1 + \sqrt {17} } \over 4};0)$ và $({{\sqrt {17} - 1} \over 4};0)$ $({{\sqrt {17} - 1} \over 4};0)$

c) Trục đối xứng x = 2; đỉnh I(2;1); giao với trục tung tại điểm (0;-1) giao với trục hoành tại các điểm $(1 + \sqrt 2 ;0)$ $(1 + \sqrt 2 ;0)$ và $(2 - \sqrt 2 ;0)$ $(2 - \sqrt 2 ;0)$

d) Trục đối xứng x = 5; đỉnh I(5;1); giao với trục tung tại điểm (0;6). Parabol không cắt trục hoành $(\Delta = - {4 \over 5} < 0)$ $(\Delta = - {4 \over 5} < 0)$

Bài 15 trang 40 Sách bài tập (SBT) Toán 10

Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai

a) $y = 2{x^2} + 4x - 6$ $y = 2{x^2} + 4x - 6$

b) $y = - 3{x^2} - 6x + 4$ $y = - 3{x^2} - 6x + 4$

c) $y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2$ $y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2$

d) $y = - 2({x^2} + 1)$ $y = - 2({x^2} + 1)$

Gợi ý làm bài

a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;

Vậy $- {b \over {2a}} = - 1;\Delta = {b^2} - 4ac = 64; - {\Delta \over {4a}} = - 8$ $- {b \over {2a}} = - 1;\Delta = {b^2} - 4ac = 64; - {\Delta \over {4a}} = - 8$

Vì a > 0, ta có bảng biến thiên

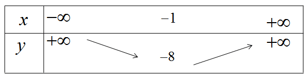
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số nghịch biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$ đồng biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$

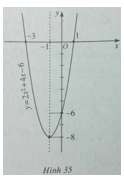
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).

Đồ thị của hàm số $y = 2{x^2} + 4x - 6$ $y = 2{x^2} + 4x - 6$ được vẽ trên hình 35.

Giải bài tập Toán 10 SBT bài 3 chương 2

b) Bảng biến thiên

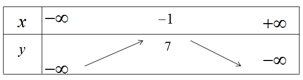
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số đồng biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$ và nghịch biến trên khoảng $( - 1; + \infty )$ $( - 1; + \infty )$

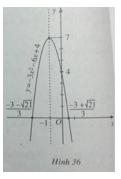
Đỉnh parabol I(-1;7). Đồ thị của hàm số $y = - 3{x^2} - 6x + 4$ $y = - 3{x^2} - 6x + 4$ được vẽ trên hình 36.

Giải bài tập Toán 10 SBT bài 3 chương 2

c) Bảng biến thiên

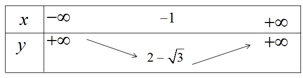
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số nghịch biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$ và đồng biến trên khoảng $( - 1; + \infty )$ $( - 1; + \infty )$

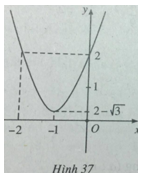
Đỉnh parabol $( - 1;2 - \sqrt 3 )$ $( - 1;2 - \sqrt 3 )$

Đồ thị hàm số được vẽ trên hình 37.

Giải bài tập Toán 10 SBT bài 3 chương 2

d) $y = - 2{x^2} - 2$ $y = - 2{x^2} - 2$

Bảng biến thiên

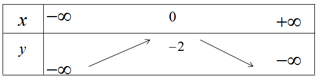
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số đồng biến trên khoảng $( - \infty ;0)$ $( - \infty ;0)$ và nghịch biến trên khoảng $(0; + \infty )$ $(0; + \infty )$, hàm số là chẵn.

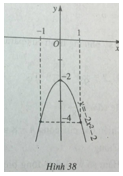
Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).

Đồ thị hàm số $y = - 2({x^2} + 1)$ $y = - 2({x^2} + 1)$ được vẽ trên hình 38.

Giải bài tập Toán 10 SBT bài 3 chương 2

Bài 16 trang 40 Sách bài tập (SBT) Toán Đại số 10

Xác định hàm số bậc hai y=ax2−4x+c, biết rằng đồ thị của nó

a) Đi qua hai điểm A(1;-2) và B(2;3);

b) Có đỉnh là I(-2 ;-1) ;

c) Có hoành độ đỉnh là -3 và đi qua điểm P(-2 ;1) ;

d) Có trục đối xứng là đường thẳng x = 2 và cắt trục hoành tại điểm M(3 ;0).

Gợi ý làm bài

Các hàm số bậc hai cần xác định đều có b = -4.

a) Ta có

Giải bài tập Toán 10 SBT bài 3 chương 2

Vậy hàm số cần tìm là $y = 3{x^2} - 4x - 1$ $y = 3{x^2} - 4x - 1$

b) $y = - {x^2} - 4x - 5$ $y = - {x^2} - 4x - 5$

c) $y = - {2 \over 3}{x^2} - 4x - {{13} \over 3}$ $y = - {2 \over 3}{x^2} - 4x - {{13} \over 3}$

d) $y = {x^2} - 4x + 3$ $y = {x^2} - 4x + 3$

Bài 17 trang 40 Sách bài tập (SBT) Toán Đại số 10

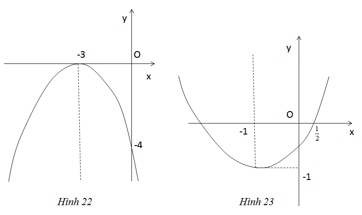
Viết phương trình của parabol $y = a{x^2} + bx + c$ $y = a{x^2} + bx + c$ ứng với mỗi đồ thị dưới đây

Giải bài tập Toán 10 SBT bài 3 chương 2

Gợi ý làm bài

a) Dựa trên đồ thị (h.22) ta thấy parabol có đỉnh I(-3 ;0) và đi qua điểm (0 ;-4). Như vậy

$c = - 4; - {b \over {2a}} = - 3 \Leftrightarrow b = 6a$ $c = - 4; - {b \over {2a}} = - 3 \Leftrightarrow b = 6a$ Thay c = -4 và b = 6a vào biểu thức

$\Delta = {b^2} - 4ac = 0 = > 36{a^2} + 16a = 0 = > a = - {4 \over 9}$ $\Delta = {b^2} - 4ac = 0 = > 36{a^2} + 16a = 0 = > a = - {4 \over 9}$ vì a ≠ 0 và $b = - {8 \over 3}$ $b = - {8 \over 3}$

Vậy phương trình của parabol là $y = - {4 \over 9}{x^2} - {8 \over 3}x - 4$ $y = - {4 \over 9}{x^2} - {8 \over 3}x - 4$

b) $y = {4 \over 9}{x^2} + {8 \over 9}x - {5 \over 9}$ $y = {4 \over 9}{x^2} + {8 \over 9}x - {5 \over 9}$

Bài 18 trang 40 Sách bài tập (SBT) Toán Đại số 10

Một chiếc ăng – ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4 m. Ở mặt cắt qua trục ta được một parabol dạng y=ax2 (h.24). Hãy xác định hệ số a.

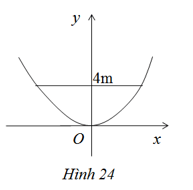
Giải bài tập Toán 10 SBT bài 3 chương 2

Gợi ý làm bài

Ta có thiết diện mặt cắt qua trục của chiếc ăng-ten là:

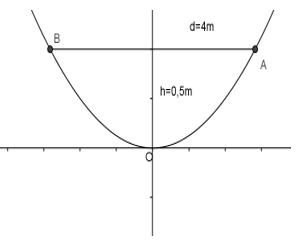
Giải bài tập Toán 10 SBT bài 3 chương 2

Vậy ta có: $A\left( {2;{1 \over 2}} \right)$ $A\left( {2;{1 \over 2}} \right)$ mà $A \in prapol: y = ax_{}^2 \Rightarrow {1 \over 2} = a.2_{}^2 \Leftrightarrow a = {1 \over 8}$ $A \in prapol: y = ax_{}^2 \Rightarrow {1 \over 2} = a.2_{}^2 \Leftrightarrow a = {1 \over 8}$

Bài 19 trang 40 Sách bài tập Toán 10

Một chiếc cổng hình parabol dạng $y = - {1 \over 2}{x^2}$ $y = - {1 \over 2}{x^2}$có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).

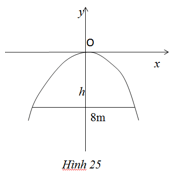
Giải bài tập Toán 10 SBT bài 3 chương 2

Gợi ý làm bài

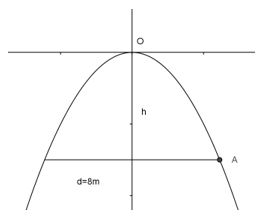
Giải bài tập Toán 10 SBT bài 3 chương 2

Ta có: $A\left( {4; - h} \right)$ $A\left( {4; - h} \right)$ mà $A \in parabol y = - {1 \over 2}x_{}^2 \Rightarrow h = \left| { - {1 \over 2}.4_{}^2} \right| \Rightarrow h = 8$ $A \in parabol y = - {1 \over 2}x_{}^2 \Rightarrow h = \left| { - {1 \over 2}.4_{}^2} \right| \Rightarrow h = 8$

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Tải về Chọn file muốn tải về:

Giải bài tập Toán 10 SBT bài 3 chương 2

256,3 KB

Giải bài tập Toán 10 SBT bài 3 chương 2 .DOC
342,5 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này! Đóng 79.000 / tháng Mua ngay Đặc quyền các gói Thành viên PRO Phổ biến nhất PRO+ Tải tài liệu Cao cấp 1 Lớp 30 lượt tải tài liệu Xem nội dung bài viết Trải nghiệm Không quảng cáo Làm bài trắc nghiệm không giới hạn Tìm hiểu thêm Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi: Phan Thị Hoàn

3 618 Bài viết đã được lưu Bài trước Mục lục Bài sau

Tham khảo thêm

Giải bài tập Toán 10 SBT bài 1 chương 6
Giải bài tập Toán 10 SBT bài 2 chương 6
Giải bài tập Toán 10 SBT bài 3 chương 5
Giải bài tập Toán 10 SBT bài 3 chương 6
Giải bài tập Toán 10 SBT ôn tập chương 5
Giải bài tập Toán 10 SBT bài 4 chương 5
Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học
Giải bài tập Toán 10 SBT ôn tập chương 6
Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học
Giải bài tập Toán 10 SBT ôn tập cuối năm

Giải Vở BT Toán 10

Giải bài tập Toán 10 SBT bài 3 chương 6
Giải bài tập Toán 10 SBT ôn tập chương 6
Giải bài tập Toán 10 SBT ôn tập cuối năm
Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học
Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học
Giải bài tập Toán 10 SBT bài 2 chương 6

Xem thêm

Gợi ý cho bạn

TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4
Được 18-20 điểm khối A1 nên đăng ký trường nào?
Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1
Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao

Xem thêm

Từ khóa » Hàm Số Bậc Hai Lớp 10 Sbt

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Toán 10 - Hàm số bậc hai

Giải bài tập Toán 10 SBT bài 3

Giải bài tập Toán 10 SBT bài 3 chương 2

Giải bài tập Toán 10 SBT bài 3 chương 2 .DOC

Có thể bạn quan tâm

Chương 1: Mệnh đề - Tập hợp

Chương 2: Hàm số bậc nhất và bậc hai

Chương 3: Phương trình. Hệ phương trình

Chương 4: Bất đẳng thức. Bất phương trình

Chương 5: Thống kê

Chương 6: Cung và góc lượng giác. Công thức lượng giác

Hình học 10

Lớp 10

Giải Vở BT Toán 10

Đề thi khảo sát chất lượng đầu năm lớp 10

Đề thi giữa kì 1 lớp 10

Đề thi học kì 1 lớp 10

Đề thi giữa kì 2 lớp 10

Đề thi học kì 2 lớp 10

Thi học sinh giỏi lớp 10

Đề kiểm tra 15 phút lớp 10

Toán lớp 10

Toán 10 Kết nối tri thức

Toán 10 Chân trời sáng tạo

Toán 10 Cánh Diều

Lý thuyết Toán 10 KNTT

Lý thuyết Toán 10 CTST

Tham khảo thêm

Giải bài tập Toán 10 SBT bài 1 chương 6

Giải bài tập Toán 10 SBT bài 2 chương 6

Giải bài tập Toán 10 SBT bài 3 chương 5

Giải bài tập Toán 10 SBT bài 3 chương 6

Giải bài tập Toán 10 SBT ôn tập chương 5

Giải bài tập Toán 10 SBT bài 4 chương 5

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

Giải bài tập Toán 10 SBT ôn tập chương 6

Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

Giải bài tập Toán 10 SBT ôn tập cuối năm

Giải Vở BT Toán 10

Giải bài tập Toán 10 SBT bài 3 chương 6

Giải bài tập Toán 10 SBT ôn tập chương 6

Giải bài tập Toán 10 SBT ôn tập cuối năm

Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

Giải bài tập Toán 10 SBT bài 2 chương 6

Gợi ý cho bạn

TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4

Được 18-20 điểm khối A1 nên đăng ký trường nào?

Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1

Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao

Liên Hệ