Giải Bài Tập Toán 11 Bài 4: Cấp Số Nhân

Có thể bạn quan tâm

- - Mầm non
  - Lớp 1
  - Lớp 2
  - Lớp 3
  - Lớp 4
  - Lớp 5
  - Lớp 6
  - Lớp 7
  - Lớp 8
  - Lớp 9
  - Lớp 10
  - Lớp 11
  - Lớp 12
  - Thi vào lớp 6
  - Thi vào lớp 10
  - Thi Tốt Nghiệp THPT
  - Đánh Giá Năng Lực
  - Khóa Học Trực Tuyến
  - Hỏi bài
  - Trắc nghiệm Online
  - Tiếng Anh
  - Thư viện Học liệu
  - Bài tập Cuối tuần
  - Bài tập Hàng ngày
  - Thư viện Đề thi
  - Giáo án - Bài giảng
  - Tất cả danh mục
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 11 Giải bài tập Toán lớp 11 Giải bài tập Toán 11 bài 4: Cấp số nhân Giải bài tập môn Toán lớp 11 Tải về Lớp: Lớp 11 Môn: Toán Dạng tài liệu: Giải bài tập Loại File: PDF + Word Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Giải bài tập Toán 11 Giải tích: Cấp số nhân

Bài 1 trang 103 SGK Đại số 11
Bài 2 trang 103 SGK Đại số 11
Bài 3 trang 103 SGK Đại số 11
Bài 4 trang 104 SGK Đại số 11
Bài 5 trang 104 SGK Đại số 11
Bài 6 trang 104 SGK Đại số 11

VnDoc xin giới thiệu tới bạn đọc bộ tài liệu Giải bài tập Toán 11 bài 4: Cấp số nhân, nội dung tài liệu gồm 6 bài tập trang 103, 104 SGK Toán 11 kèm theo lời giải chi tiết sẽ giúp các bạn học sinh giải nhanh bài tập một cách hiệu quả nhất. Mời thầy cô cùng các bạn học sinh cùng tham khảo.

Giải bài tập Toán 11 Cấp số nhân

Bài 1 trang 103 SGK Đại số 11

Chứng minh các dãy số $\left( \frac{3}{5}{{.2}^{n}} \right);\left( \frac{5}{{{2}^{n}}} \right);{{\left( \frac{-1}{2} \right)}^{n}}$ $\left( \frac{3}{5}{{.2}^{n}} \right);\left( \frac{5}{{{2}^{n}}} \right);{{\left( \frac{-1}{2} \right)}^{n}}$ là các cấp số nhân.

Hướng dẫn giải

$u_n$ là cấp số nhân $\Rightarrow$ $\Rightarrow$ $u_{n+1}=u_n.q$ $u_{n+1}=u_n.q$ với $n \in \mathbb{N}^*$ $n \in \mathbb{N}^*$

Công bội $q=\dfrac{u_{n+1}}{u_n}$ $q=\dfrac{u_{n+1}}{u_n}$

Lời giải:

Để chứng minh dãy (un) là cấp số nhân thì ta chứng minh:

un+1 = un.q với n ∈ N*

(q là công bội cấp số nhân)

${{u}_{n}}=\frac{3}{5}{{.2}^{n}}$ ${{u}_{n}}=\frac{3}{5}{{.2}^{n}}$

Xét $\frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{\frac{3}{5}{{.2}^{n+1}}}{\frac{3}{5}{{.2}^{n}}}=\frac{{{2}^{n+1}}}{{{2}^{n}}}=\frac{{{2}^{n}}.2}{{{2}^{n}}}=2$ $\frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{\frac{3}{5}{{.2}^{n+1}}}{\frac{3}{5}{{.2}^{n}}}=\frac{{{2}^{n+1}}}{{{2}^{n}}}=\frac{{{2}^{n}}.2}{{{2}^{n}}}=2$

=> un+1 = 2 x un. Vậy $u_n$ là cấp số nhân với công bội q = 2.

${{u}_{n}}=\frac{5}{{{2}^{n}}}$ ${{u}_{n}}=\frac{5}{{{2}^{n}}}$

Với $n\in {{\mathbb{N}}^{*}}\Rightarrow {{u}_{n}}>0$ $n\in {{\mathbb{N}}^{*}}\Rightarrow {{u}_{n}}>0$

Xét $\frac{{{u}_{n+1}}}{{{u}_{n}}}=\dfrac{\dfrac{5}{{{2}^{n+1}}}}{\dfrac{5}{{{2}^{n}}}}=\dfrac{1}{2}\Rightarrow {{u}_{n+1}}=\dfrac{1}{2}{{u}_{n}}$ $\frac{{{u}_{n+1}}}{{{u}_{n}}}=\dfrac{\dfrac{5}{{{2}^{n+1}}}}{\dfrac{5}{{{2}^{n}}}}=\dfrac{1}{2}\Rightarrow {{u}_{n+1}}=\dfrac{1}{2}{{u}_{n}}$

Vậy $\left( {{u}_{n}} \right)$ $\left( {{u}_{n}} \right)$ là cấp số nhân với công bội $q=\frac{1}{2}$ $q=\frac{1}{2}$

${{u}_{n}}={{\left( \frac{-1}{2} \right)}^{n}}=\left( -1 \right).{{\left( \frac{1}{2} \right)}^{n}}\Leftrightarrow \frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{{{\left( -1 \right)}^{n+1}}{{\left( \frac{1}{2} \right)}^{n+1}}}{{{\left( -1 \right)}^{n}}{{\left( \frac{1}{2} \right)}^{n}}}$ ${{u}_{n}}={{\left( \frac{-1}{2} \right)}^{n}}=\left( -1 \right).{{\left( \frac{1}{2} \right)}^{n}}\Leftrightarrow \frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{{{\left( -1 \right)}^{n+1}}{{\left( \frac{1}{2} \right)}^{n+1}}}{{{\left( -1 \right)}^{n}}{{\left( \frac{1}{2} \right)}^{n}}}$

Xét $\frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{{{\left( -1 \right)}^{n}}.{{\left( -1 \right)}^{1}}.{{\left( \frac{1}{2} \right)}^{n+1}}}{{{\left( -1 \right)}^{n}}{{\left( \frac{1}{2} \right)}^{n}}}=\frac{-1}{2}\Rightarrow {{u}_{n+1}}=\frac{-1}{2}{{u}_{n}}$ $\frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{{{\left( -1 \right)}^{n}}.{{\left( -1 \right)}^{1}}.{{\left( \frac{1}{2} \right)}^{n+1}}}{{{\left( -1 \right)}^{n}}{{\left( \frac{1}{2} \right)}^{n}}}=\frac{-1}{2}\Rightarrow {{u}_{n+1}}=\frac{-1}{2}{{u}_{n}}$

Vậy $\left( {{u}_{n}} \right)$ $\left( {{u}_{n}} \right)$ là cấp số nhân với công bội $q=\frac{-1}{2},\forall n\in {{\mathbb{N}}^{*}}$ $q=\frac{-1}{2},\forall n\in {{\mathbb{N}}^{*}}$

Bài 2 trang 103 SGK Đại số 11

Cho cấp số nhân ($u_n$) với công bội q

a. Biết u1 = 2, u6 = 486. Tìm q

b. Biết q = 2/3 , u4 = 8/21. Tìm u1

c. Biết u1 = 3, q = -2. Hỏi số 192 là số hạng thứ mấy?

Hướng dẫn giải

Số hạng thứ n của cấp số nhân được tính bằng công thức $u_n=u_1.q^{n-1}$ $u_n=u_1.q^{n-1}$trong đó n là số nguyên thỏa mãn $n \ge1$ $n \ge1$

- Công bội khi đó là: $q=\left ( \dfrac{u_n}{u_1} \right ) ^{\frac{1}{n-1}}$ $q=\left ( \dfrac{u_n}{u_1} \right ) ^{\frac{1}{n-1}}$ hoặc $q=\sqrt[n-1]{\dfrac{u_n}{u_1}}$ $q=\sqrt[n-1]{\dfrac{u_n}{u_1}}$ trong đó n là số nguyên thỏa mãn $n \ge 1$ $n \ge 1$

Lời giải:

a. Theo công thức un = u1.qn-1, thay n = 6 ta được:

u6 = u1.q5 = 2.q5 = 486

q5 = 243 = 35 => q = 3

b. Ta có:

${{u}_{4}}={{u}_{1}}.{{q}^{4-1}}=\frac{8}{21}\Rightarrow \frac{8}{21}.{{\left( \frac{3}{2} \right)}^{n}}=\frac{27}{21}=\frac{9}{7}$ ${{u}_{4}}={{u}_{1}}.{{q}^{4-1}}=\frac{8}{21}\Rightarrow \frac{8}{21}.{{\left( \frac{3}{2} \right)}^{n}}=\frac{27}{21}=\frac{9}{7}$

c. Biết u1 = 3, q = -2. Hỏi số 192 là số thứ mấy?

Ta có: un = u1.qn-1 = 192

qn-1 = 192/u1 = 192/3 = 64

(-2)n = - 128 = (-2)7 => n = 7

Vậy số 192 là số hạng thứ 7.

Bài 3 trang 103 SGK Đại số 11

Tìm các số hạng của cấp số nhân ($u_n$) có năm số hạng, biết:

a. u3 = 3 và u5 = 27

b. u4 – u2 = 25 và u3 – u1 = 50

Hướng dẫn giải

Số hạng thứ n của cấp số nhân được tính bằng công thức $u_n=u_1.q^{n-1}$ $u_n=u_1.q^{n-1}$trong đó n là số nguyên thỏa mãn $n \ge1$ $n \ge1$

- Theo đề bài ra ta được hệ phương trình ẩn $u_1,q$. Giải hệ phương trình ta tìm được dãy số cần tìm. Thay n = 1, 2, 3, 4, 5 ta tìm được 5 số hạng đầu dãy.

Lời giải:

a. Ta có: un = u1qn-1

$\Rightarrow \left\{ \begin{matrix} {{u}_{3}}={{u}_{1}}.{{q}^{2}}=3 \\ {{u}_{5}}={{u}_{1}}.{{q}^{4}}=27 \\ \end{matrix}\Rightarrow \left\{ \begin{matrix} {{q}^{2}}=9 \\ {{u}_{1}}=\frac{1}{3} \\ \end{matrix} \right. \right.$ $\Rightarrow \left\{ \begin{matrix} {{u}_{3}}={{u}_{1}}.{{q}^{2}}=3 \\ {{u}_{5}}={{u}_{1}}.{{q}^{4}}=27 \\ \end{matrix}\Rightarrow \left\{ \begin{matrix} {{q}^{2}}=9 \\ {{u}_{1}}=\frac{1}{3} \\ \end{matrix} \right. \right.$

Vậy q = ± 3.

+ Cấp số nhân (un) có công bội q có thể viết dưới dạng:

u1, u1q, u1q2,…,u1.qn-1

Với q = 3 ta có cấp số: 1/3 , 1, 3, 9, 27

Với q = - 3 ta có cấp số: 1/3 , -1, 3, -9, 27

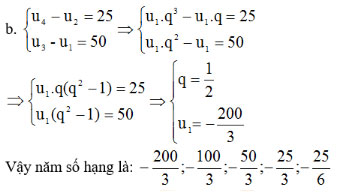
Giải bài tập Toán 11 Cấp số nhân

Bài 4 trang 104 SGK Đại số 11

Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62.

Hướng dẫn giải

Số hạng thứ n của cấp số nhân được tính bằng công thức $u_n=u_1.q^{n-1}$ $u_n=u_1.q^{n-1}$trong đó n là số nguyên thỏa mãn $n \ge1$ $n \ge1$.
Tổng n số hạng của cấp số nhân $S_n=\dfrac{u_1(1-q^n)}{1-q}$ $S_n=\dfrac{u_1(1-q^n)}{1-q}$
Áp dụng công thức trên ta được hệ phương trình ẩn $u_1,q$. Giải hệ phương trình ta tìm được cấp số nhân.

Lời giải:

Gọi u1, u2, u3, u4, u5, u6 là cấp số nhân của 6 số hạng.

+ Tổng của 5 số hạng đầu là 31 và 5 số hạng sau là 62, nghĩa là:

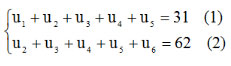
Giải bài tập Toán 11 Cấp số nhân

Ta có: (2) – (1) <=> u6 - u1 = 31

Mà u6 = u1.q6-1 = u1.q5

=> u1.q5 - u1 = 31 <=> u1(q5 – 1) = 31 (3)

Mặt khác, tổng của 5 số hạng đầu là:

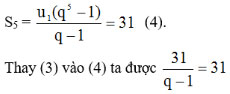
Giải bài tập Toán 11 Cấp số nhân

=> q – 1 = 1 => q = 2. Tính ra ta được u1 = 1.

Với un = u1qn-1

=> u2 = 2; u3 = 4, u4 = 8, u5 = 16, u6 = 32

Vậy cấp số nhân cần tìm là: 1, 2, 4, 8, 16, 32.

Bài 5 trang 104 SGK Đại số 11

Tỷ lệ tăng dân số của tỉnh x là 1,4%. Biết rằng dân số của tỉnh hiện nay là 1,8 triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm thì dân số của tỉnh đó tăng bao nhiêu?

Hướng dẫn giải

Cấp số nhân $(u_n)$ có số hạng đầu tiên $u_1$ và công bội q thì số hạng thứ n: $u_n=u_1.q^{n-1}$ $u_n=u_1.q^{n-1}$với mọi $n \ge 1$ $n \ge 1$

Lời giải:

Theo tỷ lệ tăng dân số 1,4% thì dân số hàng năm của tỉnh x là các số hạng của cấp số nhân với công bội q = 1 + 14/1000 = 1.014

Và số hạng đầu u1 = 1,8 triệu

Theo công thức: un = u1qn-1

=> Dân số của tỉnh x sau 5 năm sau là:

u6 = 1,8.(1.014)5 ≈ 1.9 triệu (người)

Vậy sân số sau 10 năm là: u11 = 1,8.(1.014)10 ≈ 2.1 triệu (người).

Bài 6 trang 104 SGK Đại số 11

Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C1 (hình bên). Từ hình vuông C2 lại tiếp tục như trên để được hình vuông C3…Tiếp tục quá trình trên, ta nhận được các dãy các hình vuông C1, C2, C3, …, Cn

Hướng dẫn giải

Số hạng thứ n của cấp số nhân được tính bằng công thức $u_n=u_1.q^{n-1}$ $u_n=u_1.q^{n-1}$trong đó n là số nguyên thỏa mãn $n \ge1$ $n \ge1$

Lời giải:

Gọi $a_n$ là độ dài cạnh của hình vuông Cn. Chứng minh dãy số (an) là một cấp số nhân.

Cạnh của hình vuông C1 là: a1 = 4 (giả thiết)

Theo giả thiết cạnh hình vuông chia thành 4 phần bằng nhau nên theo định lí Pi-ta-go (Pythagore), ta có:

- Cạnh hình vuông thứ hai: C2 = a2 = $\sqrt{1^2+3^2}$ $\sqrt{1^2+3^2}$

- Cạnh hình vuông thứ ba:

${{C}_{3}}={{a}_{3}}=\sqrt{{{\left( \frac{{{a}_{2}}}{4} \right)}^{2}}+{{\left( \frac{3{{a}_{2}}}{4} \right)}^{2}}}={{a}_{2}}.\frac{\sqrt{10}}{4}$ ${{C}_{3}}={{a}_{3}}=\sqrt{{{\left( \frac{{{a}_{2}}}{4} \right)}^{2}}+{{\left( \frac{3{{a}_{2}}}{4} \right)}^{2}}}={{a}_{2}}.\frac{\sqrt{10}}{4}$

Tổng quát cạnh ${{C}_{n+1}}$ ${{C}_{n+1}}$ là:

${{C}_{n+1}}={{a}_{n+1}}=\sqrt{{{\left( \frac{{{a}_{n}}}{4} \right)}^{2}}+{{\left( \frac{3{{a}_{n}}}{4} \right)}^{2}}}={{a}_{n}}\frac{\sqrt{10}}{4}$ ${{C}_{n+1}}={{a}_{n+1}}=\sqrt{{{\left( \frac{{{a}_{n}}}{4} \right)}^{2}}+{{\left( \frac{3{{a}_{n}}}{4} \right)}^{2}}}={{a}_{n}}\frac{\sqrt{10}}{4}$, $\forall n \in \mathbb{N}^*$ $\forall n \in \mathbb{N}^*$

Vậy dãy số (an) là cấp số nhân với số hạng đầu u1 = 4, công bội q = $\dfrac{\sqrt{10}}{4}$ $\dfrac{\sqrt{10}}{4}$

------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập Toán 11 bài 4: Cấp số nhân. Hi vọng qua bài viết bạn đọc có thể học tập tốt hơn môn Toán nhé. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Hóa học lớp 10, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi thpt Quốc gia môn Văn, Thi thpt Quốc gia môn Lịch sử, Thi thpt Quốc gia môn Địa lý, Thi thpt Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.

Giải bài tập trang 28, 29 SGK Giải tích 11: Phương trình lượng giác cơ bản
Giải bài tập Toán 11 ôn tập chương 2: Tổ hợp - xác suất
Giải bài tập Toán 11 bài 1: Phương pháp quy nạp toán học
Giải bài tập Toán 11 bài 2: Dãy số
Giải bài tập Toán 11 bài 3: Cấp số cộng

Tải về Chọn file muốn tải về:

Giải bài tập Toán 11 bài 4: Cấp số nhân

198,4 KB

Giải bài tập Toán 11 bài 4: Cấp số nhân .DOC
135 KB
Giải bài tập Toán 11 bài 4: Cấp số nhân .DOC
135 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này! Đóng 79.000 / tháng Mua ngay Đặc quyền các gói Thành viên PRO Phổ biến nhất PRO+ Tải tài liệu Cao cấp 1 Lớp 30 lượt tải tài liệu Xem nội dung bài viết Trải nghiệm Không quảng cáo Làm bài trắc nghiệm không giới hạn Tìm hiểu thêm Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi: BuriBuriBiBi play mo ...

2 7.087 Bài viết đã được lưu Bài trước Mục lục Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất

Xóa Đăng nhập để Gửi

Tham khảo thêm

Giải bài tập Toán 11 chương 1 bài 2: Phép tịnh tiến
Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
Giải bài tập trang 36, 37 SGK Giải tích 11: Một số phương trình lượng giác thường gặp
Giải bài tập trang 17, 18 SGK Giải tích 11: Hàm số lượng giác
Giải bài tập trang 28, 29 SGK Giải tích 11: Phương trình lượng giác cơ bản
Hình học 11 bài 1: Đại cương về đường thẳng và mặt phẳng
Tóm tắt lý thuyết Toán 11 bài 1: Phép biến hình
Giải bài tập trang 46 SGK Giải tích 11: Quy tắc đếm
Giải bài tập Toán 11 bài 4: Cấp số nhân
Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác

Lớp 11
Giải bài tập Toán lớp 11

Giải bài tập Toán lớp 11

Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
Giải bài tập Toán 11 bài 4: Cấp số nhân
Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác
Hình học 11 bài 1: Đại cương về đường thẳng và mặt phẳng
Giải bài tập trang 36, 37 SGK Giải tích 11: Một số phương trình lượng giác thường gặp
Giải bài tập trang 46 SGK Giải tích 11: Quy tắc đếm

Xem thêm

Gợi ý cho bạn

Bài tập cuối tuần Tiếng Việt lớp 4 Kết nối tri thức Tuần 20 Nâng cao
Bộ đề kiểm tra cuối tuần Tiếng Việt lớp 4 Kết nối tri thức Tuần 20
Bài tập tiếng Anh 7 i-Learn Smart World Unit 1
Tổng hợp từ vựng tiếng Anh lớp 9 chương trình mới

Xem thêm

Từ khóa » Bài Tập Cấp Số Nhân Lớp 11

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Giải bài tập Toán 11 Giải tích: Cấp số nhân

Bài 1 trang 103 SGK Đại số 11

Bài 2 trang 103 SGK Đại số 11

Bài 3 trang 103 SGK Đại số 11

Bài 4 trang 104 SGK Đại số 11

Bài 5 trang 104 SGK Đại số 11

Bài 6 trang 104 SGK Đại số 11

Giải bài tập Toán 11 bài 4: Cấp số nhân

Giải bài tập Toán 11 bài 4: Cấp số nhân .DOC

Giải bài tập Toán 11 bài 4: Cấp số nhân .DOC

Có thể bạn quan tâm

Tham khảo thêm

Giải bài tập Toán 11 chương 1 bài 2: Phép tịnh tiến

Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian

Giải bài tập trang 36, 37 SGK Giải tích 11: Một số phương trình lượng giác thường gặp

Giải bài tập trang 17, 18 SGK Giải tích 11: Hàm số lượng giác

Giải bài tập trang 28, 29 SGK Giải tích 11: Phương trình lượng giác cơ bản

Hình học 11 bài 1: Đại cương về đường thẳng và mặt phẳng

Tóm tắt lý thuyết Toán 11 bài 1: Phép biến hình

Giải bài tập trang 46 SGK Giải tích 11: Quy tắc đếm

Giải bài tập Toán 11 bài 4: Cấp số nhân

Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác

Lớp 11

Giải bài tập Toán lớp 11

Giải bài tập Toán lớp 11

Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian

Giải bài tập Toán 11 bài 4: Cấp số nhân

Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác

Hình học 11 bài 1: Đại cương về đường thẳng và mặt phẳng

Giải bài tập trang 36, 37 SGK Giải tích 11: Một số phương trình lượng giác thường gặp

Giải bài tập trang 46 SGK Giải tích 11: Quy tắc đếm

Gợi ý cho bạn

Bài tập cuối tuần Tiếng Việt lớp 4 Kết nối tri thức Tuần 20 Nâng cao

Bộ đề kiểm tra cuối tuần Tiếng Việt lớp 4 Kết nối tri thức Tuần 20

Bài tập tiếng Anh 7 i-Learn Smart World Unit 1

Tổng hợp từ vựng tiếng Anh lớp 9 chương trình mới

Liên Hệ