Giải Bài Toán Bằng Cách Lập Phương Trình (tiếp) - Giải Bài Tập SGK ...

Có thể bạn quan tâm

- - Mầm non
  - Lớp 1
  - Lớp 2
  - Lớp 3
  - Lớp 4
  - Lớp 5
  - Lớp 6
  - Lớp 7
  - Lớp 8
  - Lớp 9
  - Lớp 10
  - Lớp 11
  - Lớp 12
  - Thi vào lớp 6
  - Thi vào lớp 10
  - Thi Tốt Nghiệp THPT
  - Đánh Giá Năng Lực
  - Khóa Học Trực Tuyến
  - Hỏi bài
  - Trắc nghiệm Online
  - Tiếng Anh
  - Thư viện Học liệu
  - Bài tập Cuối tuần
  - Bài tập Hàng ngày
  - Thư viện Đề thi
  - Giáo án - Bài giảng
  - Tất cả danh mục
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 8 Toán 8 Toán 8 Cánh diều Giải Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp) Giải bài tập SGK Toán lớp 8 bài 7 Bài trước Tải về Bài sau Lớp: Lớp 8 Môn: Toán Bộ sách: Cánh diều Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Giải bài tập Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Trả lời câu hỏi Toán 8 tập 2 trang 28
- Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:
- Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:
Giải bài tập Toán 8 tập 2 trang 30
- Bài 37 (trang 30 SGK Toán 8 Tập 2)
- Bài 38 (trang 30 SGK Toán 8 Tập 2)
- Bài 39 (trang 30 SGK Toán 8 Tập 2)
Giải bài tập toán 8 trang 31, 32 tập 2: Luyện tập
- Bài 40 (trang 31 SGK Toán 8 Tập 2)
- Bài 41 (trang 31 SGK Toán 8 Tập 2)
- Bài 42 (trang 31 SGK Toán 8 Tập 2)
- Bài 43 (trang 31 SGK Toán 8 Tập 2)
- Bài 44 (trang 31 SGK Toán 8 Tập 2)
- Bài 45 (trang 31 SGK Toán 8 Tập 2)
- Bài 46 (trang 31, 32 SGK Toán 8 Tập 2)
- Bài 47 (trang 32 SGK Toán 8 Tập 2)
- Bài 48 (trang 32 SGK Toán 8 Tập 2)
- Bài 49 (trang 32 SGK Toán 8 Tập 2)

Giải bài tập SGK Toán lớp 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp) với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.

Giải bài tập SGK Toán lớp 8 bài 4: Phương trình tích
Giải bài tập SGK Toán lớp 8 bài 5: Phương trình chứa ẩn ở mẫu
Giải bài tập SGK Toán lớp 8 bài 6: Giải bài toán bằng cách lập phương trình

Trả lời câu hỏi Toán 8 tập 2 trang 28

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:

Trong Ví dụ trên, hay thử chọn ẩn số theo cách khác: Gọi s (km) là quãng đường từ Hà Nội đến điểm gặp nhau của hai xe. Điền vào bảng sau rồi lập phương trình với ẩn số s:

	Vận tốc (km/h)	Quãng đường đi (km)	Thời gian đi (h)
Xe máy		s
Ô tô

Lời giải

	Vận tốc (km/h)	Quãng đường đi (km)	Thời gian đi (h)
Xe máy	35	s	$\frac{s}{35}$ $\frac{s}{35}$
Ô tô	45	90 – s	$\frac{90-s}{45}$ $\frac{90-s}{45}$

Ô tô xuất phát sau xe máy 2/5 giờ nên

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:

Giải phương trình nhận được rồi suy ra đáp số của bài toán. So sánh hai cách chọn ẩn, em thấy cách nào cho lời giải gọn hơn?

Lời giải

⇔ 9s = 7(90 - s) + 126

⇔ 9s = 756 - 7s

⇔ 16s = 756

⇔ s = 47,25(km)

Thời gian để hai xe gặp nhau từ lúc xe máy khởi hành là:

Giải bài tập Toán 8 tập 2 trang 30

Bài 37 (trang 30 SGK Toán 8 Tập 2)

Lúc 6 giờ sáng, một xe máy khởi hành từ A để đến B. Sau đó 1 giờ, một ô tô cũng xuất phát từ A đến B với vận tốc trung bình lớn hơn vận tốc trung bình của xe máy 20km/h. Cả hai xe đến B đồng thời vào lúc 9 giờ 30 phút sáng cùng ngày. Tính độ dài quãng đường AB và vận tốc trung bình của xe máy.

Hướng dẫn giải:

Gọi x (km) là quãng đường AB (x > 0).

Thời gian chuyển động từ A đến B của xe máy:

9 giờ 30 phút - 6 giờ = 3 giờ 30 phút $= \dfrac{7}{2}$ $= \dfrac{7}{2}$ (giờ)

Vận tốc của xe máy là: $x : \dfrac{7}{2} = \dfrac{2x}{7}$ $x : \dfrac{7}{2} = \dfrac{2x}{7}$ (km/h)

Ô tô xuất phát sau xe máy 1 giờ và đến B cùng lúc với xe máy 9 giờ 30 phút nên thời gian chuyển động từ A đến B của ô tô là: $\dfrac{7}{2}- 1 = \dfrac{5}{2}$ $\dfrac{7}{2}- 1 = \dfrac{5}{2}$ (giờ)

Vận tốc của ô tô là: $x : \dfrac{5}{2} = \dfrac{2x}{5}$ $x : \dfrac{5}{2} = \dfrac{2x}{5}$ (km/h)

Vì vận tốc của ô tô hơn xe máy 20km/h nên ta có phương trình:

$\dfrac{2x}{5} - \dfrac{2x}{7} = 20$ $\dfrac{2x}{5} - \dfrac{2x}{7} = 20$

$\Leftrightarrow \dfrac{{7.2x}}{{35}} - \dfrac{{5.2x}}{{35}} = \dfrac{{20.35}}{{35}}$ $\Leftrightarrow \dfrac{{7.2x}}{{35}} - \dfrac{{5.2x}}{{35}} = \dfrac{{20.35}}{{35}}$

⇔ 14x - 10x = 700

⇔ 4x = 700

$\Leftrightarrow x=700:4$ $\Leftrightarrow x=700:4$

⇔ x = 175 (thỏa mãn)

Vậy quãng đường AB dài 175 km.

Vận tốc trung bình của xe máy: $175 : \dfrac{7}{2} = 50$ $175 : \dfrac{7}{2} = 50$ (km/h).

Bài 38 (trang 30 SGK Toán 8 Tập 2)

Điểm kiểm tra Toán của một tổ học tập được cho trong bảng sau:

Điểm số (x)	4	5	7	8	9
Tần số (n)	1	*	2	3	*	N=10

Biết điểm trung bình của cả tổ là 6,6. Hãy điền các giá trị thích hợp vào hai ô còn trống (được đánh dấu *).

Hướng dẫn giải:

Gọi x là số học sinh (tần số) được điểm 5(0 < x < 10; x nguyên)

Tần số của điểm 9 là: 10 - (1 + 2 + 3 + x) = 4 - x

Điểm trung bình của cả tổ bằng 6,6 nên ta có phương trình:

$\dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}}= 6,6$ $\dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}}= 6,6$

$\Leftrightarrow \dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}} = \dfrac{{10.6,6}}{{10}}$ $\Leftrightarrow \dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}} = \dfrac{{10.6,6}}{{10}}$

⇔ 4 + 5x + 14 + 24 + 36 - 9x = 66

⇔ -4x + 78 = 66

⇔ - 4x = 66 - 78

⇔ -4x = -12

$\Leftrightarrow x = \left( { - 12} \right):\left( { - 4} \right)$ $\Leftrightarrow x = \left( { - 12} \right):\left( { - 4} \right)$

⇔ x = 3 (thỏa mãn điều kiện)

Tần số của 9 là: 4-x=4-3=1

Vậy tần số của điểm 5 là 3 và tần số của điểm 9 là 1.

Ta điền như sau:

Điểm số (x)	4	5	7	8	9
Tần số (n)	1	3	2	3	1	N=10

Bài 39 (trang 30 SGK Toán 8 Tập 2)

Lan mua hai loại hàng và phải trả tổng cộng 120 nghìn đồng, trong đó đã tính cả 10 nghìn đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với loại hàng thứ nhất là 10%; thuế VAT đối với loại hàng thứ 2 là 8%. Hỏi nếu không kể thuế VAT thì Lan phải trả mỗi loại hàng bao nhiêu tiền?

Ghi chú: Thuế VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Gỉa sử thuế VAT đối với mặt hàng A được quy định là 10%. Khi đó nếu giá bán của A là a đồng thì kể cả thuế VAT, người mua mặt hàng này phải trả tổng cộng là a + 10% a đồng.

Hướng dẫn giải:

Gọi giá gốc của mặt hàng thứ nhất là x (0 < x < 110000 đồng).

Vì trong 120000 đồng Lan trả đã có 10000 đồng thuế VAT nên tổng giá gốc của cả hai mặt hàng chỉ bằng: 120000 – 10000 = 110000 (nghìn đồng).

⇒ Giá gốc của mặt hàng thứ hai là: 110000 – x ( đồng).

Thuế VAT của mặt hàng thứ nhất bằng: 10%.x = 0,1x (đồng).

Thuế VAT của mặt hàng thứ hai bằng: 8%.(110000 – x) = 0,08.(110000 – x) (đồng).

Thuế VAT của cả hai mặt hàng bằng: 0,1x + 0,08(110000 – x) (nghìn đồng).

Theo đề bài, tổng thuế VAT của cả hai mặt hàng là 10000 đồng nên ta có phương trình:

0,1x + 0,08(110000 – x) = 10000

⇔ 0,1x + 8800 – 0,08x = 10000

⇔ 0,02x = 1200

⇔ x = 60000 (thỏa mãn điều kiện).

Vậy không kể VAT thì giá của mặt hàng thứ nhất là 60000 đồng, giá của mặt hàng thứ hai là 110000 – 60000 = 50000 đồng.

Giải bài tập toán 8 trang 31, 32 tập 2: Luyện tập

Bài 40 (trang 31 SGK Toán 8 Tập 2)

Năm nay, tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương thôi. Hỏi năm nay Phương bao nhiêu tuổi?

Hướng dẫn giải:

Gọi x là tuổi Phương năm nay (x > 0; x ∈ N )

Tuổi của mẹ năm nay là: 3x

Tuổi Phương 13 năm sau: x + 13

Tuổi của mẹ 13 năm sau: 3x + 13

13 năm nữa tuổi mẹ chỉ gấp 2 lần tuổi Phương nên ta có phương trình:

3x + 13 = 2(x + 13)

⇔ 3x + 13 = 2x + 26

⇔ 3x – 2x = 26 – 13

⇔ x = 13 (thỏa mãn điều kiện xác định)

Vậy năm nay Phương 13 tuổi.

Bài 41 (trang 31 SGK Toán 8 Tập 2)

Một số tự nhiên có hai chữ số. Chữ số hàng đơn vị gấp hai lần chữ số hàng chục. Nếu thêm chữ số 1 xen vào giữa hai chữ số ấy thì được một số mới lớn hơn số ban đầu 370. Tìm số ban đầu.

Hướng dẫn giải:

Gọi x là chữ số hàng chục $(0 < x \le 9;x \in N)$ $(0 < x \le 9;x \in N)$

Vì chữ số hàng đơn vị gấp hai lần chữ số hàng chục nên chữ số hàng đơn vị là: 2x

Số tự nhiên lúc đầu là: $\overline {x\left( {2x} \right)}$ $\overline {x\left( {2x} \right)}$

Số tự nhiên lúc sau là: $\overline {x1\left( {2x} \right)}$ $\overline {x1\left( {2x} \right)}$

Vì số mới hơn số ban đầu là 370 đơn vị nên ta có phương trình:

$\overline {x1\left( {2x} \right)} - \overline {x\left( {2x} \right)}=370$ $\overline {x1\left( {2x} \right)} - \overline {x\left( {2x} \right)}=370$

⇔ $\left( {100x + 10 + 2x} \right) - \left( {10x + 2x} \right) = 37$ $\left( {100x + 10 + 2x} \right) - \left( {10x + 2x} \right) = 37$

⇔ 100x + 10 + 2x - 10x - 2x = 370

⇔ 90x = 360

⇔ $x=360:90$

⇔x = 4 (thỏa mãn)

Vậy chữ số hàng chục là 4 nên chữ số hàng đơn vị là: 2.4 = 8.

Do đó, số ban đầu là: 48.

* Lưu ý: Vì chỉ có 4 số có hai chữ số thỏa mãn điều kiện chữ số hàng đơn vị gấp đôi chữ số hàng chục là: 12 ; 24 ; 36 ; 48 nên ta có thể đi thử trực tiếp mà không cần giải bằng cách lập phương trình.

Bài 42 (trang 31 SGK Toán 8 Tập 2)

Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm một chữ số 2 vào bên trái và một chữ số 2 vào bên phải số đó thì ta được một số lớn hơn gấp 153 lần số ban đầu.

Hướng dẫn giải:

Gọi số ban đầu là $x(10 \le x \le 99; x ∈\mathbb N)$ $x(10 \le x \le 99; x ∈\mathbb N)$

Nếu viết thêm một chữ số 2 vào bên trái và một chữ số 2 vào bên phải số đó thì ta được số mới là $\overline {2x2}$ $\overline {2x2}$

Vì x là số có hai chữ số nên $\overline {2x2}$ $\overline {2x2}$ là số có bốn chữ số do đó ta có thể tách như sau:

$\overline {2x2}= 2000 + 10x + 2$ $\overline {2x2}= 2000 + 10x + 2$

Vì số mới lớn gấp 153 lần số ban đầu nên ta có phương trình :

$\overline {2x2} = 153x$ $\overline {2x2} = 153x$

$\Leftrightarrow 2000 + 10x + 2 = 153x$ $\Leftrightarrow 2000 + 10x + 2 = 153x$

$\Leftrightarrow 2000 + 2 = 153x - 10x$ $\Leftrightarrow 2000 + 2 = 153x - 10x$

⇔2002 = 143x

$\Leftrightarrow x=2002:143$ $\Leftrightarrow x=2002:143$

⇔ x=14 (thỏa mãn điều kiện)

Vậy số tự nhiên cần tìm là: 14.

Bài 43 (trang 31 SGK Toán 8 Tập 2)

Tìm phân số có đồng thời các tính chất sau:

a) Tử số của phân số là số tự nhiên có một chữ số;

b) Hiệu giữa tử số và mẫu số bằng x - 4;(x ≠ 4).

c) Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số, thì ta được một phân số bằng phân số $\frac{1}{5}$ $\frac{1}{5}$

Hướng dẫn giải:

Gọi x là tử số của phân số cần tìm $(0 < x \le 9); x ∈\mathbb N$ $(0 < x \le 9); x ∈\mathbb N$

Vì hiệu giữa tử số và mẫu số bằng 4 nên tử số lớn hơn mẫu số 4 đơn vị. Suy ra mẫu số của phân số đó là: $x - 4\left( {x \ne 4} \right)$ $x - 4\left( {x \ne 4} \right)$

Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số thì mẫu số mới là: $\overline {\left( {x - 4} \right)x}$ $\overline {\left( {x - 4} \right)x}$

Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số, thì ta được một phân số bằng phân số $\dfrac{1}{5}$ $\dfrac{1}{5}$ nên ta có phương trình:

$\dfrac{x}{{\overline {\left( {x - 4} \right)x} }} = \dfrac{1}{5}$ $\dfrac{x}{{\overline {\left( {x - 4} \right)x} }} = \dfrac{1}{5}$

$\Leftrightarrow \dfrac{{5x}}{{5.\overline {\left( {x - 4} \right)x} }} = \dfrac{{\overline {\left( {x - 4} \right)x} }}{{5.\overline {\left( {x - 4} \right)x} }}$ $\Leftrightarrow \dfrac{{5x}}{{5.\overline {\left( {x - 4} \right)x} }} = \dfrac{{\overline {\left( {x - 4} \right)x} }}{{5.\overline {\left( {x - 4} \right)x} }}$

$\Rightarrow 5x = {\overline {\left( {x - 4} \right)x}}$ $\Rightarrow 5x = {\overline {\left( {x - 4} \right)x}}$

$⇔ 5x = 10\left( {x - 4} \right) + x$ $⇔ 5x = 10\left( {x - 4} \right) + x$

$⇔ 5x = 10x - 40 + x$

$\Leftrightarrow 10x + x - 5x = 40$ $\Leftrightarrow 10x + x - 5x = 40$

$\Leftrightarrow 6x = 40$ $\Leftrightarrow 6x = 40$

$\Leftrightarrow x = 40:6$ $\Leftrightarrow x = 40:6$

$\Leftrightarrow x = \dfrac{{20}}{3}$ $\Leftrightarrow x = \dfrac{{20}}{3}$ (không thỏa mãn).

Vậy không có phân số thỏa mãn các yêu cầu của bài toán.

Bài 44 (trang 31 SGK Toán 8 Tập 2)

Điểm kiểm tra Toán của một lớp được cho trong bảng dưới đây:

Điểm (x)	1	2	3	4	5	6	7	8	9	10
Tần số (f)	0	0	2	*	10	12	7	6	4	1	N = *

trong đó có 2 ô còn trống (thay bằng dấu *). Hãy điền số thích hợp vào ô trống, nếu điểm trung bình của lớp là 6,06.

Hướng dẫn giải:

Gọi x là tần số của điểm 4 (x > 0; x ∈ N)

Số học sinh của lớp:

$\frac{2.3+4.x+5.10+6.12+7.7+6.8+9.4+10.1}{42+x}=6,06$ $\frac{2.3+4.x+5.10+6.12+7.7+6.8+9.4+10.1}{42+x}=6,06$

2 + x + 10 + 12 + 7 + 6 + 4 + 1 = 42 + x

Vì điểm trung bình bằng 6,06 nên:

⇔ 6 + 4x + 50 + 72 + 49 + 48 + 36 + 10 = 6,06(42 + x)

⇔ 271 + 4x = 254,52 + 6,06x ⇔ 16,48 = 2,06x

⇔ x = 8 (thỏa mãn điều kiện đặt ra)

Vậy ta có kết quả điền vào như sau:

Điểm (x)	1	2	3	4	5	6	7	8	9	10
Tần số (f)	0	0	2	8	10	12	7	6	4	1	N = 50

Bài 45 (trang 31 SGK Toán 8 Tập 2)

Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 20 ngày. Do cải tiến kĩ thuật, năng suất dệt của xí nghiệp đã tăng 20%. Bởi vậy, chỉ trong 18 ngày, không những xí nghiệp đã hoàn thành số thảm cần dệt mà còn dệt thêm được 24 tấm nữa. Tính số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng.

Hướng dẫn giải:

Cách 1: Gọi x là năng suất dự tính của xí nghiệp (sản phẩm/ngày); (x ∈ N*) .

⇒ Số thảm len dệt được theo dự tính là: 20x (thảm).

Sau khi cải tiến, năng suất của xí nghiệp đã tăng 20% nên năng suất trên thực tế là: x + 20%.x = x + 0,2x = 1,2x (sản phẩm/ngày).

Sau 18 ngày, xí nghiệp dệt được: 18.1,2x = 21,6.x (thảm).

Vì sau 18 ngày, xí nghiệp không những hoàn thành số thảm cần dệt mà còn dệt thêm được 24 tấm nên ta có phương trình:

21,6.x = 20x + 24

⇔ 21,6x – 20x = 24

⇔ 1,6x = 24

⇔ x = 15 (thỏa mãn)

Vậy số thảm mà xí nghiệp phải dệt ban đầu là: 20.15 = 300 (thảm).

Cách 2:

Gọi x là số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng (x nguyên dương)

Số tấm thảm len mỗi ngày dự định dệt là: $\dfrac{x}{{20}}$ $\dfrac{x}{{20}}$ (tấm)

Số tấm thảm len thực tế đã dệt là: x + 24 (tấm)

Số tấm thảm len thực tế mỗi ngày dệt là: $\dfrac{{x + 24}}{{18}}$ $\dfrac{{x + 24}}{{18}}$ (tấm)

Vì năng suất của xí nghiệp tăng 20% nên số thảm thực tế dệt trong một ngày bằng $100\%+20\%=120\%$ $100\%+20\%=120\%$ số thảm dự định dệt trong một ngày, ta có phương trình:

$\eqalign{ & {{x + 24} \over {18}} = 120\% .{x \over {20}} \cr & \Leftrightarrow {{x + 24} \over {18}} = {6 \over 5}.{x \over {20}} \cr & \Leftrightarrow {{50\left( {x + 24} \right)} \over {900}} = {{9.6x} \over {900}} \cr & \Leftrightarrow 50\left( {x + 24} \right) = 54x \cr & \Leftrightarrow 50x + 1200 = 54x \cr & \Leftrightarrow 1200 = 54x - 50x \cr & \Leftrightarrow 4x = 1200 \cr & \Leftrightarrow x = 1200:4 \cr & \Leftrightarrow x = 300 \text{(thỏa mãn)}\cr}$ $\eqalign{ & {{x + 24} \over {18}} = 120\% .{x \over {20}} \cr & \Leftrightarrow {{x + 24} \over {18}} = {6 \over 5}.{x \over {20}} \cr & \Leftrightarrow {{50\left( {x + 24} \right)} \over {900}} = {{9.6x} \over {900}} \cr & \Leftrightarrow 50\left( {x + 24} \right) = 54x \cr & \Leftrightarrow 50x + 1200 = 54x \cr & \Leftrightarrow 1200 = 54x - 50x \cr & \Leftrightarrow 4x = 1200 \cr & \Leftrightarrow x = 1200:4 \cr & \Leftrightarrow x = 300 \text{(thỏa mãn)}\cr}$

Vậy số tấm thảm len xí nghiệp phải dệt theo hợp đồng là 300 tấm.

Bài 46 (trang 31, 32 SGK Toán 8 Tập 2)

Một người lái ô tô dự định đi từ A đến B với vận tốc 48km/h. Nhưng sau khi đi được 1 giờ với vận tốc ấy, ô tô bị tàu hỏa chắn đường trong 10 phút. Do đó, để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm 6km/h. Tính quãng đường AB.

Hướng dẫn giải:

Gọi x là quãng đường AB (x > 0; km)

Đổi: 10 phút = $\dfrac{1}{6}$ $\dfrac{1}{6}$ giờ.

Đoạn đường ô tô đi trong 1 giờ: 48 km

Đoạn đường còn lại là: x - 48 (km)

Thời gian dự định đi đoạn đường còn lại là: $\dfrac{{x - 48}}{{48}}$ $\dfrac{{x - 48}}{{48}}$ (giờ)

Vận tốc lúc sau là: 48 + 6 = 54 (km/h)

Thời gian thực tế đi đoạn đường còn lại là: $\dfrac{{x - 48}}{{54}}$ $\dfrac{{x - 48}}{{54}}$ (giờ)

Do bị tàu hỏa chắn đường trong 10 phút $=\dfrac{1}{6}$ $=\dfrac{1}{6}$ giờ nên thời gian thực tế ô tô đi đoạn đường còn lại ít hơn dự định là $\dfrac{1}{6}$ $\dfrac{1}{6}$ giờ do đó ta có phương trình:

$\dfrac{{x - 48}}{{48}} - \dfrac{{x - 48}}{{54}} = \dfrac{1}{6}$ $\dfrac{{x - 48}}{{48}} - \dfrac{{x - 48}}{{54}} = \dfrac{1}{6}$

$\Leftrightarrow \dfrac{{9\left( {x - 48} \right)}}{{432}} - \dfrac{{8\left( {x - 48} \right)}}{{432}} = \dfrac{{72}}{{432}}$ $\Leftrightarrow \dfrac{{9\left( {x - 48} \right)}}{{432}} - \dfrac{{8\left( {x - 48} \right)}}{{432}} = \dfrac{{72}}{{432}}$

$⇔9\left( {x - 48} \right) - 8\left( {x - 48} \right) = 72$ $⇔9\left( {x - 48} \right) - 8\left( {x - 48} \right) = 72$

⇔9x - 432 - 8x + 384 = 72

$\Leftrightarrow x - 48 = 72$ $\Leftrightarrow x - 48 = 72$

$\Leftrightarrow x = 72 + 48$ $\Leftrightarrow x = 72 + 48$

⇔x = 120 (thỏa điều kiện đặt ra).

Vậy quãng đường AB dài 120 km.

Bài 47 (trang 32 SGK Toán 8 Tập 2)

Bà An gửi vào quỹ tiết kiệm x nghìn đồng với lãi suất mỗi tháng là a% (a là một số cho trước) và lãi tháng này được tính gộp vào vốn cho tháng sau.

a) Hãy viết biểu thức biểu thị:

+ Số tiền lãi sau tháng thứ nhất;

+ Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất;

+ Tổng số tiền lãi có được sau tháng thứ hai.

b) Nếu lãi suất là 1,2% (tức là a = 1,2) và sau 2 tháng tổng số tiền lãi là 48,288 nghìn đồng, thì lúc đầu bà An đã gửi bao nhiêu tiền tiết kiệm?

Hướng dẫn giải:

a) Bà An gửi vào quỹ tiết kiệm: x đồng (x > 0).

Lãi suất mỗi tháng là a% tháng nên số tiền lãi sau tháng thứ nhất bằng: a%.x

Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất: x + a%.x = (1 + a%)x

Số tiền lãi sau tháng thứ hai: (1 + a%)x.a%

Tổng số tiền lãi sau hai tháng bằng: a%.x + (1 + a%).x.a% (đồng) (1)

b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% (tức là a = 1,2) nên thay vào (1) ta có phương trình:

1,2%.x + (1 + 1,2%).x.1,2% = 48288

⇔ 0,012x + 1,012.x.0,012 = 48288

⇔ 0,012x + 0,012144x = 48288

⇔ 0,024144.x = 48288

⇔ x = 2 000 000 (đồng).

Vậy bà An đã gửi tiết kiệm 2 000 000 đồng.

Bài 48 (trang 32 SGK Toán 8 Tập 2)

Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807200 người. Tính số dân năm ngoái của mỗi tỉnh.

Hướng dẫn giải:

Gọi x là số dân năm ngoái của tỉnh A (0 < x < 4; x ∈ N*; triệu người)

Số dân năm ngoái của tỉnh B: 4 – x (triệu người).

Năm nay dân số của tỉnh A tăng 1,1 % nên số dân của tỉnh A năm nay: x + 1,1% x = 1,011.x

Năm nay dân số của tỉnh B tăng 1,2 % nên số dân của tỉnh B năm nay: (4 – x) + 1,2% (4 – x) = 1,012(4 – x)

Vì số dân tỉnh A năm nay hơn tỉnh B là 807200 người = 0,8072 triệu người nên ta có phương trình:

1,011.x - 1,012(4 – x) = 0,8072

⇔ 1,011x – 4,048 + 1,012x = 0,8072

⇔ 2,023. x = 4,8552

⇔ x = 2,4 (thỏa mãn).

Vậy dân số của tỉnh A năm ngoái là 2,4 triệu người, dân số tỉnh B năm ngoái là 4 – 2,4 = 1,6 triệu người

Bài 49 (trang 32 SGK Toán 8 Tập 2)

Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từ miếng bìa đó ra một hình chữ nhật có chiều dài 2cm như hình 5 thì hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.

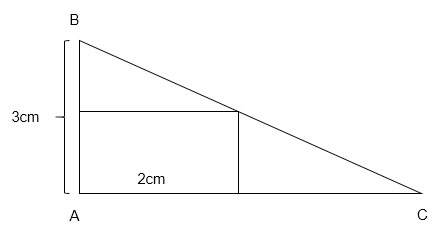
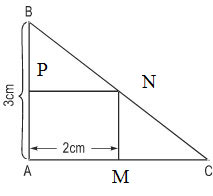
Bài 49

Hướng dẫn giải:

Bài 49

Gọi x (cm) là độ dài cạnh AC (x >2 ).

Gọi hình chữ nhật là MNPA (như hình vẽ) thì MC = x – 2 (cm)

Vì MN // AB nên $\dfrac{{MN}}{{AB}} = \dfrac{{MC}}{{AC}}$ $\dfrac{{MN}}{{AB}} = \dfrac{{MC}}{{AC}}$ (hệ quả của định lí TaLet)

$\Rightarrow MN = \dfrac{{AB.MC}}{{AC}} = \dfrac{{3\left( {x - 2} \right)}}{x}(cm)$ $\Rightarrow MN = \dfrac{{AB.MC}}{{AC}} = \dfrac{{3\left( {x - 2} \right)}}{x}(cm)$

Diện tích hình chữ nhật MNPA là: $2.\dfrac{{3\left( {x - 2} \right)}}{x} = \dfrac{{6\left( {x - 2} \right)}}{x}$ $2.\dfrac{{3\left( {x - 2} \right)}}{x} = \dfrac{{6\left( {x - 2} \right)}}{x}$

Diện tích hình tam giác ABC là: $\dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.x = \dfrac{3}{2}x$ $\dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.x = \dfrac{3}{2}x$

Vì diện tích hình chữ nhật MNPA bằng một nửa diện tích hình tam giác ABC nên ta có phương trình:

$\eqalign{ & {3 \over 2}x = 2.{{6\left( {x - 2} \right)} \over x} \cr & \Leftrightarrow {{3x.x} \over {2x}} = {{2.2.6\left( {x - 2} \right)} \over {2x}} \cr & \Rightarrow 3{x^2} = 24x - 48 \cr & \Leftrightarrow 3{x^2} - 24x + 48 = 0 \cr & \Leftrightarrow {x^2} - 8x + 16 = 0 \cr & \Leftrightarrow {x^2} - 2.x.4 + {4^2} = 0 \cr & \Leftrightarrow {\left( {x - 4} \right)^2} = 0 \cr & \Leftrightarrow x - 4 = 0 \cr & \Leftrightarrow x = 4\text{ (thỏa mãn)} \cr}$ $\eqalign{ & {3 \over 2}x = 2.{{6\left( {x - 2} \right)} \over x} \cr & \Leftrightarrow {{3x.x} \over {2x}} = {{2.2.6\left( {x - 2} \right)} \over {2x}} \cr & \Rightarrow 3{x^2} = 24x - 48 \cr & \Leftrightarrow 3{x^2} - 24x + 48 = 0 \cr & \Leftrightarrow {x^2} - 8x + 16 = 0 \cr & \Leftrightarrow {x^2} - 2.x.4 + {4^2} = 0 \cr & \Leftrightarrow {\left( {x - 4} \right)^2} = 0 \cr & \Leftrightarrow x - 4 = 0 \cr & \Leftrightarrow x = 4\text{ (thỏa mãn)} \cr}$

Vậy AC = 4cm.

........................

Giải Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp) được VnDoc chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, đưa ra các phương pháp định hướng giải bài và làm bài tập cụ thể, thông qua giải bài tập các em nắm chắc kiến thức môn Toán lớp 8.

Ngoài Giải Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp), các bạn có thể tham khảo thêm Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc.

Tải về Chọn file muốn tải về:

Giải Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

562,3 KB

Tải file định dạng .DOC
917,5 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này! Đóng 79.000 / tháng Mua ngay Đặc quyền các gói Thành viên PRO Phổ biến nhất PRO+ Tải tài liệu Cao cấp 1 Lớp 30 lượt tải tài liệu Xem nội dung bài viết Trải nghiệm Không quảng cáo Làm bài trắc nghiệm không giới hạn Tìm hiểu thêm Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi: Đinh Thị Nhàn

18 10.817 Bài viết đã được lưu Bài trước Mục lục Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất

Xóa Đăng nhập để Gửi Tìm bài trong mục này

ĐẠI SỐ - Chương 1: Phép nhân và phép chia các đa thức
- Bài 1: Nhân đơn thức với đa thức
  - Toán 8 Bài 1: Nhân đơn thức với đa thức
  - Giải SBT Toán 8 bài 1 Nhân đơn thức với đa thức
- Bài 2: Nhân đa thức với đa thức
  - Toán 8 Bài 2: Nhân đa thức với đa thức
  - Giải bài tập SBT Toán 8 bài 2: Nhân đa thức với đa thức
- Bài 3: Những hằng đẳng thức đáng nhớ
  - Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ
  - Giải SBT Toán 8 bài 3, 4, 5: Những hằng đẳng thức đáng nhớ
- Bài 4: Những hằng đẳng thức đáng nhớ (tiếp)
  - Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp)
  - Giải SBT Toán 8 bài 3, 4, 5: Những hằng đẳng thức đáng nhớ
- Bài 5: Những hằng đẳng thức đáng nhớ (tiếp)
  - Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo)
  - Giải SBT Toán 8 bài 3, 4, 5: Những hằng đẳng thức đáng nhớ
- Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
  - Toán 8 Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
  - Giải bài tập SBT Toán 8 bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
  - Toán 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
  - Giải bài tập SBT Toán 8 bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
  - Toán 8 Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
  - Giải bài tập SBT Toán 8 bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
  - Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
  - Giải bài tập SBT Toán 8 bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10: Chia đơn thức cho đơn thức
  - Toán 8 Bài 10: Chia đơn thức cho đơn thức
  - Giải bài tập SBT Toán 8 bài 10: Chia đơn thức cho đơn thức
- Bài 11: Chia đa thức cho đơn thức
  - Toán 8 Bài 11: Chia đa thức cho đơn thức
  - Giải bài tập SBT Toán 8 bài 11: Chia đa thức cho đơn thức
- Bài 12: Chia đa thức một biến đã sắp xếp
  - Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp
  - Giải bài tập SBT Toán 8 bài 12: Chia đa thức một biến đã sắp xếp
- Ôn tập chương 1
  - Giải bài tập SGK Toán lớp 8: Ôn tập chương 1
  - Toán 8: Ôn tập chương 1 Đại số
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương 1
ĐẠI SỐ Chương 2: Phân thức đại số
- Bài 1: Phân thức đại số
  - Toán 8 Bài 1 Phân thức đại số
  - Giải bài tập SGK Toán lớp 8 Bài 1: Phân thức đại số
  - Giải bài tập SBT Toán 8 bài 1: Phân thức đại số
- Bài 2: Tính chất cơ bản của phân thức
  - Giải bài tập SGK Toán lớp 8 bài 2: Tính chất cơ bản của phân thức
  - Giải bài tập SBT Toán 8 bài 2: Tính chất cơ bản của phân thức
- Bài 3: Rút gọn phân thức
  - Giải bài tập SBT Toán 8 bài 3: Rút gọn phân thức
  - Giải Toán 8 bài 3: Rút gọn phân thức
- Bài 4: Quy đồng mẫu thức nhiều phân thức
  - Giải bài tập SBT Toán 8 bài 4: Quy đồng mẫu thức nhiều phân thức
  - Giải bài tập SGK Toán lớp 8 bài 4: Quy đồng mẫu thức nhiều phân thức
- Bài 5: Phép cộng các phân thức đại số
  - Giải bài tập SBT Toán 8 bài 5: Phép cộng các phân thức đại số
  - Giải bài tập SGK Toán lớp 8 bài 5: Phép cộng các phân thức đại số
- Bài 6: Phép trừ các phân thức đại số
  - Giải bài tập SBT Toán 8 bài 6: Phép trừ các phân thức đại số
  - Giải bài tập SGK Toán lớp 8 bài 6: Phép trừ các phân thức đại số
- Bài 7: Phép nhân các phân thức đại số
  - Giải bài tập SBT Toán 8 bài 7: Phép nhân các phân thức đại số
  - Giải bài tập SGK Toán lớp 8 bài 7: Phép nhân các phân thức đại số
- Bài 8: Phép chia các phân thức đại số
  - Giải bài tập SBT Toán 8 bài 8: Phép chia các phân thức đại số
  - Giải bài tập SGK Toán lớp 8 bài 8: Phép chia các phân thức đại số
- Bài 9: Biến đổi các biểu thức hữu tỉ - Giá trị của phân thức
  - Giải bài tập SBT Toán 8 bài 9: Biến đổi các biểu thức hữu tỉ - Giá trị của phân thức
  - Giải bài tập SGK Toán lớp 8 bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài: Ôn tập chương 2
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương 2
  - Giải bài tập SGK Toán lớp 8: Ôn tập chương 2
HÌNH HỌC - Chương 1: Tứ giác
- Bài 1: Tứ giác
  - Toán 8 Bài 1: Tứ giác
  - Giải bài tập SBT Toán 8 bài 1: Tứ giác
  - Giải bài tập SGK Toán lớp 8 bài 1: Tứ giác
- Bài 2: Hình thang
  - Toán 8 Bài 2: Hình thang
  - Giải bài tập SBT Toán 8 bài 2: Hình thang
  - Giải bài tập SGK Toán lớp 8 bài 2: Hình thang
- Bài 3: Hình thang cân
  - Toán 8 Bài 3: Hình thang cân
  - Giải bài tập SBT Toán 8 bài 3: Hình thang cân
  - Giải bài tập SGK Toán lớp 8 bài 3: Hình thang cân
- Bài 4: Đường trung bình của tam giác, của hình thang
  - Toán 8 Bài 4: Đường trung bình của tam giác, đường trung bình của hình thang
  - Giải Bài 4: Đường trung bình của tam giác, của hình thang
  - Giải bài tập SBT Toán 8 bài 4: Đường trung bình của tam giác, của hình thang
- Bài 5: Dựng hình bằng thước và compa - Dựng hình thang
  - Giải bài tập SBT Toán 8 bài 5: Dựng hình bằng thước và comp - Dựng hình thang
  - Giải bài tập SGK Toán lớp 8 bài 5: Dựng hình bằng thước và com-pa. Dựng hình thang
- Bài 6: Đối xứng trục
  - Giải bài tập SBT Toán 8 bài 6: Đối xứng trực
  - Giải bài tập SGK Toán lớp 8 bài 6: Đối xứng trục
- Bài 7: Hình bình hành
  - Dấu hiệu nhận biết hình bình hành
  - Giải bài tập SBT Toán 8 bài 7: Hình bình hành
  - Giải bài tập SGK Toán lớp 8 bài 7: Hình bình hành
- Bài 8: Đối xứng tâm
  - Giải bài tập SBT Toán 8 bài 8: Đối xứng tâm
  - Giải bài tập SGK Toán lớp 8 bài 8: Đối xứng tâm
- Bài 9: Hình chữ nhật
  - Giải bài tập SBT Toán 8 bài 9: Hình chữ nhật
  - Giải Toán lớp 8 bài 9: Hình chữ nhật
- Bài 10: Đường thẳng song song với một đường thẳng cho trước
  - Giải bài tập SBT Toán 8 bài 10: Đường thẳng song song với một đường thẳng cho trước
  - Giải bài tập SGK Toán lớp 8 bài 10: Đường thẳng song song với một đường thẳng cho trước
- Bài 11: Hình thoi
  - Giải bài tập SBT Toán 8 bài 11: Hình thoi
  - Giải bài tập SGK Toán lớp 8 bài 11: Hình thoi
- Bài 12: Hình vuông
  - Giải bài tập SBT Toán 8 bài 12: Hình vuông
  - Giải Toán 8 bài 12: Hình vuông
- Bài: Ôn tập chương 1
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương I
  - Giải bài tập SGK Toán lớp 8: Ôn tập chương 1. Tứ giác
HÌNH HỌC - Chương 2: Đa giác - Diện tích đa giác
- Bài 1: Đa giác - Đa giác đều
  - Giải bài tập SBT Toán 8 bài 1: Đa giác - Đa giác đều
  - Giải bài tập SGK Toán lớp 8 bài 1: Đa giác. Đa giác đều
- Bài 2: Diện tích hình chữ nhật
  - Giải bài tập SBT Toán 8 bài 2: Diện tích hình chữ nhật
  - Giải bài tập SGK Toán lớp 8 bài 2: Diện tích hình chữ nhật
- Bài 3: Diện tích tam giác
  - Giải bài tập SBT Toán 8 bài 3: Diện tích tam giác
  - Giải bài tập SGK Toán lớp 8 bài 3: Diện tích tam giác
- Bài 4: Diện tích hình thang
  - Giải bài tập SGK Toán lớp 8 bài 3: Diện tích hình thang
  - Giải bài tập SBT Toán 8 bài 4: Diện tích hình thang
- Bài 5: Diện tích hình thoi
  - Giải bài tập SBT Toán 8 bài 5: Diện tích hình thoi
  - Giải bài tập SGK Toán lớp 8 bài 5: Diện tích hình thoi
  - Công thức tính diện tích hình thoi, chu vi hình thoi
- Bài 6: Diện tích đa giác
  - Giải bài tập SBT Toán 8 bài 6: Diện tích đa giác
  - Giải bài tập SGK Toán lớp 8 bài 6: Diện tích đa giác
- Bài: Ôn tập chương 2
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương II
  - Giải bài tập SGK Toán lớp 8: Ôn tập chương 2 - Đa giác. Điện tích đa giác
Ôn thi học kì 1
ĐẠI SỐ Chương 3: Phương trình bậc nhất một ẩn
- Bài 1: Mở đầu về phương trình
  - Giải bài tập SGK trang 6, 7 Toán 8 tập 2: Mở đầu về phương trình - Luyện tập
  - Giải bài tập SBT Toán 8 bài 1: Mở đầu về phương trình
- Bài 2: Phương trình bậc nhất một ẩn và cách giải
  - Giải bài tập SGK Toán lớp 8 bài 2: Phương trình bậc nhất một ẩn và cách giải
  - Giải bài tập SBT Toán 8 bài 2: Phương trình bậc nhất một ẩn và cách giải
- Bài 3: Phương trình đưa về dạng ax + b = 0
  - Giải bài tập SGK Toán lớp 8 bài 3: Phương trình đưa được về dạng ax + b = 0
  - Giải bài tập SBT Toán 8 bài 3: Phương trình đưa về dạng ax + b = 0
- Bài 4: Phương trình tích
  - Giải bài tập SGK Toán lớp 8 bài 4: Phương trình tích
  - Giải bài tập SBT Toán 8 bài 4: Phương trình tích
- Bài 5: Phương trình chứa ẩn ở mẫu
  - Giải bài tập SGK Toán lớp 8 bài 5: Phương trình chứa ẩn ở mẫu
  - Giải bài tập SBT Toán 8 bài 5: Phương trình chứa ẩn ở mẫu
- Bài 6 - 7: Giải bài toán bằng cách lập phương trình
  - Giải bài tập SGK Toán lớp 8 bài 6: Giải bài toán bằng cách lập phương trình
  - Giải bài tập SGK Toán lớp 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp)
  - Giải bài tập SBT Toán 8 bài 6-7: Giải bài toán bằng cách lập phương trình
- Bài: Ôn tập chương 3
  - Giải bài tập SGK Toán lớp 8 bài: Ôn tập chương III: Phương trình bậc nhất một ẩn
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương 3
- Ôn thi giữa kì 2
ĐẠI SỐ Chương 4: Bất phương trình bậc nhất một ẩn
- Bài 1: Liên hệ giữa thứ tự và phép cộng
  - Giải bài tập SGK Toán lớp 8 bài 1: Liên hệ giữa thứ tự và phép cộng
  - Giải bài tập SBT Toán 8 bài 1: Liên hệ giữa thứ tự và phép cộng
- Bài 2: Liên hệ giữa thứ tự và phép nhân
  - Giải bài tập SGK Toán lớp 8 bài 2: Liên hệ giữa thứ tự và phép nhân
  - Giải bài tập SBT Toán 8 bài 2: Liên hệ giữa thứ tự và phép nhân
- Bài 3: Bất phương trình một ẩn
  - Giải bài tập SGK Toán lớp 8 bài 3: Bất phương trình một ẩn
  - Giải bài tập SBT Toán 8 bài 3: Bất phương trình một ẩn
- Bài 4: Bất phương trình bạc nhất một ẩn
  - Giải bài tập SGK Toán lớp 8 bài 4: Bất phương trình bậc nhất một ẩn
  - Giải bài tập SBT Toán 8 bài 4: Bất phương trình bạc nhất một ẩn
- Bài 5: Phương trình chứa dấu giá trị tuyệt đối
  - Giải bài tập SGK Toán lớp 8 bài 5: Phương trình chứa dấu giá trị tuyệt đối
  - Giải bài tập SBT Toán 8 bài 5: Phương trình chứa dấu giá trị tuyệt đối
- Bài: Ôn tập chương 4
  - Giải bài tập SGK Toán lớp 8 bài: Ôn tập chương IV- Bất phương trình bậc nhất một ẩn
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương 4
HÌNH HỌC - Chương 3: Tam giác đồng dạng
- Bài 1: Định lí Ta-lét trong tam giác
  - Giải bài tập SGK Toán lớp 8 bài 1: Định lí Ta-lét trong tam giác
  - Giải bài tập SBT Toán 8 bài 1: Định lí Ta-lét trong tam giác
- Bài 2: Định lí đảo và hệ quả của định lí Ta-lét
  - Giải bài tập SGK Toán lớp 8 bài 2: Định lí đảo và hệ quả của định lí Ta-lét
  - Giải bài tập SBT Toán 8 bài 2: Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3: Tính chất đường phân giác của tam giác
  - Giải bài tập SGK Toán lớp 8 bài 3: Tính chất đường phân giác của tam giác
  - Giải bài tập SBT Toán 8 bài 3: Tính chất đường phân giác của tam giác
- Bài 4: Khái niệm hai tam giác đồng dạng
  - Giải bài tập trang 71, 72 SGK Toán lớp 8 tập 2: Hai tam giác đồng dạng
  - Giải bài tập SBT Toán 8 bài 4: Khái niệm hai tam giác đồng dạng
- Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)
  - Giải bài tập SGK Toán lớp 8 bài 5: Trường hợp đồng dạng thứ nhất
  - Giải bài tập SBT Toán 8 bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)
  - Giải bài tập SGK Toán lớp 8 bài 6: Trường hợp đồng dạng thứ hai
  - Giải bài tập SBT Toán 8 bài 6: Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7: Trường hợp đồng dạng thứ ba (g.g)
  - Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba
  - Giải bài tập SBT Toán 8 bài 7: Trường hợp đồng dạng thứ ba (g.g)
- Bài 8: Các trường hợp đồng dạng của tam giác vuông
  - Giải bài tập SGK Toán lớp 8 bài 8: Các trường hợp đồng dạng của tam giác vuông
  - Giải bài tập SBT Toán 8 bài 8: Các trường hợp đồng dạng của tam giác vuông
- Bài: Ôn tập chương 3
  - Giải bài tập SGK Toán lớp 8 bài: Ôn tập chương III - Tam giác đồng dạng
  - Giải bài tập SBT Toán 8 bài: Ôn tập chương III
HÌNH HỌC - Chương 4: Hình lăng trụ đứng - Hình chóp đều
- A - Hình lăng trụ đứng
  - Bài 1: Hình hộp chữ nhật
    - Giải bài tập SGK Toán lớp 8 bài 1: Hình hộp chữ nhật
    - Giải bài tập SBT Toán 8 bài 1: Hình hộp chữ nhật
  - Bài 2: Hình hộp chữ nhật (tiếp)
    - Giải bài tập SGK Toán lớp 8 bài 2: Hình hộp chữ nhật (tiếp)
    - Giải bài tập SBT Toán 8 bài 2: Hình hộp chữ nhật
  - Bài 3: Thể tích của hình hộp chữ nhật
    - Giải bài tập SGK Toán lớp 8 bài 3: Thể tích của hình hộp chữ nhật
    - Giải bài tập SBT Toán 8 bài 3: Thể tích của hình hộp chữ nhật
  - Bài 4: Hình lăng trụ đứng
    - Giải bài tập SGK Toán lớp 8 bài 4: Hình lăng trụ đứng
    - Giải bài tập SBT Toán 8 bài 4: Hình lăng trụ đứng
  - Bài 5: Diện tích xung quanh của hình lăng trụ đứng
    - Giải bài tập SGK Toán lớp 8 bài 5: Diện tích xung quanh của hình lăng trụ đứng
    - Giải bài tập SBT Toán 8 bài 5: Diện tích xung quanh của hình lăng trụ đứng
  - Bài 6: Thể tích của hình lăng trụ đứng
    - Giải bài tập SGK Toán lớp 8 bài 6: Thể tích của hình lăng trụ đứng
    - Giải bài tập SBT Toán 8 bài 6: Thể tích của hình lăng trụ đứng
- B - Hình chóp đều
  - Bài 7: Hình chóp đều và hình chóp cụt đều
    - Giải bài tập SGK Toán lớp 8 bài 7: Hình chóp đều và hình chóp cụt đều
    - Giải bài tập SBT Toán 8 bài 7: Hình chóp đều và hình chóp cụt đều
  - Bài 8: Diện tích xung quanh của hình chóp đều
    - Giải bài tập SGK Toán lớp 8 bài 8: Diện tích xung quanh của hình chóp đều
    - Giải bài tập SBT Toán 8 bài 8: Diện tích xung quanh của hình chóp đều
  - Bài 9: Thể tích của hình chóp đều
  - Hình chóp đều: Hình chóp đều tam giác, hình chóp đều tứ giác
  - Giải bài tập SGK Toán lớp 8 bài 9: Thể tích của hình chóp đều
  - Ôn tập chương 4
  - Giải bài tập SGK Toán lớp 8 bài: Ôn tập chương IV - Hình lăng trụ đứng. Hình chóp đều
Ôn thi học kì 2

Lớp 8
Toán 8
Toán 8 Cánh diều
Đề thi giữa kì 1 lớp 8
Đề thi học kì 1 lớp 8
Đề thi giữa kì 2 lớp 8
Đề thi học kì 2 lớp 8
Đề kiểm tra 15 phút lớp 8
Thi học sinh giỏi lớp 8
Toán 8 Kết nối tri thức
Toán 8 Chân trời sáng tạo
Giải Bài Tập Toán 8
Lý thuyết Toán 8
Soạn Toán 8 VNEN
Bài tập Toán 8

Tham khảo thêm

Giải Toán 8 bài 5: Diện tích hình thoi
Giải Toán 8 bài 2: Phương trình bậc nhất một ẩn và cách giải
Toán 8 Cánh diều bài 1 trang 94, 95, 96, 97
Giải Toán 8 bài 3: Phương trình đưa được về dạng ax + b = 0
Toán 8 Cánh diều bài 4 trang 24, 25, 26, 27
Giải Toán 8 bài 1 Sách mới
Toán 8 Cánh diều bài 1: Phân thức đại số
Giải bài tập SGK Toán lớp 8 bài 6: Diện tích đa giác
Giải bài tập SGK Toán lớp 8: Ôn tập chương 2 - Đa giác. Diện tích đa giác
Giải bài tập SGK Toán lớp 8 bài 3: Diện tích tam giác

Toán 8 Cánh diều

Toán 8 Cánh diều Bài tập cuối chương I
Giải Toán 8 bài 1 Sách mới
Toán 8 Cánh diều bài 1: Phân thức đại số
Toán 8 Cánh diều bài 1 trang 94, 95, 96, 97
Toán 8 Cánh diều bài 3 trang 18, 19, 20, 21, 22, 23
Toán 8 Cánh diều bài 4 trang 24, 25, 26, 27

Xem thêm

Gợi ý cho bạn

TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4
Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao
Được 18-20 điểm khối A1 nên đăng ký trường nào?
Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1

Xem thêm

Từ khóa » Toán 8 Bài 7 Giải Toán Bằng Cách Lập Phương Trình

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Giải bài tập Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Trả lời câu hỏi Toán 8 tập 2 trang 28

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:

Giải bài tập Toán 8 tập 2 trang 30

Bài 37 (trang 30 SGK Toán 8 Tập 2)

Bài 38 (trang 30 SGK Toán 8 Tập 2)

Bài 39 (trang 30 SGK Toán 8 Tập 2)

Giải bài tập toán 8 trang 31, 32 tập 2: Luyện tập

Bài 40 (trang 31 SGK Toán 8 Tập 2)

Bài 41 (trang 31 SGK Toán 8 Tập 2)

Bài 42 (trang 31 SGK Toán 8 Tập 2)

Bài 43 (trang 31 SGK Toán 8 Tập 2)

Bài 44 (trang 31 SGK Toán 8 Tập 2)

Bài 45 (trang 31 SGK Toán 8 Tập 2)

Bài 46 (trang 31, 32 SGK Toán 8 Tập 2)

Bài 47 (trang 32 SGK Toán 8 Tập 2)

Bài 48 (trang 32 SGK Toán 8 Tập 2)

Bài 49 (trang 32 SGK Toán 8 Tập 2)

Giải Toán 8 bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Tải file định dạng .DOC

Có thể bạn quan tâm

ĐẠI SỐ - Chương 1: Phép nhân và phép chia các đa thức

ĐẠI SỐ Chương 2: Phân thức đại số

HÌNH HỌC - Chương 1: Tứ giác

HÌNH HỌC - Chương 2: Đa giác - Diện tích đa giác

Ôn thi học kì 1

ĐẠI SỐ Chương 3: Phương trình bậc nhất một ẩn

ĐẠI SỐ Chương 4: Bất phương trình bậc nhất một ẩn

HÌNH HỌC - Chương 3: Tam giác đồng dạng

HÌNH HỌC - Chương 4: Hình lăng trụ đứng - Hình chóp đều

Ôn thi học kì 2

Lớp 8

Toán 8

Toán 8 Cánh diều

Đề thi giữa kì 1 lớp 8

Đề thi học kì 1 lớp 8

Đề thi giữa kì 2 lớp 8

Đề thi học kì 2 lớp 8

Đề kiểm tra 15 phút lớp 8

Thi học sinh giỏi lớp 8

Toán 8 Kết nối tri thức

Toán 8 Chân trời sáng tạo

Giải Bài Tập Toán 8

Lý thuyết Toán 8

Soạn Toán 8 VNEN

Bài tập Toán 8

Tham khảo thêm

Giải Toán 8 bài 5: Diện tích hình thoi

Giải Toán 8 bài 2: Phương trình bậc nhất một ẩn và cách giải

Toán 8 Cánh diều bài 1 trang 94, 95, 96, 97

Giải Toán 8 bài 3: Phương trình đưa được về dạng ax + b = 0