Giải Bài Toán Cực Trị Số Phức Bằng Phương Pháp Hình ...

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

• Tất cả
  • Học tập
  • Tài liệu
  • Hướng dẫn
• • Học tập
  • Tài liệu
  • Hướng dẫn
  • Đề thi
  • Học tiếng Anh
  • Giáo án
  • Bài giảng điện tử
  • Tài liệu Giáo viên
  • Tập huấn Giáo viên

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Download.vn Học tập Lớp 12 Toán 12 Giải bài toán cực trị số phức bằng phương pháp hình học giải tích Giải số phức bằng hình học giải tích Tải về Bình luận

• 1

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo

Tìm hiểu thêm » Mua Pro 79.000đ Hỗ trợ qua Zalo

Giải bài toán cực trị số phức bằng phương pháp hình học giải tích là tài liệu hướng dẫn giải bài toán cực trị số phức bằng phương pháp hình học giải tích. Đây là lớp các bài toán vận dụng cao số phức và thường xuất hiện trong đề thi THPT Quốc gia.

Hy vọng với tài liệu này các bạn học sinh lớp 12 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt kết quả cao trong các bài kiểm tra, bài thi học kì và thi THPT Quốc gia đạt kết quả cao. Đồng thời đây cũng là tài liệu hữu ích giúp quý thầy cô có thêm nhiều tư liệu trong giảng dạy. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.

Hướng dẫn giải bài tập số phức bằng hình học giải tích

Trang 1 MỞ ĐẦU Trong chương trình Toán THPT, phần Đại số mà cụ thể là phần Số học, ở chương trình lớp 12, học sinh được hoàn thiện hiểu biết của mình về các tập hợp số thông qua việc cung cấp một tập hợp số, gọi là Số phức. Trong chương này, học sinh đã bước đầu làm quen với các phép toán cộng, trừ, nhân, chia, khai căn, lũy thừa; lấy mô đun, …các số phức. Bằng cách đặt tương ứng mỗi số phức 2,(;,1)zxyixyi với mỗi điểm (;)Mxy trên mặt phẳng tọa độ Oxy, ta thấy giữa Đại số và Hình học có mối liên hệ với nhau khá “gần gũi”. Hơn nữa, nhiều bài toán Đại số bên Số phức, khi chuyển sang Hình học, từ những con số khá trừu tượng, bài toán đã được minh họa một cách rất trực quan, sinh động và cũng giải được bằng Hình học với phương pháp rất đẹp. Đặc biệt, trong các kỳ thi Đại học, Cao đẳng và THPT Quốc gia những năm gần đây, việc sử dụng phương pháp Hình học để giải quyết các bài toán về Số phức là một trong những phương pháp khá hay và hiệu quả, đặc biệt là các bài toán về Cực trị trong số phức. Hơn nữa, với những bài toán Hình học theo phương pháp trắc nghiệm, nếu khi biểu diễn được trên giấy thì qua hình ảnh minh họa, ta có thể lựa chọn đáp án một cách dễ dàng. Tuy nhiên, trong thực tế giảng dạy, việc chuyển từ bài toán Đại số nói chung và Số phức nói riêng sang bài toán Hình học ở nhiều học sinh nói chung còn khá nhiều lúng túng, vì vậy việc giải các bài toán về Số phức gây ra khá nhiều khó khăn cho học sinh. Bài toán Cực trị Số phức thông thường thì có khá nhiều cách lựa chọn để giải như dùng Bất đẳng thức, dùng Khảo sát hàm số, … Qua chuyên đề này, tôi muốn gợi ý cho học sinh một lối tư duy vận dụng linh hoạt các phương pháp chuyển đổi từ bài toán Đại số sang Hình học cho học sinh, giúp các em có cái nhìn cụ thể hơn về việc chuyển đổi đó và vận duy tư duy này cho những bài toán khác. Với mục tiêu đó, trong chuyên đề này, tôi chỉ tập trung giải quyết bài toán theo hướng Hình học. Không đặt nặng việc so sánh phương pháp nào nhanh hơn, tối ưu hơn phương pháp nào. Trang 2 II. NỘI DUNG 1. Một số kiến thức, kí hiệu ban đầu 1.1 Các định nghĩa và kí hiệu a) Số i:Ta thừa nhận có một số mà bình phương của nó bằng 1. Kí hiệu: .i Như vậy, 21.i b) Số phức: Cho ,,xy biểu thức zxyi gọi là một (dạng đại số) số phức. :x Phần thực; :y Phần ảo c) Với mỗi số phức ,zxyi giá trị biểu thức 22xy gọi là mô đun của .z Kí hiệu: z. Như vậy, 22.zxy d) Với mỗi số phức .zxyi Số phức '()zxyixyi  gọi là số phức liên hợp của số phức .z Kí hiệu z. Như vậy, zxyi thì .zxyi e) Với mỗi số phức .zxyi Xác định điểm (;)Mxy trên mặt phẳng tọa độ Oxy. Điểm M gọi là biểu diễn hình học của số phức .z Để cho tiện, trong tập tài liệu này, tôi kí hiệu (;)()MxyMz hay đơn giản ()Mz để chỉ M là điểm biểu diễn cho số phức .zxyi 1.2 Các phép toán trên tập hợp số phức Cho hai số phức 2,'''.(,,',',1)zxyizxyixyxyi + Phép cộng: '(')(')zzxxyyi + Phép trừ: '(')(')zzxxyyi + Phép nhân: .'('')('')zzxxyyxyxyi + Phép chia: .'''.'zz zzzz với '00 .zi 1.3 Một số kí hiệu chuyển từ số phức sang tọa độ Oxy quen thuộc. + Với ()Mz thì .zOM + Với (),''(')MMzMMz thì ''.zzMM + Với (),(),ABAAzBBz trong đó ,ABzz là hai số phức khác nhau cho trước thì tập hợp các điểm ()MMz thỏa mãn hệ thức ABzzzz là đường trung trực của đoạn .AB + Với 000(),R0MMz, tập hợp các điểm ()MMz thỏa mãn hệ thức 0Rzz là đường tròn tâm 0,M bán kính R. 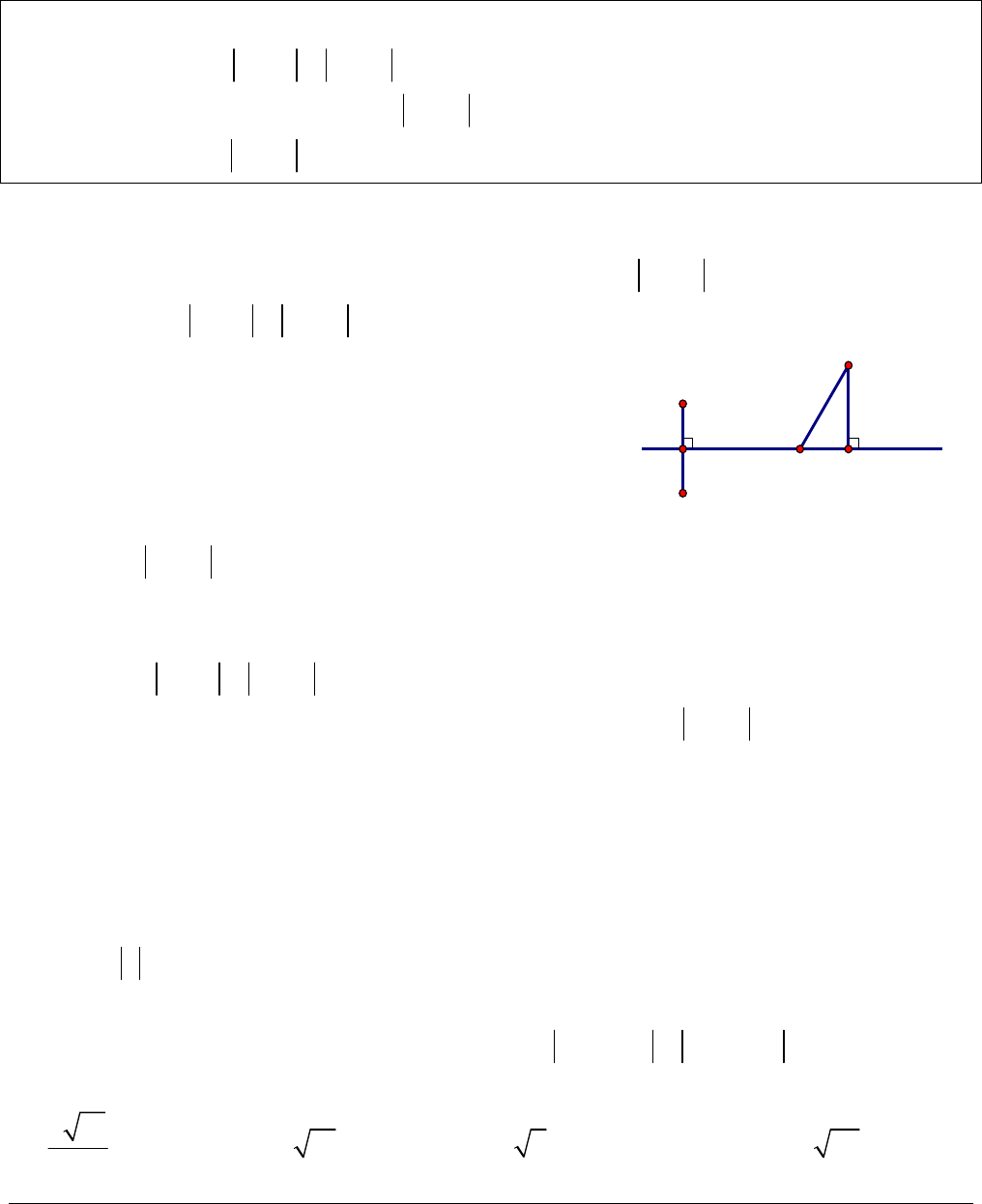Trang 3 2. Các bài toán BÀI TOÁN 1:Cho số phức 000,,zab iab và tập hợp các số phức zxyi thỏa mãn hệ thức: 12.zzzz a) Tìm giá trị nhỏ nhất của 0zz b) Tìm z để 0zz nhỏ nhất Nhận xét: + Gọi ()MMz, 00012();();()MMzAAzBBz thì 00zzMM + Từ đẳng thức 12.zzzz Suy ra, M thuộc trung trực  của đoạn AB. Bài toán chuyển thành: a) Tìm giá trị nhỏ nhất của 0MM với .M  b) Tìm M  sao cho 0MM nhỏ nhất + Ta thấy, với mọi điểm M  thì 00,MMMH trong đó H là hình chiếu của M0 lên . Do đó, 00min(;).zzdM Và để 0MM nhỏ nhất với M  thì MH hay M là hình chiếu của M0 lên . Lời giải - Từ hệ thức 12zzzz, suy ra phương trình đường thẳng . + Với câu a), ta tính khoảng cách 0(;).dM Và kết luận, 00min(;).zzdM + Với câu b), - Viết phương trình đường thẳng d đi qua M0, vuông góc với  (hoặc song song với ).AB - Giải hệ gồm hai phương trình:  và d suy ra nghiệm (;).xy Kết luận, số phức cần tìm là .zxyi Đặc biệt: minz tức là tìm số phức z sao cho mô đun của z là nhỏ nhất. Ví dụ 1.1. Trong tất cả các số phức z thỏa mãn 1234.zizi Tìm giá trị nhỏ nhất của mô đun của .z A. 51313 B. 213 C. 2 D. 26 ΔA(z1)B(z2)M0HM Chia sẻ bởi: Trịnh Thị Thanh

Tải về

Liên kết tải về Giải bài toán cực trị số phức bằng phương pháp hình học giải tích 396,8 KB Tải về Tìm thêm: Toán 12

Có thể bạn quan tâm

• 

  Cảm nghĩ về tác phẩm Cây tre Việt Nam của Thép Mới

  10.000+
• 

  Bộ đề thi học kì 2 môn Lịch sử 11 năm 2024 - 2025 (Sách mới)

  50.000+
• 

  Bộ đề thi học kì 2 môn Tiếng Anh 7 năm 2024 - 2025 (Sách mới)

  100.000+ 1
• 

  Tổng hợp kết bài Những ngôi sao xa xôi (56 mẫu)

  100.000+
• 

  Bộ đề thi học kì 2 môn Ngữ văn lớp 10 năm 2024 - 2025 (Sách mới)

  100.000+
• 

  Văn mẫu lớp 8: Thuyết minh về cuốn sách Ngữ văn 8 tập 2

  50.000+ 1
• 

  Bài thơ Sóng - In trong tập Hoa dọc chiến hào (1968)

  100.000+
• 

  Văn mẫu lớp 9: Nghị luận xã hội Lá lành đùm lá rách

  100.000+
• 

  Đoạn văn tiếng Anh về ưu điểm của việc tự học (4 Mẫu)

  10.000+
• 

  GDCD 6 Bài 2: Yêu thương con người

  10.000+

Xem thêm

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Khiếu nại & Hoàn tiền

Giải quyết vấn đề đơn hàng & hoàn trả

Mới nhất trong tuần

• Sơ đồ tư duy môn Toán 12 (Cả năm, Chương trình mới)

  

• Các dạng bài tập cực trị của hàm số

  

• Tài liệu ôn thi Toán lớp 12

  

• Bộ đề thi chọn học sinh giỏi môn Toán lớp 12 (Cấu trúc mới)

  

• Tóm tắt lý thuyết và giải nhanh Toán 12

  

• Các dạng bài tập tính đơn điệu của hàm số

  

• Đề thi thử THPT Quốc gia năm 2025 môn Ngữ văn trường THPT Yên Dũng 2, Bắc Giang

  

• 524 câu hỏi vận dụng cao trong các đề thi THPT Quốc gia

  

• Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 năm 2023 - 2024

  

• Lý thuyết và bài tập trắc nghiệm số phức

  

Đóng Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ Nhắn tin Zalo

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2025 download.vn.