Giải Pt Dạng Asinx Bcosx =c - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
Nhi Trần 9 tháng 6 2021 lúc 14:02 Giải pt dạng asinx+bcosx =c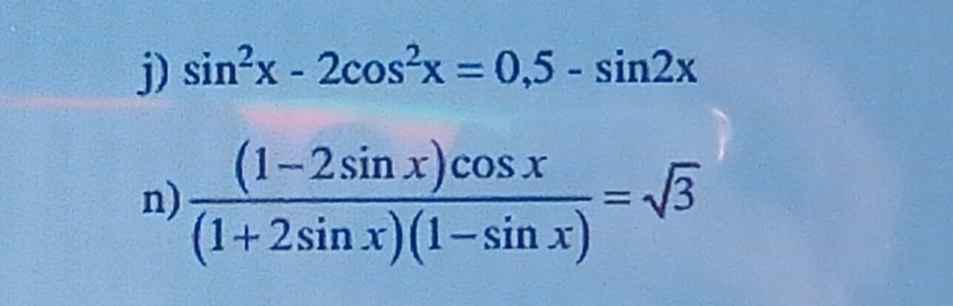
- Nhi Trần
Giải pt dạng asinx+bcosx=c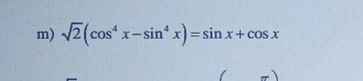
Gửi Hủy 
Lê Thị Thục Hiền 
15 tháng 6 2021 lúc 10:48 \(\sqrt{2}\left(cos^4x-sin^4x\right)=sinx+cosx\)
\(\Leftrightarrow\sqrt{2}\left(cos^2x+sin^2x\right)\left(cosx-sinx\right)\left(cosx+sinx\right)=sinx+cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left[\sqrt{2}\left(cosx-sinx\right)-1\right]=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\left[2cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=k\pi\\x+\dfrac{\pi}{4}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{4}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k2\pi\\x=-\dfrac{7\pi}{12}+k2\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
Đúng 2 Bình luận (0) Gửi Hủy - Nhi Trần
Giải Pt dạng asinx+bcosx=c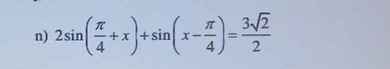
Gửi Hủy 
Akai Haruma Giáo viên 15 tháng 6 2021 lúc 0:11 Lời giải:PT \(\Leftrightarrow 2(\sin \frac{\pi}{4}\cos x+\cos \frac{\pi}{4}\sin x)+(\sin x\cos \frac{\pi}{4}-\cos x\sin \frac{\pi}{4})=\frac{3\sqrt{2}}{2}\)
\(\Leftrightarrow \sqrt{2}(\cos x+\sin x)+\frac{\sqrt{2}}{2}(\sin x-\cos x)=\frac{3\sqrt{2}}{2}\)
\(\Leftrightarrow 2(\cos x+\sin x)+(\sin x-\cos x)=3\)
\(\Leftrightarrow \cos x+3\sin x=3\)
\(\Leftrightarrow \frac{1}{\sqrt{10}}\cos x+\frac{3}{\sqrt{10}}\sin x=\frac{3}{\sqrt{10}}\)
\(\Leftrightarrow \sin t\cos x+\cos t\sin x=\cos t\) với \(\frac{1}{\sqrt{10}}=\sin t(t\in (0;\pi))\)
\(\Leftrightarrow \sin (t+x)=\cos t=\sin (\frac{\pi}{2}-t)\)
\(\Rightarrow t+x=\frac{\pi}{2}-t+2k\pi\) hoặc $t+x=\frac{\pi}{2}+t+2k\pi$ với $k$ nguyên.
Đúng 0 Bình luận (0)
Gửi Hủy - Nhi Trần
Giải pt asinx + bcosx =c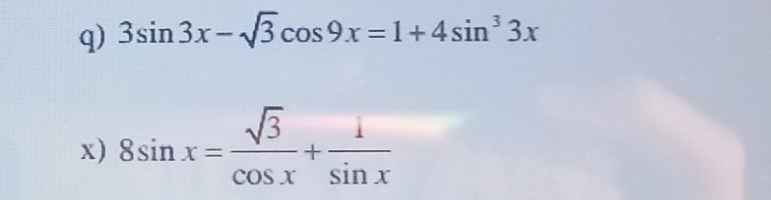
Gửi Hủy Lê Thị Thục Hiền 15 tháng 6 2021 lúc 15:09 q) \(3sin3x-\sqrt{3}cos9x=1+4sin^33x\)
\(\Leftrightarrow3sin3x-\sqrt{3}cos9x=1+3sin3x-sin9x\)
\(\Leftrightarrow sin9x-\sqrt{3}cos9x=1\)
\(\Leftrightarrow sin9x.cos\dfrac{\pi}{3}-cos9x.sin\dfrac{\pi}{3}=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(9x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+\dfrac{k2\pi}{9}\\x=\dfrac{7\pi}{54}+\dfrac{k2\pi}{9}\end{matrix}\right.\) (\(k\in Z\))
Vậy...
x) \(8sinx=\dfrac{\sqrt{3}}{cosx}+\dfrac{1}{sinx}\)
(đk: \(cosx\ne0;sinx\ne0\) \(\Rightarrow sin2x\ne0\) \(\Leftrightarrow x\ne\dfrac{k\pi}{2}\);\(k\in Z\))
\(\Leftrightarrow8sinx=\dfrac{\sqrt{3}sinx+cosx}{cosx.sinx}\)
\(\Leftrightarrow\)\(8sinx.cosx.sinx=\sqrt{3}sinx+cosx\)
\(\Leftrightarrow4sinx.sin2x=\sqrt{3}sinx+cosx\)
\(\Leftrightarrow2\left(cosx-cos3x\right)=\sqrt{3}sinx+cosx\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=2cos3x\)
\(\Leftrightarrow cosx.cos\left(\dfrac{\pi}{3}\right)-sinx.sin\left(\dfrac{\pi}{3}\right)=cos3x\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos3x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}-k\pi\\x=-\dfrac{\pi}{12}+\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\)) (thỏa mãn)
Vậy...
Đúng 1 Bình luận (2) Gửi Hủy - Nhi Trần
giải pt asinx + bcosx = c
Gửi Hủy Lê Thị Thục Hiền 9 tháng 6 2021 lúc 14:38 Pt \(\Leftrightarrow\dfrac{3}{5}sin\left(x+1\right)+\dfrac{4}{5}cos\left(x+1\right)=1\)
Đặt \(cos\alpha=\dfrac{3}{5}\Rightarrow sin\alpha=\dfrac{4}{5}\) ( vì \(cos^2\alpha+sin^2\alpha=1\))
Pt tt: \(sin\left(x+1\right).cos\alpha+cos\left(x+1\right).sin\alpha=1\)
\(\Leftrightarrow sin\left(x+1+\alpha\right)=1\)
\(\Leftrightarrow x+1+\alpha=\dfrac{\pi}{2}+k2\pi\) (\(k\in Z\))
\(\Leftrightarrow x=\dfrac{\pi}{2}-\alpha-1+k2\pi\) (\(k\in Z\))
Đúng 1 Bình luận (0) Gửi Hủy 
Trần Ái Linh 
9 tháng 6 2021 lúc 14:41 `3sin(x+1)+4cos(x+1)=5`
`<=> 3/5 sin(x+1) + 4/5 cos (x+1)=1`
Vì `(3/5)^2 + (4/5)^2 = 1` nên ta có:
Đặt \(\left\{{}\begin{matrix}sinα=\dfrac{3}{5}\\cosα=\dfrac{4}{5}\end{matrix}\right.\)
`sin α . sin(x+1)+cosa . cos(x+1)=1`
`<=> cos(α - x-1)=1`
`<=> α -x-1=k2π`
`<=> x=α-1+k2α (k \in ZZ)`
Đúng 1 Bình luận (0)
Gửi Hủy 
- Pham Trong Bach
Nêu cách giải phương trình lượng giác cơ bản , cách giải phương trình a sin x + b cos x = c .
Xem chi tiết Lớp 11 Toán 1 0 Gửi Hủy 
Cao Minh Tâm 
2 tháng 11 2017 lúc 3:05 a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: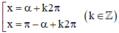 
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho 
ta được:
Ta giải phương trình trên như phương trình lượng giác cơ bản.
Đúng 0 Bình luận (0) Gửi Hủy - Nhi Trần
giải pt dạng asinx + bscosx = c câu g,h,j
Gửi Hủy Lê Thị Thục Hiền 10 tháng 6 2021 lúc 17:01 g)\(5sin2x-6cos^2x=13\)
\(\Leftrightarrow10.sinx.cosx-6cos^2x=13\left(sin^2x+cos^2x\right)\)
\(\Leftrightarrow13.sin^2x-10.sinx.cosx+19.cos^2x=0\)
\(\Leftrightarrow13\left(sinx-\dfrac{5}{13}cosx\right)^2+\dfrac{222}{13}cos^2x=0\) (vô nghiệm vì dấu bằng xảy ra khi sinx=cosx=0 \(\Rightarrow∄x\))
Vậy pt vô nghiệm
h)\(cos^2x+2\sqrt{3}sinx.cosx+3sin^2x=1\)
\(\Leftrightarrow1+2sin^2x+2\sqrt{3}.sinx.cosx=1\)
\(\Leftrightarrow2sinx\left(sinx+\sqrt{3}cosx\right)=0\)
\(\Leftrightarrow2.sinx.2sin\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sin\left(x+\dfrac{\pi}{3}\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)(k nguyên)
Vậy...
j) \(sinx+cosx=\sqrt{2}.sin4x\)
\(\Leftrightarrow sinx.\dfrac{1}{\sqrt{2}}+cosx.\dfrac{1}{\sqrt{2}}=sin4x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin4x\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=4x+k2\pi\\x+\dfrac{\pi}{4}=\pi-4x+k2\pi\end{matrix}\right.\)(\(k\in Z\))\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}-\dfrac{k2\pi}{3}\\x=\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
Đúng 2 Bình luận (0) Gửi Hủy - Pham Trong Bach
Tìm điều kiện cần và đủ của a, b, c để phương trình asinx+bcosx=c có nghiệm
Gửi Hủy Cao Minh Tâm 4 tháng 12 2017 lúc 10:47 
Gửi Hủy - Pham Trong Bach
Tìm điều kiện cần và đủ của a, b, c để phương trình a sin x + b cos x = c có nghiệm?
A. a 2 + b 2 > c 2
B. a 2 + b 2 ≤ c 2
C. a 2 + b 2 = c 2
D. a 2 + b 2 ≥ c 2
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy Cao Minh Tâm 22 tháng 8 2017 lúc 9:17 Chọn D.
Phương pháp:
Phương trình thuần nhất đối với sin và cos, dạng
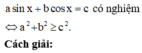
Phương trình thuần nhất đối với sin và cos, dạng
Gửi Hủy 
- Quỳnh Anh
Tìm GTLN, GTNN của các biểu thức sau
1, \(A=sinx-cosx\)
2, \(B=sinx=cosx\)
3, \(C=asinx-bcosx\)
4, \(D=sin^4x-cos^4x\)
Xem chi tiết Lớp 10 Toán Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG... 1 0 Gửi Hủy 
Nguyễn Việt Lâm CTV 
17 tháng 4 2021 lúc 11:38 \(A=\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)\Rightarrow-\sqrt{2}\le A\le\sqrt{2}\)
B ko rõ đề
\(C=\sqrt{a^2+b^2}\left(\dfrac{a}{\sqrt{a^2+b^2}}sinx-\dfrac{b}{\sqrt{a^2+b^2}}cosx\right)\)
Đặt \(\dfrac{a}{\sqrt{a^2+b^2}}=cosy\Rightarrow\dfrac{b}{\sqrt{a^2+b^2}}=siny\)
\(\Rightarrow C=\sqrt{a^2+b^2}\left(sinx.cosy-cosx.siny\right)=\sqrt{a^2+b^2}sin\left(x-y\right)\)
\(\Rightarrow-\sqrt{a^2+b^2}\le C\le\sqrt{a^2+b^2}\)
\(D=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)=sin^2x-cos^2x=-cos2x\)
\(\Rightarrow-1\le D\le1\)
Đúng 0 Bình luận (0) Gửi Hủy Khoá học trên OLM (olm.vn)
- Toán lớp 11 (Kết nối tri thức với cuộc sống)
- Toán lớp 11 (Cánh Diều)
- Toán lớp 11 (Chân trời sáng tạo)
- Ngữ văn lớp 11
- Tiếng Anh lớp 11 (i-Learn Smart World)
- Tiếng Anh lớp 11 (Global Success)
- Vật lý lớp 11 (Kết nối tri thức với cuộc sống)
- Vật lý lớp 11 (Cánh diều)
- Hoá học lớp 11 (Kết nối tri thức với cuộc sống)
- Hoá học lớp 11 (Cánh diều)
- Sinh học lớp 11 (Kết nối tri thức với cuộc sống)
- Sinh học lớp 11 (Cánh diều)
- Lịch sử lớp 11 (Kết nối tri thức với cuộc sống)
- Lịch sử lớp 11 (Cánh diều)
- Địa lý lớp 11 (Kết nối tri thức với cuộc sống)
- Địa lý lớp 11 (Cánh diều)
- Giáo dục kinh tế và pháp luật lớp 11 (Kết nối tri thức với cuộc sống)
- Tin học lớp 11 (Kết nối tri thức với cuộc sống)
- Công nghệ lớp 11 (Kết nối tri thức với cuộc sống)
Từ khóa » Giải Phương Trình Lượng Giác Dạng Asinx+bcosx=c
-
Phương Trình Asinx + Bcosx = C
-
Nêu Cách Giải Phương Trình Lượng Giác Cơ Bản , Cách ... - Khóa Học
-
Bài Giảng Số 2: Phương Trình Lượng Giác Dạng ... - Bài Giảng Toán Học
-
Tìm Điều Kiện Có Nghiệm Của Phương Trình Lượng Giác Asinx ...
-
Cách Giải PT Lượng Giác: Asinx + Bcosx = C (Siêu Nhanh) - YouTube
-
Phương Trình Lượng Giác Dạng Asinx+bcosx=c - YouTube
-
Bài 9: Phương Trình Asinx + Bcosx = C - YouTube
-
Một Số Dạng Phương Trình Lượng Giác Thường Gặp - Baitap123
-
Phương Trình đưa Về Dạng Asinx + Bcosx = C
-
Lý Thuyết Giải Các Phương Trình Lượng Giác Cơ Bản Thường Gặp
-
Bài Giảng Số 2: Phương Trình Lượng Giác Dạng Asinx + ... - 123doc
-
Tổng Hợp Các Dạng Phương Trình Lượng Giác Thường Gặp
-
"Mục Sở Thị" Cách Giải Chuyên đề Phương Trình Lượng Giác Lớp 11 ...
-
Giáo án Tự Chọn 11 - Tiết 7: Phương Trình Asinx + Bcosx = C