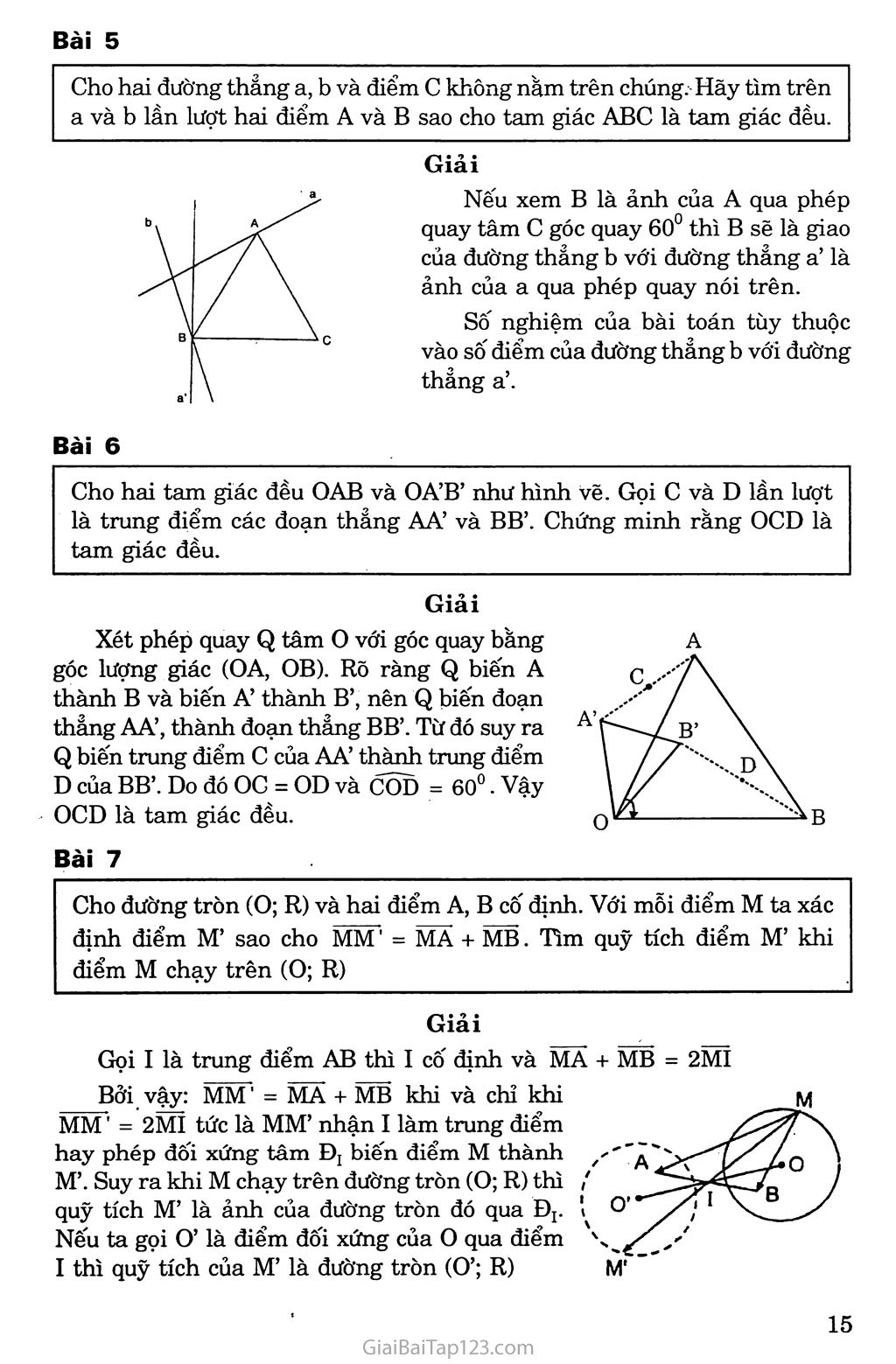
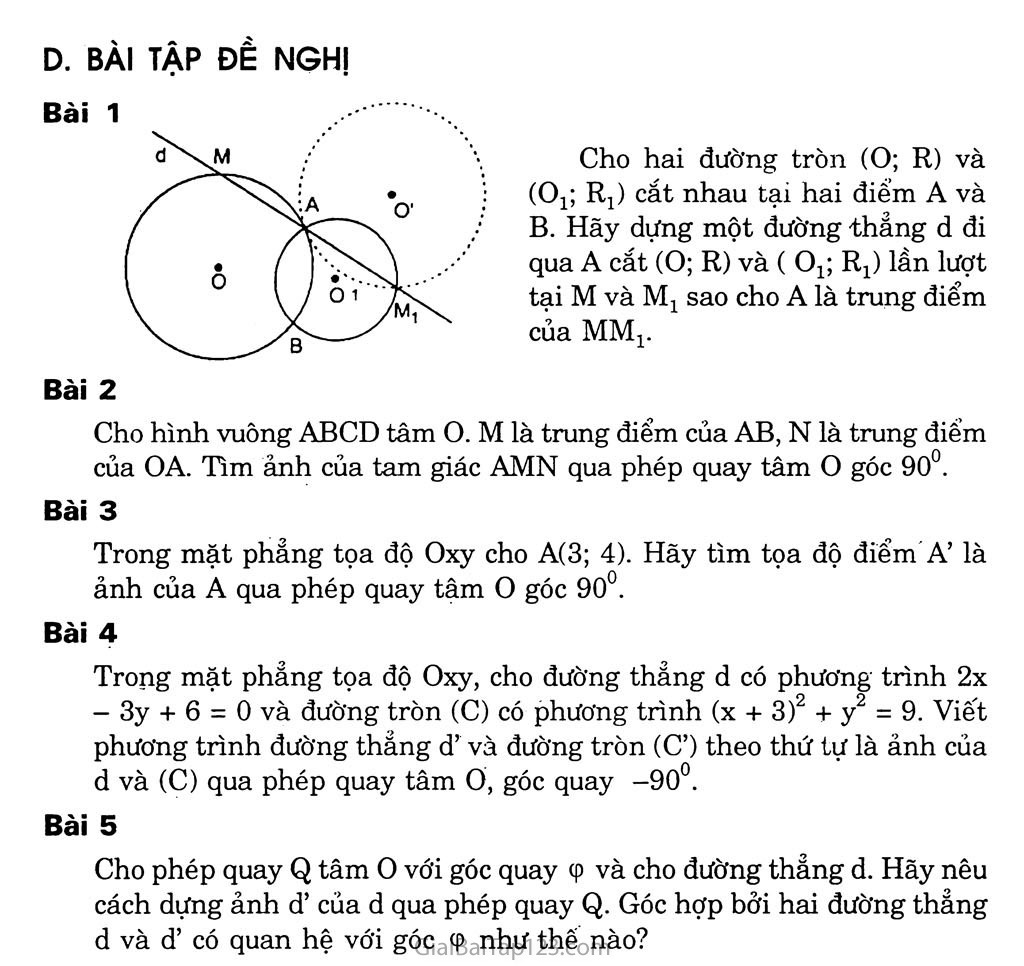
Giải Toán 11: Vấn đề 2. Phép Quay

• Home
• Lớp 1,2,3
  • Lớp 1
  • Giải Toán Lớp 1
  • Tiếng Việt Lớp 1
  • Lớp 2
  • Giải Toán Lớp 2
  • Tiếng Việt Lớp 2
  • Văn Mẫu Lớp 2
  • Lớp 3
  • Giải Toán Lớp 3
  • Tiếng Việt Lớp 3
  • Văn Mẫu Lớp 3
  • Giải Tiếng Anh Lớp 3
• Lớp 4
  • Giải Toán Lớp 4
  • Tiếng Việt Lớp 4
  • Văn Mẫu Lớp 4
  • Giải Tiếng Anh Lớp 4
• Lớp 5
  • Giải Toán Lớp 5
  • Tiếng Việt Lớp 5
  • Văn Mẫu Lớp 5
  • Giải Tiếng Anh Lớp 5
• Lớp 6
  • Soạn Văn 6
  • Giải Toán Lớp 6
  • Giải Vật Lý 6
  • Giải Sinh Học 6
  • Giải Tiếng Anh Lớp 6
  • Giải Lịch Sử 6
  • Giải Địa Lý Lớp 6
  • Giải GDCD Lớp 6
• Lớp 7
  • Soạn Văn 7
  • Giải Bài Tập Toán Lớp 7
  • Giải Vật Lý 7
  • Giải Sinh Học 7
  • Giải Tiếng Anh Lớp 7
  • Giải Lịch Sử 7
  • Giải Địa Lý Lớp 7
  • Giải GDCD Lớp 7
• Lớp 8
  • Soạn Văn 8
  • Giải Bài Tập Toán 8
  • Giải Vật Lý 8
  • Giải Bài Tập Hóa 8
  • Giải Sinh Học 8
  • Giải Tiếng Anh Lớp 8
  • Giải Lịch Sử 8
  • Giải Địa Lý Lớp 8
• Lớp 9
  • Soạn Văn 9
  • Giải Bài Tập Toán 9
  • Giải Vật Lý 9
  • Giải Bài Tập Hóa 9
  • Giải Sinh Học 9
  • Giải Tiếng Anh Lớp 9
  • Giải Lịch Sử 9
  • Giải Địa Lý Lớp 9
• Lớp 10
  • Soạn Văn 10
  • Giải Bài Tập Toán 10
  • Giải Vật Lý 10
  • Giải Bài Tập Hóa 10
  • Giải Sinh Học 10
  • Giải Tiếng Anh Lớp 10
  • Giải Lịch Sử 10
  • Giải Địa Lý Lớp 10
• Lớp 11
  • Soạn Văn 11
  • Giải Bài Tập Toán 11
  • Giải Vật Lý 11
  • Giải Bài Tập Hóa 11
  • Giải Sinh Học 11
  • Giải Tiếng Anh Lớp 11
  • Giải Lịch Sử 11
  • Giải Địa Lý Lớp 11
• Lớp 12
  • Soạn Văn 12
  • Giải Bài Tập Toán 12
  • Giải Vật Lý 12
  • Giải Bài Tập Hóa 12
  • Giải Sinh Học 12
  • Giải Tiếng Anh Lớp 12
  • Giải Lịch Sử 12
  • Giải Địa Lý Lớp 12

Trang Chủ › Lớp 11› Giải Bài Tập Toán 11› Giải Toán 11 Hình Học› Vấn đề 2. Phép quay Giải Toán 11: Vấn đề 2. Phép quay

• 
• 
• 
• 
• 
• 

(Vấn đề 2. PHEP QUAY A. KIẾN THỨC CẦN NHỚ ĐỊNH NGHĨA Cho điểm I cố định và một góc lượng giác a . Phép quay tâm I góc a , kí hiệu là Q“ , là phép biến hình biến mỗi điểm M thành một điểm M’ xác định, sao cho IM’ = IM và góc lượng giác (IM; IM’) bằng a . Điểm I được gọi là tâm quay, góc a được gọi là góc quay Phép quay hoàn toàn được xác định khi biết tâm và góc quay của nó. . CHÚ Ý Chiều dương í ’’.a phép quay trùng với chiều dương của đường tròn lượng giác. Với mọi số k nguyên phép quay Q2k' là phép đồng nhất và phép quay Q,I2k+ll:tlà phép đối xứng tâm I. n. TÍNH CHẤT Định lí Phép quay bảo toàn khoảng cách giữa hai điểm bất kì. Hệ quả Hệ quả 1 Phép quay biến ba điểm A, B, c thẳng hàng với B nằm giữa A và c tương ứng thành ba điểm A’, B’, C’ thẳng hàng với B’ nằm giữa A’ và C’. Hệ quả 2 Phép quay Biến đường thẳng thành đường thẳng, Biến tam giác thành tam giác bằng tam giác đã cho, Biến đường tròn thành đường tròn có bán kính bằng bán kính đường tròn đã cho, trong đó tâm đường trồn biến thành tâm đường tròn. B. GIẢI BÀI TẬP SÁCH GIÁO KHOA Bài 1 Cho hình vuông ABCD tâm 0 D c a) Tìm ảnh của điểm c qua phép quay tâm A góc 90°. V b) Tìm ảnh của đường thẳng BC qua phép quay tâm 0 góc 90°. t z\ Giải Gọi E là điểm đối xứng với c qua tâm D. Khi đó <3 „ (C) = E. (A,90°) Q,„ = c, <3 „ (C) = D. Vậy ảnh của đường thảng BC qua phép quay tâm o góc 90° là đường thẳng CD. Bài 2 Trong mặt phảng tọa độ Oxy cho điểm A(2; 0) và đường thẳng d có phương trình X + y - 2 = 0. Tìm ảnh của A và d qua phép quay tâm o góc 90°. Giải Gọi B là ảnh của A. Khi đó B = (0; 2). A và B(0; 2) thuộc d. Ảnh của B qua phép tâm quay tâm o góc 90° là A’(-2; 0). Do đó ảnh của d qua phép quay tâm o góc 90° là đường thẳng BA’ có phương trình BÀI TẬP BỔ SUNG Bài 1 Hãy chỉ ra phép quay (không phải phép đồng nhất) Biến hình chữ nhật thành chính nó, Biến ngũ giác đều thành chính nó, Biến hyperbol X2 - 2y2 = 2 thành chính nó. Giải Gọi I là tâm của hình chữ nhật. Khi đó phép quay (với k nguyên tùy ý) sẽ biến hình chữ nhật thành chính nó. 2 Gọi o là tâm của ngũ giác đều. Khi đó phép quay Qo 5 (với k nguyên tùy ý) sẽ biến hình ngũ giác đều thành chính nó. Vẽ hyperbol trên hệ trục tọa độ Oxy. ta thấy phép quay Qo" (với k nguyên tùy ý) sẽ biến hyperbol X2 - 2y =2 thành chính nó. Bài 2 Cho hai đường tròn tâm o và tâm O’ có bán kính bằng nhau. Hãy chỉ ra một phép quay biến đường tròn này thành đường tròn kia. Giải Lấy điểm I cố định trên trục đối xứng d của đoạn.00’. Phép quay tâm I góc a (là góc lượng giác giữa hai tia 10 và 10’) biến đường tròn (O) thành đường tròn (O’). Bài 3 Cho đường tròn tâm o, bán kính R. Lấy một điểm M trên đường tròn. Gọi M’ là ảnh của M qua phép quay tâm o góc 30° và M” là ảnh của M’ qua phép đối xứng qua đường thẳng OM. Chứng minh rằng 0M’M” là tam giác đều. Giải Do Qq°° biến M thầnh M’ nên góc lượng giác (OM, OM’) bằng 30° hay MỒM' = 30° Lại do Đom biến M’ thành M” nên OM’ = OM” hay AOM' M" là tam giác cân. Từ đó suy ra là AOM'M" là tam giác đều. Bài 4 Cho tam giác ABC. Dựng về phía ngoài của tam giác đó các hình vuông ABMN và ACPQ. Gọi I là trung điểm của BC, Oi và 02 lần lượt là tâm của các hình vuông ABMN và ACPQ. Chứng minh rằng 10^2 là tam giác vuông cân tại I. Chứng minh rằng AI vuông góc với NQ và AI = NQ. Giải Gọi f là phép quay tâm A góc quay 90°. Khi đó f biến đoạn thẳng NC thành đoạn thẳng BQ. Do đó hai đoạn thẳng ấy bằng nhau và vuông góc với nhau. Vì 0J song song và bằng nửa NC, 02I song song và bằng nửa BQ nên 0J và 02I bằng nhau và vuông góc với nhau. E Gọi E là điểm đối xứng với B qua A. Khi đó f biến đoạn thẳng EC thành đoạn thảng NQ. Do đó hai đoạn thẳng ấy bằng nhau và vuông gỏc với nhau. Ta thấy rằng AI song song và bằng nửa CE ta sẽ suy ra điều phải chứng minh. Bài 5 Cho hai đường thẳng a, b và điểm c không nằm trên chúng. Hãy tìm trên a và b lần lượt hai điểm A và B sao cho tam giác ABC là tam giác đều. Giải Nếu xem B là ảnh của A qua phép quay tâm c góc quay 60° thì B sẽ là giao của đường thẳng b với đường thẳng a’ là ảnh của a qua phép quay nói trên. Sô' nghiệm của bài toán tùy thuộc vào số điểm của đường thẳng b với đường thẳng a’. Cho hai tam giác đều OAB và OA’B’ như hình vẽ. Gọi c và D lần lượt là trung điểm các đoạn thẳng AA’ và BB’. Chứng minh rằng OCD là tam giác đều. Giải Xét phép quay Q tâm o với góc quay bằng góc lượng giác (OA, OB). Rõ ràng Q biến A thành B và biến A’ thành B’, nên Q biến đoạn thẳng AA’, thành đoạn thẳng BB’. Từ đó suy ra Q biến trung điểm c của AA’ thành trung điểm D của BB’. Do đó oc = OD và COD = 60°. Vậy OCD là tam giác đều. Bài 7 Cho đường tròn (O; R) và hai điểm A, B cố định. Với mỗi điểm M ta xác định điểm M’ sao cho MM ’ = MA + MB. Tìm quỹ tích điểm M’ khi điểm M chạy trên (O; R) Giải Gọi I là trung điểm AB thì I cố định và MA + MB = 2MI Bởi vậy: MM' = MA + MB khi và chỉ khi MM' = 2MI tức là MM’ nhận I làm trung điểm hay phép đối xứng tâm Đj biến điểm M thành M’. Suy ra khi M chạy trên đường tròn (O; R) thì quỹ tích M’ là ảnh của đường tròn đó qua Đj. Nếu ta gọi O’ là điểm đối xứng của o qua điểm I thì quỹ tích của M’ là đường tròn (O’; R) D. BẢI TẬP ĐẼ NGHỊ Cho hai đường tròn (O; R) và : (Ox; Rj) cắt nhau tại hai điếm A và B. Hãy dựng một đường thẳng d đi qua A cắt (O; R) và ( Op RJ lần lượt tại M và Mx sao cho A là trung điểm cua MMp Cho hình vuông ABCD tâm o. M là trung điểm của AB, N là trung điểm của OA. Tìm ảnh của tam giác AMN qua phép quay tâm o góc 90°. Bài 3 Trong mặt phảng tọa độ Oxy cho A(3; 4). Hãy tìm tọa độ điểm A’ là ảnh của A qua phép quay tâm o góc 90°. Bài 4 Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình 2x - 3y + 6 = 0 và đường tròn (C) có phương trình (x + 3)2 + y2 = 9. Viết phương trình đường thẳng d’ và đường tròn (ơ) theo thứ tự là ảnh của d và (C) qua phép quay tâm 0, góc quay -90°. Bài 5 Cho phép quay Q tâm 0 với góc quay <p và cho đường thẳng d. Hãy nêu cách dựng ảnh d’ của d qua phép quay Q. Góc hợp bởi hai đường thẳng d và d’ có quan hệ với góc (p như thể nào?

Các bài học tiếp theo

• Vấn đề 3. Khái niệm về phép dời hình và hai hình bằng nhau
• Vấn đề 4. Phép vị tự
• Vấn đề 5. Phép đồng dạng
• Bài tập ôn chương I
• Vấn đề 1. Đại cương về đường thẳng và mặt phẳng
• Vấn đề 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
• Vấn đề 3. Đường thẳng song song mặt phẳng
• Vấn đề 4. Hai mặt phẳng song song
• Bài tập ôn chương II
• Vấn đề 1. Vectơ trong không gian

Các bài học trước

• Vấn đề 1. Phép tịnh tiến

Tham Khảo Thêm

• Sách Giáo Khoa - Đại Số và Giải Tích 11
• Sách Giáo Khoa - Hình Học 11
• Giải Bài Tập Toán 11 Đại Số
• Giải Bài Tập Toán 11 Hình Học
• Giải Toán 11 Đại Số và Giải Tích
• Giải Toán 11 Hình Học(Đang xem)
• Giải bài tập Đại số và Giải tích 11
• Giải bài tập Hình học 11

Giải Toán 11 Hình Học

• Chương I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
• Vấn đề 1. Phép tịnh tiến
• Vấn đề 2. Phép quay(Đang xem)
• Vấn đề 3. Khái niệm về phép dời hình và hai hình bằng nhau
• Vấn đề 4. Phép vị tự
• Vấn đề 5. Phép đồng dạng
• Bài tập ôn chương I
• Chương II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN - QUAN HỆ SONG SONG
• Vấn đề 1. Đại cương về đường thẳng và mặt phẳng
• Vấn đề 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
• Vấn đề 3. Đường thẳng song song mặt phẳng
• Vấn đề 4. Hai mặt phẳng song song
• Bài tập ôn chương II
• Chương III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
• Vấn đề 1. Vectơ trong không gian
• Vấn đề 2. Hai đường thẳng vuông góc
• Vấn đề 3. Đường thẳng vuông góc với mặt phẳng
• Vấn đề 4. Hai mặt phẳng vuông góc
• Vấn đề 5. Khoảng cách
• Bài tập ôn chương III
• Bài tập trắc nghiệm chương III
• Bài tập ôn tập cuối năm